Difference between revisions of "Rayleigh-Bloch Waves"
| (13 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | Rayleigh | + | Rayleigh-Bloch waves are waves which travel along an |
| − | supported by the structure) will be excited in a [[Semi-Infinite Array]] provided that <math>k < \pi/R</math> (where <math>k</math> is the wavenumber of the incident wave and <math>R</math> is the body spacing of the array). | + | [[:Category:Infinite Array|Infinite Array]]. |
| + | Generally, they propagate along the array with a dominant wavenumber which is greater than that for freely-propagating waves and they decay exponentially away from the array. They have other names (guided waves, surface waves) in acoustics and electromagnetics. Only in very exceptional cases are they excited by plane incident waves ([[Porter and Evans 2005]]). Rayleigh-Bloch waves (if they can be supported by the structure) will be excited in a [[Semi-Infinite Array]] provided that <math> \ k < \pi/R \ </math> (where <math>k</math> is the wavenumber of the incident wave and <math>R</math> is the body spacing of the array). | ||
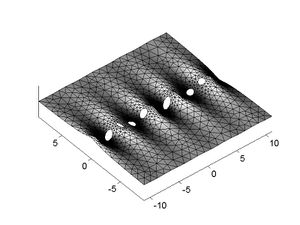
| − | + | [[Image:RB_wiki.jpg|thumb|right|Rayleigh-Bloch wave travelling down an infinite array of bottom-mounted cylinders]] | |
| − | |||
| − | The Rayleigh--Bloch wavenumber <math>\beta</math> is the value for which the operator | + | Rayleigh-Bloch waves are observed for a very general class of arrays, where the medium is governed by the two-dimensional [[Helmholtz's Equation]] (cf. [[Linton and McIver 2002]]). In the water-wave context this means that the structures must have a depth dependence which can be removed (cf. [[Removing The Depth Dependence]]), so that the problem reduces to two dimensions. In the more general water-wave context, no Rayleigh-Bloch waves have been found (see [[Peter and Meylan 2007]] for a discussion). It seems likely that such waves will exist only for very special geometries and frequencies, but this remains only a conjecture at the present time. There are many off-shore structures which do support Rayleigh-Bloch waves, e.g. [[Bottom Mounted Cylinder|Bottom-Mounted Cylinders]]. |
| + | Some more information on Rayleigh--Bloch waves can be found in [[Porter and Evans 1999]] and [[Linton and McIver 2002]]. | ||
| + | |||
| + | The Rayleigh-Bloch wavenumber <math>\beta</math> is the value for which the operator | ||
<math>-\nabla^2</math>, subject to the periodicity conditions | <math>-\nabla^2</math>, subject to the periodicity conditions | ||
| Line 14: | Line 17: | ||
and appropriate boundary conditions at the body surfaces, has an | and appropriate boundary conditions at the body surfaces, has an | ||
| − | eigenvalue in the interval <math>(k,\pi/R]</math>. This corresponds to a wave | + | eigenvalue in the interval <math> \ (k,\pi/R] \ </math>. This corresponds to a wave |
travelling down the array with phase factor | travelling down the array with phase factor | ||
<math> | <math> | ||
| − | + | \ Q_j = \mathrm{e}^{\mathrm{i} j R \beta}. | |
</math> | </math> | ||
| + | |||
| + | An example is given in the plot. | ||
| + | |||
| + | [[Category:Infinite Array]] | ||
Latest revision as of 11:37, 23 September 2010
Rayleigh-Bloch waves are waves which travel along an Infinite Array. Generally, they propagate along the array with a dominant wavenumber which is greater than that for freely-propagating waves and they decay exponentially away from the array. They have other names (guided waves, surface waves) in acoustics and electromagnetics. Only in very exceptional cases are they excited by plane incident waves (Porter and Evans 2005). Rayleigh-Bloch waves (if they can be supported by the structure) will be excited in a Semi-Infinite Array provided that [math]\displaystyle{ \ k \lt \pi/R \ }[/math] (where [math]\displaystyle{ k }[/math] is the wavenumber of the incident wave and [math]\displaystyle{ R }[/math] is the body spacing of the array).
Rayleigh-Bloch waves are observed for a very general class of arrays, where the medium is governed by the two-dimensional Helmholtz's Equation (cf. Linton and McIver 2002). In the water-wave context this means that the structures must have a depth dependence which can be removed (cf. Removing The Depth Dependence), so that the problem reduces to two dimensions. In the more general water-wave context, no Rayleigh-Bloch waves have been found (see Peter and Meylan 2007 for a discussion). It seems likely that such waves will exist only for very special geometries and frequencies, but this remains only a conjecture at the present time. There are many off-shore structures which do support Rayleigh-Bloch waves, e.g. Bottom-Mounted Cylinders. Some more information on Rayleigh--Bloch waves can be found in Porter and Evans 1999 and Linton and McIver 2002.
The Rayleigh-Bloch wavenumber [math]\displaystyle{ \beta }[/math] is the value for which the operator [math]\displaystyle{ -\nabla^2 }[/math], subject to the periodicity conditions
[math]\displaystyle{ \phi|_{x=0} = \mathrm{e}^{\mathrm{i} R \beta }\phi|_{x=R}, \quad \partial_x \phi|_{x=0} = \mathrm{e}^{\mathrm{i} R \beta } \partial_x \phi|_{x=R} }[/math]
and appropriate boundary conditions at the body surfaces, has an eigenvalue in the interval [math]\displaystyle{ \ (k,\pi/R] \ }[/math]. This corresponds to a wave travelling down the array with phase factor
[math]\displaystyle{ \ Q_j = \mathrm{e}^{\mathrm{i} j R \beta}. }[/math]
An example is given in the plot.