Difference between revisions of "Template:Energy contour and preliminaries"
| Line 9: | Line 9: | ||
Applying Green's theorem to <math>\phi</math> and its conjugate <math>\phi^*</math> gives | Applying Green's theorem to <math>\phi</math> and its conjugate <math>\phi^*</math> gives | ||
<center><math> | <center><math> | ||
| − | { \int\int_\mathcal{U}(\phi\nabla^2\phi | + | { \int\int_\mathcal{U}\left(\phi^*\nabla^2\phi - \phi\nabla^2\phi^* \right)dxdz |
| − | = \int_\mathcal{S}(\phi\frac{\partial\phi | + | = \int_\mathcal{S}\left(\phi^*\frac{\partial\phi}{\partial n} - \phi\frac{\partial\phi^*}{\partial n} \right)dl }, |
</math></center> | </math></center> | ||
where <math>n</math> denotes the outward plane normal to the boundary and <math>l</math> denotes the plane parallel to the boundary. | where <math>n</math> denotes the outward plane normal to the boundary and <math>l</math> denotes the plane parallel to the boundary. | ||
As <math>\phi</math> and <math>\phi^*</math> satisfy the Laplace's equation, the left hand side of the Green theorem equation vanishes so that it reduces to | As <math>\phi</math> and <math>\phi^*</math> satisfy the Laplace's equation, the left hand side of the Green theorem equation vanishes so that it reduces to | ||
<center><math> | <center><math> | ||
| − | \Im\int_\mathcal{S}\phi\frac{\partial\phi | + | \Im\int_\mathcal{S}\phi^*\frac{\partial\phi}{\partial n} dl = 0, |
</math></center> | </math></center> | ||
Revision as of 00:34, 28 October 2008
Based on the method used in Evans and Davies 1968, a check can be made to ensure the solutions energy balance. The energy balance equation is derived by applying Green's theorem to [math]\displaystyle{ \phi }[/math] and its conjugate. The domain of integration is shown in the figure on the right.
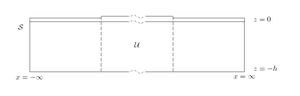
Applying Green's theorem to [math]\displaystyle{ \phi }[/math] and its conjugate [math]\displaystyle{ \phi^* }[/math] gives
where [math]\displaystyle{ n }[/math] denotes the outward plane normal to the boundary and [math]\displaystyle{ l }[/math] denotes the plane parallel to the boundary. As [math]\displaystyle{ \phi }[/math] and [math]\displaystyle{ \phi^* }[/math] satisfy the Laplace's equation, the left hand side of the Green theorem equation vanishes so that it reduces to