Difference between revisions of "Burgers Equation"
| (16 intermediate revisions by 3 users not shown) | |||
| Line 26: | Line 26: | ||
\partial _{t}u+u\partial _{x}u=\nu \partial _{x}^{2}u | \partial _{t}u+u\partial _{x}u=\nu \partial _{x}^{2}u | ||
</math></center> | </math></center> | ||
| − | (changing variables to <math>u | + | (changing variables to <math>u</math> and this equation is known as Burgers equation. |
==Travelling Wave Solution== | ==Travelling Wave Solution== | ||
| Line 36: | Line 36: | ||
This leads to the equations | This leads to the equations | ||
<center><math> | <center><math> | ||
| − | - | + | -cu^{\prime }+u^{\prime }u-\nu u^{\prime \prime }=0 |
</math></center> | </math></center> | ||
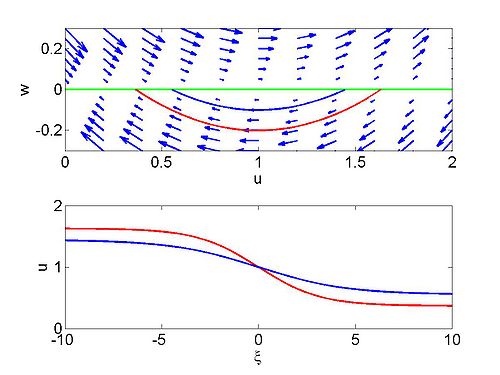
We begin by looking at the phase plane for this system, writing <math>w=u^{\prime | We begin by looking at the phase plane for this system, writing <math>w=u^{\prime | ||
}</math> so that | }</math> so that | ||
<center><math>\begin{matrix} | <center><math>\begin{matrix} | ||
| − | \ | + | \dfrac{\mathrm{d}u}{\mathrm{d}\xi } &=&w \\ |
| − | \ | + | \dfrac{\mathrm{d}w}{\mathrm{d}\xi } &=&\frac{1}{\nu }\left( w\left( u-c\right) \right) |
\end{matrix}</math></center> | \end{matrix}</math></center> | ||
This is a degenerate system with the entire <math>u</math> axis being equilibria. | This is a degenerate system with the entire <math>u</math> axis being equilibria. | ||
| Line 52: | Line 52: | ||
can be integrated to give | can be integrated to give | ||
<center><math> | <center><math> | ||
| − | -cu+\frac{1}{2}\left( u\right) ^{2}-\nu u^{\prime }=c_{1} | + | -cu+\frac{1}{2}\left( u\right) ^{2}-\nu u^{\prime} =c_{1} |
</math></center> | </math></center> | ||
which can be rearranged to give | which can be rearranged to give | ||
<center><math> | <center><math> | ||
| − | u^{\prime }=\frac{1}{2\nu }\left( \left( u\right) ^{2}-2cu | + | u^{\prime }=\frac{1}{2\nu }\left( \left( u\right) ^{2}-2cu-2c_{1}\right) |
| − | |||
</math></center> | </math></center> | ||
We define the two roots of the quadratic <math>\left( u\right) ^{2}-2\nu | We define the two roots of the quadratic <math>\left( u\right) ^{2}-2\nu | ||
| − | u | + | u-2c_{1}=0</math> by <math>u_{1}</math> and <math>u_{2}</math> |
and we assume that <math>u_{2} < u_{1}</math>. Note that there is only a bounded | and we assume that <math>u_{2} < u_{1}</math>. Note that there is only a bounded | ||
solution if we have two real roots and for the bounded solution | solution if we have two real roots and for the bounded solution | ||
| Line 67: | Line 66: | ||
is | is | ||
<center><math> | <center><math> | ||
| − | + | c=\frac{1}{2}\left( u_{1}+u_{2}\right) | |
</math></center> | </math></center> | ||
The equation can therefore be written as | The equation can therefore be written as | ||
| Line 90: | Line 89: | ||
We solve this by solving in Fourier space to give | We solve this by solving in Fourier space to give | ||
<center><math> | <center><math> | ||
| − | \partial _{t}\hat{u}=-\frac{1}{2}ik\left( u^{2}\right) -\nu k^{2}\hat{u} | + | \partial _{t}\hat{u}=-\frac{1}{2}ik \widehat{\left( u^{2}\right)} -\nu k^{2}\hat{u} |
| − | |||
| − | |||
| − | |||
| − | |||
</math></center> | </math></center> | ||
| + | Then we solve each of the steps in turn | ||
for a small time interval to give | for a small time interval to give | ||
<center><math>\begin{matrix} | <center><math>\begin{matrix} | ||
| Line 104: | Line 100: | ||
\exp \left( -\nu k^{2}\Delta t\right) | \exp \left( -\nu k^{2}\Delta t\right) | ||
\end{matrix}</math></center> | \end{matrix}</math></center> | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | ! Phase plane for a travelling wave solution | ||
| + | ! Numerical solution of Burgers equation | ||
| + | |- | ||
| + | | [[Image:Burgers_phase.jpg|thumb|right|500px|Phase plane for a travelling wave solution of Burgers equation]] | ||
| + | | [[Image:File-Burgers2.gif|thumb|right|500px| Numerical solution of Burgers equation]] | ||
| + | |||
| + | |} | ||
==Exact Solution of Burgers equations== | ==Exact Solution of Burgers equations== | ||
| Line 115: | Line 121: | ||
<center><math> | <center><math> | ||
\partial _{t}u+\partial _{x}\left( \frac{u^{2}}{2}-\nu \partial _{x}u\right) | \partial _{t}u+\partial _{x}\left( \frac{u^{2}}{2}-\nu \partial _{x}u\right) | ||
| − | =0 | + | =0 |
</math></center> | </math></center> | ||
We want to find a function <math>\psi \left( x,t\right) </math> such that | We want to find a function <math>\psi \left( x,t\right) </math> such that | ||
<center><math> | <center><math> | ||
\partial _{x}\psi =u,\ \ \partial _{t}\psi =\nu \partial _{x}u-\frac{u^{2}}{2 | \partial _{x}\psi =u,\ \ \partial _{t}\psi =\nu \partial _{x}u-\frac{u^{2}}{2 | ||
| − | } | + | } |
</math></center> | </math></center> | ||
Note that because <math>\partial _{x}\partial _{t}\psi =\partial _{t}\partial | Note that because <math>\partial _{x}\partial _{t}\psi =\partial _{t}\partial | ||
| Line 133: | Line 139: | ||
\psi =-2\nu \log \left( \phi \right) | \psi =-2\nu \log \left( \phi \right) | ||
</math></center> | </math></center> | ||
| − | + | From this we can obtain the three results: | |
| − | |||
| − | |||
| − | |||
| − | |||
<center><math> | <center><math> | ||
| − | \partial _{x}^{2}\psi =2\nu \left( \frac{\partial _{x}\phi }{\phi }\right) | + | \begin{align} |
| − | ^{2}-\frac{2\nu }{\phi }\partial _{x}^{2}\phi | + | \partial _{x}\psi &=-2\nu \frac{\partial _{x}\phi }{\phi } \\ |
| − | + | \partial _{x}^{2}\psi &=2\nu \left( \frac{\partial _{x}\phi }{\phi }\right) | |
| − | + | ^{2}-\frac{2\nu }{\phi }\partial _{x}^{2}\phi \\ | |
| − | + | \partial _{t}\psi &=-2\nu \frac{\partial _{t}\phi }{\phi } | |
| − | \partial _{t}\psi =-2\nu \frac{\partial _{t}\phi }{\phi } | + | \end{align} |
</math></center> | </math></center> | ||
Therefore | Therefore | ||
| Line 154: | Line 156: | ||
<center><math> | <center><math> | ||
-2\nu \frac{\partial _{t}\phi }{\phi }=2\nu ^{2}\left( \frac{\partial | -2\nu \frac{\partial _{t}\phi }{\phi }=2\nu ^{2}\left( \frac{\partial | ||
| − | _{x}\phi }{\phi }\right) ^{2} | + | _{x}\phi }{\phi }\right) ^{2} |
| + | -2\nu^2 \frac{\partial_x^2\phi}{\phi} | ||
| + | -\frac{1}{2}\left( 2\nu \frac{\partial _{x}\phi | ||
}{\phi }\right) ^{2} | }{\phi }\right) ^{2} | ||
</math></center> | </math></center> | ||
| Line 161: | Line 165: | ||
\partial _{t}\phi =\nu \partial _{x}^{2}\phi | \partial _{t}\phi =\nu \partial _{x}^{2}\phi | ||
</math></center> | </math></center> | ||
| − | which is just the | + | which is just the diffusion equation. Note that we also have to transform the |
boundary conditions. We have | boundary conditions. We have | ||
<center><math> | <center><math> | ||
| Line 169: | Line 173: | ||
We can write this as | We can write this as | ||
<center><math> | <center><math> | ||
| − | \frac{d}{ | + | \frac{\mathrm{d}}{\mathrm{d}x}\left( \log \left( \phi \right) \right) =-\frac{1}{2\nu }F\left( |
x\right) | x\right) | ||
</math></center> | </math></center> | ||
| Line 175: | Line 179: | ||
<center><math> | <center><math> | ||
\phi \left( x,0\right) =\Phi \left( x\right) =\exp \left( -\frac{1}{2\nu } | \phi \left( x,0\right) =\Phi \left( x\right) =\exp \left( -\frac{1}{2\nu } | ||
| − | \int_{0}^{x}F\left( | + | \int_{0}^{x}F\left( s\right) \mathrm{d}s\right) |
</math></center> | </math></center> | ||
We need to solve | We need to solve | ||
| Line 196: | Line 200: | ||
e^{-k^{2}\nu t}\right] \\ | e^{-k^{2}\nu t}\right] \\ | ||
&=&\frac{1}{2\sqrt{\pi \nu t}}\int_{-\infty }^{\infty }\Phi \left( y\right) | &=&\frac{1}{2\sqrt{\pi \nu t}}\int_{-\infty }^{\infty }\Phi \left( y\right) | ||
| − | \exp \left[ -\frac{\left( x-y\right) ^{2}}{4\nu t}\right] | + | \exp \left[ -\frac{\left( x-y\right) ^{2}}{4\nu t}\right] \mathrm{d}y |
\end{matrix}</math></center> | \end{matrix}</math></center> | ||
| − | + | Which can be expressed as | |
<center><math> | <center><math> | ||
\phi \left( x,t\right) =\frac{1}{2\sqrt{\pi \nu t}}\int_{-\infty }^{\infty | \phi \left( x,t\right) =\frac{1}{2\sqrt{\pi \nu t}}\int_{-\infty }^{\infty | ||
| − | }\exp \left[ -\frac{f}{2\nu }\right] | + | }\exp \left[ -\frac{f}{2\nu }\right] \mathrm{d}y |
</math></center> | </math></center> | ||
where | where | ||
<center><math> | <center><math> | ||
| − | f\left( x,y,t\right) =\frac{1}{2\nu }\int_{0}^{y}F\left( s\right) | + | f\left( x,y,t\right) =\frac{1}{2\nu }\int_{0}^{y}F\left( s\right) \mathrm{d}s+\frac{ |
| − | \left( x-y\right) ^{2}}{2t} | + | \left( x-y\right) ^{2}}{2t} |
</math></center> | </math></center> | ||
To find <math>u</math> we recall that | To find <math>u</math> we recall that | ||
<center><math>\begin{matrix} | <center><math>\begin{matrix} | ||
| − | u\left( x,t\right) &=&-2\nu \ | + | u\left( x,t\right) &=&-2\nu \dfrac{\partial _{x}\phi \left( x,t\right) }{\phi |
\left( x,t\right) } \\ | \left( x,t\right) } \\ | ||
| − | &=&\ | + | &=&\dfrac{\int_{-\infty }^{\infty }\left( \frac{x-y}{t}\right) \exp \left[ - |
| − | \ | + | \dfrac{f}{2\nu }\right] \mathrm{d}y}{\int_{-\infty }^{\infty }\exp \left[ -\frac{f}{ |
| − | 2\nu }\right] | + | 2\nu }\right] \mathrm{d}y} |
\end{matrix}</math></center> | \end{matrix}</math></center> | ||
| + | |||
| + | == Lecture Videos == | ||
| + | |||
| + | === Part 1 === | ||
| + | |||
| + | {{#ev:youtube|tVXQmxOG_6Y}} | ||
| + | |||
| + | === Part 2 === | ||
| + | |||
| + | {{#ev:youtube|hzgpMM_wWts}} | ||
| + | |||
| + | === Part 3 === | ||
| + | |||
| + | {{#ev:youtube|uH4B1XsGB-0}} | ||
| + | |||
| + | === Part 4 === | ||
| + | |||
| + | {{#ev:youtube|h6aDmCtJygM}} | ||
| + | |||
| + | === Part 5 === | ||
| + | |||
| + | {{#ev:youtube|CsnUKrLjtyQ}} | ||
Latest revision as of 02:14, 24 October 2020
| Nonlinear PDE's Course | |
|---|---|
| Current Topic | Burgers Equation |
| Next Topic | |
| Previous Topic | Reaction-Diffusion Systems |
Introduction
We have already met the conservation law for the traffic equations
and seen how this leads to shocks. We can smooth this equation by adding dispersion to the equation to give us
where [math]\displaystyle{ \nu \gt 0. }[/math]
The simplest equation of this type is to write
(changing variables to [math]\displaystyle{ u }[/math] and this equation is known as Burgers equation.
Travelling Wave Solution
We can find a travelling wave solution by assuming that
This leads to the equations
We begin by looking at the phase plane for this system, writing [math]\displaystyle{ w=u^{\prime } }[/math] so that
This is a degenerate system with the entire [math]\displaystyle{ u }[/math] axis being equilibria.
We can also solve this equation exactly as follows.
can be integrated to give
which can be rearranged to give
We define the two roots of the quadratic [math]\displaystyle{ \left( u\right) ^{2}-2\nu u-2c_{1}=0 }[/math] by [math]\displaystyle{ u_{1} }[/math] and [math]\displaystyle{ u_{2} }[/math] and we assume that [math]\displaystyle{ u_{2} \lt u_{1} }[/math]. Note that there is only a bounded solution if we have two real roots and for the bounded solution [math]\displaystyle{ u_{2} \lt u \lt u_{1} }[/math]. We note that the wave speed is
The equation can therefore be written as
which has solution
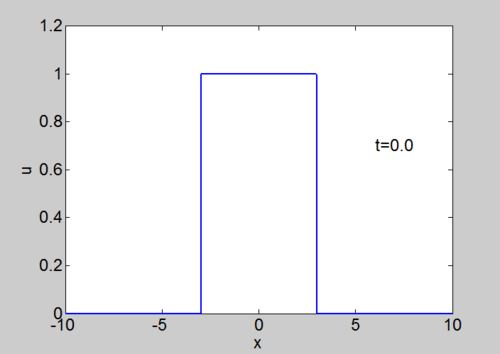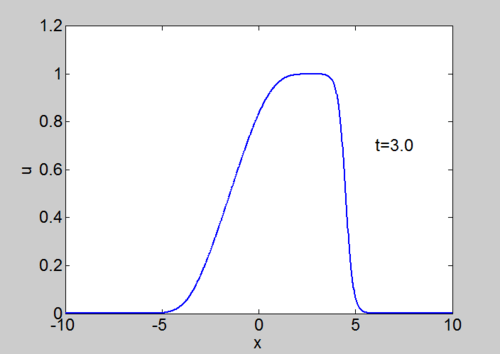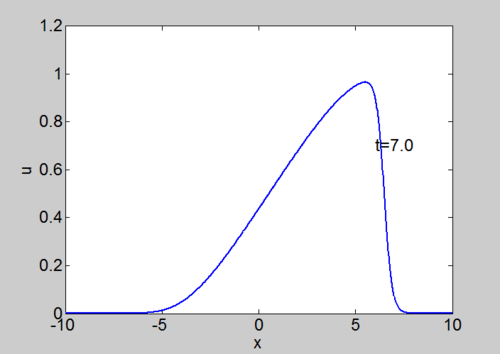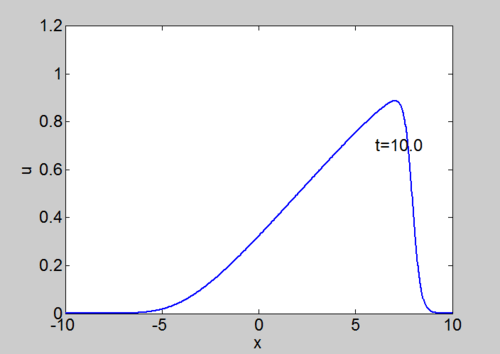
Numerical Solution of Burgers equation
We can solve the equation using our split step spectral method. The equation can be written as
We solve this by solving in Fourier space to give
Then we solve each of the steps in turn for a small time interval to give
| Phase plane for a travelling wave solution | Numerical solution of Burgers equation |
|---|---|
Exact Solution of Burgers equations
We can find an exact solution to Burgers equation. We want to solve
Frist we write the equation as
We want to find a function [math]\displaystyle{ \psi \left( x,t\right) }[/math] such that
Note that because [math]\displaystyle{ \partial _{x}\partial _{t}\psi =\partial _{t}\partial _{x}\psi }[/math] we will satisfy Burgers equation. This gives us the following equation for [math]\displaystyle{ \psi }[/math]
We introduce the Cole-Hopf transformation
From this we can obtain the three results:
Therefore
becomes
or
which is just the diffusion equation. Note that we also have to transform the boundary conditions. We have
We can write this as
which has solution
We need to solve
We take the Fourier transform and obtain
which has solution
We can then use the convolution theorem to write
Which can be expressed as
where
To find [math]\displaystyle{ u }[/math] we recall that