Difference between revisions of "Wavemaker Theory"
| (68 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | = | + | {{Ocean Wave Interaction with Ships and Offshore Structures |
| + | | chapter title = Wavemaker Theory | ||
| + | | next chapter = [[Ship Kelvin Wake]] | ||
| + | | previous chapter = [[Wave Momentum Flux]] | ||
| + | }} | ||
| − | + | {{complete pages}} | |
| − | + | == Introduction == | |
| − | |||
| − | + | [[Image:Wave_maker.png|600px|right|thumb|Wavemaker]] | |
| − | + | We will derive the potential in a two-dimensional wavetank due the motion of the wavemaker. The method is based on the [[:Category:Eigenfunction Matching Method|Eigenfunction Matching Method]]. | |
| + | A paddle is undergoing small amplitude horizontal oscillations with displacement | ||
| + | <center><math> \zeta (z,t) = \mathrm{Re} \left \{\frac{1}{-\mathrm{i}\omega} f(z) e^{-i\omega t} \right \} </math></center> | ||
| + | where <math> f(z) \, </math> is assumed known. Since the time <math>t=0 \,</math> is arbitrary we can assume that | ||
| + | <math>f(z)\,</math> is real but this is not necessary. | ||
| + | Because the oscillations are small the [[Linear and Second-Order Wave Theory| linear equations]] apply (which will be given formally below). | ||
| + | This excitation creates plane progressive waves with amplitude <math> A \, </math> down the tank. The principal objective of wavemaker theory is to determine <math> A \, </math> | ||
| + | as a function of <math> \omega, f(z) \, </math> and <math> h \, </math>. Time-dependent wavemaker theories can also be developed. | ||
| − | + | == Expansion of the solution == | |
| − | + | {{frequency definition}} | |
| − | |||
| − | + | {{velocity potential in frequency domain}} | |
| − | + | The equations therefore become | |
| + | {{standard linear wave scattering equations without body condition}} | ||
| + | The boundary condition at the wavemaker is | ||
| + | <center> | ||
| + | <math> | ||
| + | \left. \partial_x\phi \right|_{x=0} = \partial_t \xi = f(z). | ||
| + | </math> | ||
| + | </center> | ||
| + | We must also apply the [[Sommerfeld Radiation Condition]] | ||
| + | as <math>x\rightarrow\infty</math>. This essentially implies | ||
| + | that the only wave at infinity is propagating away. | ||
| − | + | {{separation of variables for a free surface}} | |
| − | + | == Expansion in Eigenfunctions == | |
| − | + | The wavemaker velocity potential <math> \phi \,</math> can be expressed simply in terms of eigenfunctions | |
| − | + | <center><math> \phi = \sum_{n=0}^{\infty} a_n \phi_n (z) e^{-k_n x} </math></center> | |
| − | + | and we can solve for the coefficients by matching at <math>x=0 \,</math> | |
| − | + | <center><math> \left. \phi_x \right|_{x=0} = \sum_{n=0}^{\infty} -k_n a_n \phi_n (z) = f(z) | |
| − | |||
| − | <center><math> \ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
</math></center> | </math></center> | ||
| − | + | It follows that | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | It follows that | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | <center><math> | + | <center><math> a_n = -\frac{1}{k_n A_n} \int_{-h}^0 \phi_n(z) f(z)\mathrm{d}z </math></center> |
| − | |||
| − | |||
| + | === Far Field Wave === | ||
| + | One of the primary objecives of wavemaker theory is to determine the far-field wave amplitude <math> A \, </math> in terms of <math> f(z) \, </math>. | ||
The far-field wave component representing progagating waves is given by: | The far-field wave component representing progagating waves is given by: | ||
| − | <center><math> \ | + | <center><math> \lim_{x\to\infty} \phi = a_0 \phi_0(z) e^{-k_0 x} = |
| + | a_0 \frac{\cos k_0(z+h)}{\cos k_0 h } e^{-k_0 x} </math></center> | ||
| − | < | + | Note that <math> k_0 \, </math> is imaginery. We therefore obtain the complex amplitude of the propagating wave at infinity, namely modulus and phase, in terms of the wave maker displacement <math> f(z) \, </math>. |
| − | + | For what type of <math> f(z) \, </math> are the non-wavelike modes zero? It is easy to verify by virtue of orthogonality that | |
| − | < | + | <center><math> f(z) \ \sim \ \phi_0 (z) </math></center> |
| − | + | Unfortunately this is not a "practical" displacement since <math> \phi_0 (z) \, </math> depends on <math> \omega\, </math>, so one would need to build a flexible paddle. | |
| − | + | == Matlab Code == | |
| − | + | A program to calculate the coefficients for the wave maker problems can be found here | |
| + | [http://www.math.auckland.ac.nz/~meylan/code/eigenfunction_matching/wavemaker.m wavemaker.m] | ||
| − | + | === Additional code === | |
| − | + | This program requires | |
| − | + | [http://www.math.auckland.ac.nz/~meylan/code/dispersion/dispersion_free_surface.m dispersion_free_surface.m] | |
| − | + | to run | |
| − | |||
| − | |||
----- | ----- | ||
| − | This article is based on the MIT open course notes and the original article can be found | + | This article is based in part on the MIT open course notes and the original article can be found |
[http://ocw.mit.edu/NR/rdonlyres/Mechanical-Engineering/2-24Spring-2002/737E217E-0582-45D5-B1F9-B2ECF977C66E/0/lecture6.pdf here] | [http://ocw.mit.edu/NR/rdonlyres/Mechanical-Engineering/2-24Spring-2002/737E217E-0582-45D5-B1F9-B2ECF977C66E/0/lecture6.pdf here] | ||
| + | |||
| + | [[Ocean Wave Interaction with Ships and Offshore Energy Systems]] | ||
[[Category:Eigenfunction Matching Method]] | [[Category:Eigenfunction Matching Method]] | ||
| − | + | [[Category:Pages with Matlab Code]] | |
| − | [[ | + | [[Category:Complete Pages]] |
Latest revision as of 01:13, 5 May 2023
| Wave and Wave Body Interactions | |
|---|---|
| Current Chapter | Wavemaker Theory |
| Next Chapter | Ship Kelvin Wake |
| Previous Chapter | Wave Momentum Flux |
Introduction
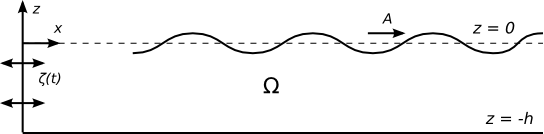
We will derive the potential in a two-dimensional wavetank due the motion of the wavemaker. The method is based on the Eigenfunction Matching Method. A paddle is undergoing small amplitude horizontal oscillations with displacement
where [math]\displaystyle{ f(z) \, }[/math] is assumed known. Since the time [math]\displaystyle{ t=0 \, }[/math] is arbitrary we can assume that [math]\displaystyle{ f(z)\, }[/math] is real but this is not necessary. Because the oscillations are small the linear equations apply (which will be given formally below). This excitation creates plane progressive waves with amplitude [math]\displaystyle{ A \, }[/math] down the tank. The principal objective of wavemaker theory is to determine [math]\displaystyle{ A \, }[/math] as a function of [math]\displaystyle{ \omega, f(z) \, }[/math] and [math]\displaystyle{ h \, }[/math]. Time-dependent wavemaker theories can also be developed.
Expansion of the solution
We also assume that Frequency Domain Problem with frequency [math]\displaystyle{ \omega }[/math] and we assume that all variables are proportional to [math]\displaystyle{ \exp(-\mathrm{i}\omega t)\, }[/math]
The water motion is represented by a velocity potential which is
denoted by [math]\displaystyle{ \phi\, }[/math] so that
[math]\displaystyle{ \Phi(\mathbf{x},t) = \mathrm{Re} \left\{\phi(\mathbf{x},\omega)e^{-\mathrm{i} \omega t}\right\}. }[/math]
The equations therefore become
(note that the last expression can be obtained from combining the expressions:
where [math]\displaystyle{ \alpha = \omega^2/g \, }[/math]) The boundary condition at the wavemaker is
[math]\displaystyle{ \left. \partial_x\phi \right|_{x=0} = \partial_t \xi = f(z). }[/math]
We must also apply the Sommerfeld Radiation Condition as [math]\displaystyle{ x\rightarrow\infty }[/math]. This essentially implies that the only wave at infinity is propagating away.
Separation of variables for a free surface
We use separation of variables
We express the potential as
[math]\displaystyle{ \phi(x,z) = X(x)Z(z)\, }[/math]
and then Laplace's equation becomes
[math]\displaystyle{ \frac{X^{\prime\prime}}{X} = - \frac{Z^{\prime\prime}}{Z} = k^2 }[/math]
The separation of variables equation for deriving free surface eigenfunctions is as follows:
[math]\displaystyle{ Z^{\prime\prime} + k^2 Z =0. }[/math]
subject to the boundary conditions
[math]\displaystyle{ Z^{\prime}(-h) = 0 }[/math]
and
[math]\displaystyle{ Z^{\prime}(0) = \alpha Z(0) }[/math]
We can then use the boundary condition at [math]\displaystyle{ z=-h \, }[/math] to write
[math]\displaystyle{ Z = \frac{\cos k(z+h)}{\cos kh} }[/math]
where we have chosen the value of the coefficent so we have unit value at [math]\displaystyle{ z=0 }[/math]. The boundary condition at the free surface ([math]\displaystyle{ z=0 \, }[/math]) gives rise to:
which is the Dispersion Relation for a Free Surface
The above equation is a transcendental equation. If we solve for all roots in the complex plane we find that the first root is a pair of imaginary roots. We denote the imaginary solutions of this equation by [math]\displaystyle{ k_{0}=\pm ik \, }[/math] and the positive real solutions by [math]\displaystyle{ k_{m} \, }[/math], [math]\displaystyle{ m\geq1 }[/math]. The [math]\displaystyle{ k \, }[/math] of the imaginary solution is the wavenumber. We put the imaginary roots back into the equation above and use the hyperbolic relations
[math]\displaystyle{ \cos ix = \cosh x, \quad \sin ix = i\sinh x, }[/math]
to arrive at the dispersion relation
[math]\displaystyle{ \alpha = k\tanh kh. }[/math]
We note that for a specified frequency [math]\displaystyle{ \omega \, }[/math] the equation determines the wavenumber [math]\displaystyle{ k \, }[/math].
Finally we define the function [math]\displaystyle{ Z(z) \, }[/math] as
[math]\displaystyle{ \chi_{m}\left( z\right) =\frac{\cos k_{m}(z+h)}{\cos k_{m}h},\quad m\geq0 }[/math]
as the vertical eigenfunction of the potential in the open water region. From Sturm-Liouville theory the vertical eigenfunctions are orthogonal. They can be normalised to be orthonormal, but this has no advantages for a numerical implementation. It can be shown that
[math]\displaystyle{ \int\nolimits_{-h}^{0}\chi_{m}(z)\chi_{n}(z) \mathrm{d} z=A_{n}\delta_{mn} }[/math]
where
[math]\displaystyle{ A_{n}=\frac{1}{2}\left( \frac{\cos k_{n}h\sin k_{n}h+k_{n}h}{k_{n}\cos ^{2}k_{n}h}\right). }[/math]
Expansion in Eigenfunctions
The wavemaker velocity potential [math]\displaystyle{ \phi \, }[/math] can be expressed simply in terms of eigenfunctions
and we can solve for the coefficients by matching at [math]\displaystyle{ x=0 \, }[/math]
It follows that
Far Field Wave
One of the primary objecives of wavemaker theory is to determine the far-field wave amplitude [math]\displaystyle{ A \, }[/math] in terms of [math]\displaystyle{ f(z) \, }[/math]. The far-field wave component representing progagating waves is given by:
Note that [math]\displaystyle{ k_0 \, }[/math] is imaginery. We therefore obtain the complex amplitude of the propagating wave at infinity, namely modulus and phase, in terms of the wave maker displacement [math]\displaystyle{ f(z) \, }[/math].
For what type of [math]\displaystyle{ f(z) \, }[/math] are the non-wavelike modes zero? It is easy to verify by virtue of orthogonality that
Unfortunately this is not a "practical" displacement since [math]\displaystyle{ \phi_0 (z) \, }[/math] depends on [math]\displaystyle{ \omega\, }[/math], so one would need to build a flexible paddle.
Matlab Code
A program to calculate the coefficients for the wave maker problems can be found here wavemaker.m
Additional code
This program requires dispersion_free_surface.m to run
This article is based in part on the MIT open course notes and the original article can be found here
Ocean Wave Interaction with Ships and Offshore Energy Systems