Waves reflecting off a vertical wall

Breakwater

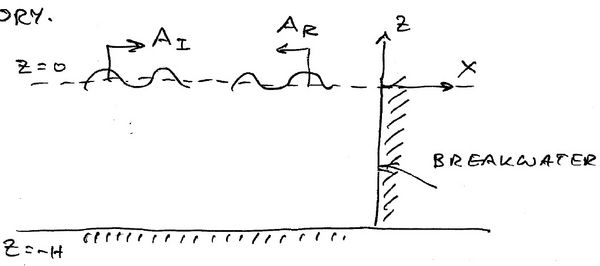
Waves reflecting off a vertical wall is one of the few very important analytical solutions of regular waves interacting with solid boundaries seen in practice. The other is wavemaker theory. Let the incident wave elevation be

[math]\displaystyle{ \zeta_I = \mathrm{Re} \left \{ A_I e^{-\mathrm{i} k x+\mathrm{i}\omega t} \right \} }[/math]

and the reflected is

[math]\displaystyle{ \zeta_R = \mathrm{Re} \left \{ A_R e^{\mathrm{i}k x+\mathrm{i}\omega t} \right \} }[/math]

where the sign of the [math]\displaystyle{ e^{\mathrm{i} k x}\, }[/math] term has been reversed to denote a wave propagating to the left. [math]\displaystyle{ A_R\, }[/math] can be complex in order to allow for phase differences.

The corresponding velocity potentials are

[math]\displaystyle{ \Phi_I = \mathrm{Re} \left \{ \frac{\mathrm{i} gA_I}{\omega} \frac{\cosh k k h (z+h)}{\cosh k h} e^{-\mathrm{i} k x + \mathrm{i}\omega t} \right \} }[/math] [math]\displaystyle{ \Phi_R = \mathrm{Re} \left \{ \frac{\mathrm{i} gA_R}{\omega} \frac{\cosh k (z+h)}{\cosh k h} e^{\mathrm{i} k x +\mathrm{i}\omega t} \right \} }[/math]

On [math]\displaystyle{ x = 0 \, }[/math]:

[math]\displaystyle{ \frac{\partial}{\partial x} \left( \Phi_I + \Phi_R \right) = 0 }[/math]

or

[math]\displaystyle{ - \mathrm{i} k A_I + \mathrm{i} k A_R \Longrightarrow A_R = A_I \equiv A }[/math]

The resulting total velocity potential is

[math]\displaystyle{ \Phi = \Phi_I + \Phi_R = \mathrm{Re} \left \{ \frac{\mathrm{i}gA_R}{\omega} \frac{\cosh k (z+h}{\cosh kh} e^{\mathrm{i}\omega t} \left( e^{\mathrm{i}kx} + e^{-\mathrm{i}kx} \right) \right \} }[/math] [math]\displaystyle{ = 2 A \mathrm{Re} \left \{ \frac{\mathrm{i}g}{\omega} \frac{\cosh k (z+h)}{\cosh kh} \cos kx e^{\mathrm{i}\omega t} \right \} }[/math]

The resulting standing-wave elevation is:

[math]\displaystyle{ \zeta = \zeta_I + \zeta_R = 2 A \cos k x \cos \omega t \, }[/math]