Difference between revisions of "Waves reflecting off a vertical wall"
| Line 1: | Line 1: | ||
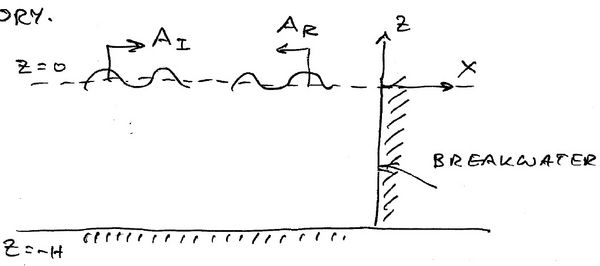
[[Image:Breakwater.jpg|thumb|right|600px|Breakwater]] | [[Image:Breakwater.jpg|thumb|right|600px|Breakwater]] | ||
Waves reflecting off a vertical wall is one of the few very important analytical solutions of regular waves interacting with solid boundaries seen in practice. The other is wavemaker theory. | Waves reflecting off a vertical wall is one of the few very important analytical solutions of regular waves interacting with solid boundaries seen in practice. The other is wavemaker theory. | ||
| − | + | ||
| − | + | {{incident plane wave}} | |
| − | + | ||
| − | + | The refl | |
| − | |||
The corresponding velocity potentials are | The corresponding velocity potentials are | ||
Revision as of 21:45, 3 April 2010
Waves reflecting off a vertical wall is one of the few very important analytical solutions of regular waves interacting with solid boundaries seen in practice. The other is wavemaker theory.
The equation is subject to some radiation conditions at infinity. We assume the following. [math]\displaystyle{ \phi^{\mathrm{I}}\, }[/math] is a plane wave travelling in the [math]\displaystyle{ x }[/math] direction,
where [math]\displaystyle{ A }[/math] is the wave amplitude (in potential) [math]\displaystyle{ \mathrm{i} k }[/math] is the positive imaginary solution of the Dispersion Relation for a Free Surface (note we are assuming that the time dependence is of the form [math]\displaystyle{ \exp(-\mathrm{i}\omega t) }[/math]) and
The refl
The corresponding velocity potentials are
On [math]\displaystyle{ x = 0 \, }[/math]:
or
The resulting total velocity potential is
The resulting standing-wave elevation is: