Difference between revisions of "Example Calculations for the KdV and IST"
| Line 68: | Line 68: | ||
where <math>\nu</math> is an appropriate constant to make the function increase in value | where <math>\nu</math> is an appropriate constant to make the function increase in value | ||
sufficiently rapidly but not too rapidly. | sufficiently rapidly but not too rapidly. | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | ! Animation | ||
| + | ! Three-dimensional plot. | ||
| + | |- | ||
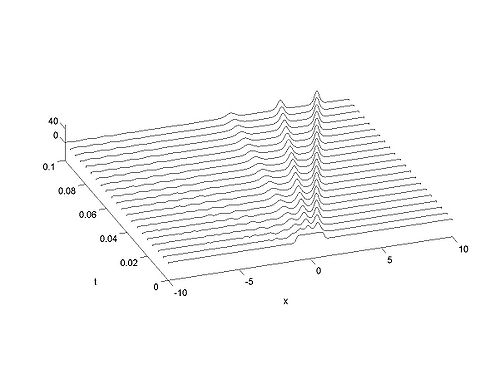
| + | | [[Image:Wide_function.gif|thumb|right|500px|Evolution of <math>u(x,t)</math>.]] | ||
| + | | [[Image:Widefunction.jpg|thumb|right|500px|Evolution of <math>u(x,t)</math> ]] | ||
| + | |||
| + | |} | ||
Revision as of 10:57, 23 September 2010
| Nonlinear PDE's Course | |
|---|---|
| Current Topic | Example Calculations for the KdV and IST |
| Next Topic | Connection betwen KdV and the Schrodinger Equation |
| Previous Topic | Reaction-Diffusion Systems |
Example1 Delta function potential.
We have already calculated the scattering data for the delta function potential. The scattering data is
The spectral data evolves as
so that
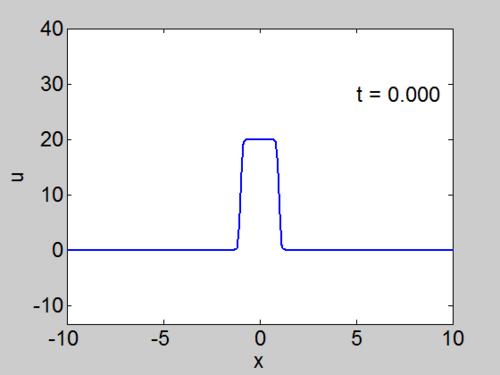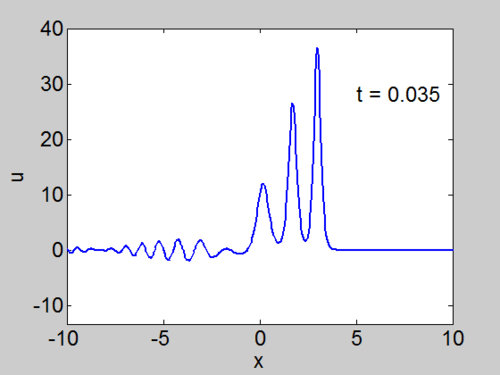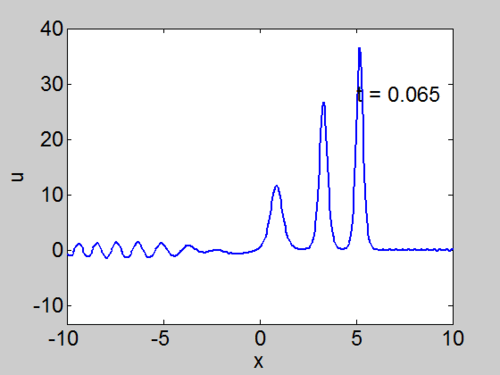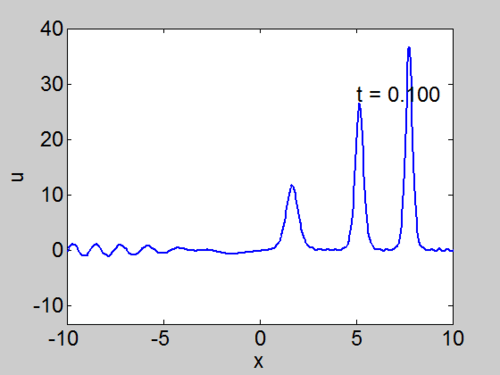
Example 2 A Hat Function
We solve for the case when
For this case we need to solve
which has solution and
which has solution.
Recall that the solitons have amplitude [math]\displaystyle{ 2k_{n}^{2} }[/math] or [math]\displaystyle{ -2\lambda_{n} }[/math]. This can be seen in the height of the solitary waves.
We cannot work with a hat function numerically, because the jump in [math]\displaystyle{ u }[/math] leads to high frequencies which dominate the response.. We can smooth our function by a number of methods. We use here the function [math]\displaystyle{ \tanh\left( x\right) }[/math] so we write
where [math]\displaystyle{ \nu }[/math] is an appropriate constant to make the function increase in value sufficiently rapidly but not too rapidly.
| Animation | Three-dimensional plot. |
|---|---|