Difference between revisions of "Wavemaker Theory"
| Line 5: | Line 5: | ||
We will derive the potential in a two-dimensional wavetank due the motion of the wavemaker. The method is based on the [[:Category:Eigenfunction Matching Method|Eigenfunction Matching Method]]. | We will derive the potential in a two-dimensional wavetank due the motion of the wavemaker. The method is based on the [[:Category:Eigenfunction Matching Method|Eigenfunction Matching Method]]. | ||
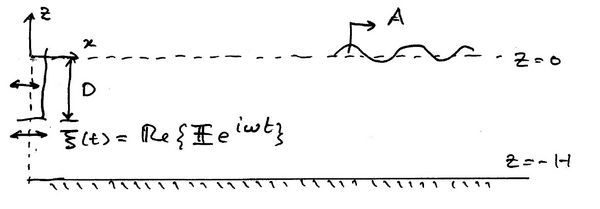
A paddle with draft <math> D\, </math> is undergoing small amplitude horizontal oscillations with displacement | A paddle with draft <math> D\, </math> is undergoing small amplitude horizontal oscillations with displacement | ||
| − | <center><math> \xi (t) = \mathfrak{Re} \left \{ | + | <center><math> \xi (t) = \mathfrak{Re} \left \{ f(z) e^{i\omega t} \right \} </math></center> |
| − | where <math> | + | where <math> f(z) </math> is assumed known. Since the time <math>t=0</math> is arbitrary we can assume that |
| + | <math>f(z)</math> is real but this is not necessary. | ||
Because the oscillations are small the [[Linear and Second-Order Wave Theory| linear equations]] apply (which will be given formally below). | Because the oscillations are small the [[Linear and Second-Order Wave Theory| linear equations]] apply (which will be given formally below). | ||
| − | This excitation creates plane progressive waves with amplitude <math> A \, </math> down the tank. The principal objective of wavemaker theory is to determine <math> A \, </math> as a function of <math> \omega, | + | This excitation creates plane progressive waves with amplitude <math> A \, </math> down the tank. The principal objective of wavemaker theory is to determine <math> A \, </math> |
| + | as a function of <math> \omega, f(z) \, </math> and <math> H \, </math>. Time-dependent wavemaker theories can also be developed. | ||
= Expansion of the solution = | = Expansion of the solution = | ||
Revision as of 01:14, 29 February 2008
Introduction
We will derive the potential in a two-dimensional wavetank due the motion of the wavemaker. The method is based on the Eigenfunction Matching Method. A paddle with draft [math]\displaystyle{ D\, }[/math] is undergoing small amplitude horizontal oscillations with displacement
where [math]\displaystyle{ f(z) }[/math] is assumed known. Since the time [math]\displaystyle{ t=0 }[/math] is arbitrary we can assume that [math]\displaystyle{ f(z) }[/math] is real but this is not necessary. Because the oscillations are small the linear equations apply (which will be given formally below). This excitation creates plane progressive waves with amplitude [math]\displaystyle{ A \, }[/math] down the tank. The principal objective of wavemaker theory is to determine [math]\displaystyle{ A \, }[/math] as a function of [math]\displaystyle{ \omega, f(z) \, }[/math] and [math]\displaystyle{ H \, }[/math]. Time-dependent wavemaker theories can also be developed.
Expansion of the solution
In general, the wavemaker displacement at [math]\displaystyle{ X=0\, }[/math] may be written in the form
where [math]\displaystyle{ \Pi(Z) \, }[/math] is a known function of [math]\displaystyle{ Z \, }[/math]. The standard linear equations apply. Let the total velocity potential be
where
The first term is a velocity potential that represents a Linear Plane Progressive Regular Wave down the tank with amplitude [math]\displaystyle{ A \, }[/math], yet unknown. Thus
with [math]\displaystyle{ \omega^2 = gK \tanh KH. \, }[/math] (the Dispersion Relation for a Free Surface).
Evanescent modes and separation of variables
The second component potential [math]\displaystyle{ \psi\, }[/math] is by definition a decaying disturbance as [math]\displaystyle{ X \to \infty \, }[/math] and otherwise satisfies the following boundary value problem
The condition on the wavemaker [math]\displaystyle{ (X=0) \, }[/math] is yet to be enforced. Note that unlike [math]\displaystyle{ \phi_\omega,\, \psi \, }[/math] does not representing a propagating wave down the tank so it is called a non-wavelike (evanescent) mode. Such modes do exist as will be shown below. On the wavemaker [math]\displaystyle{ (X=0) \, }[/math] the horizontal velocity due to [math]\displaystyle{ \phi_\omega\, }[/math] and that due to [math]\displaystyle{ \psi\, }[/math] must sum to the forcing velocity due to [math]\displaystyle{ \xi(t) \, }[/math].
When we solve Laplace's equation by separation of variables and apply the bottom boundary conditions we obtain solutions of the form [math]\displaystyle{ e^{-iKX} \cosh K(Z+H) }[/math] (which represent propagating waves and of the form [math]\displaystyle{ \cos \lambda (Z+H) \, }[/math]. Not that this solution satisfies the condition of vanishing value as [math]\displaystyle{ X \to \infty }[/math] provided that [math]\displaystyle{ \lambda \gt 0 \, }[/math]. These solutions satisfy Laplace's equation [math]\displaystyle{ \psi_{XX} + \psi_{ZZ} = 0, \, }[/math] for all [math]\displaystyle{ \lambda }[/math] and the seafloor condition : [math]\displaystyle{ \psi_Z = 0, Z=-H. }[/math] The free-surface condition implies that
So for the non-wavelike modes [math]\displaystyle{ \psi, \lambda \, }[/math] must satisfy the Dispersion Relation for a Free Surface,
For positive values of [math]\displaystyle{ \lambda \, }[/math] so that [math]\displaystyle{ e^{-\lambda X} \to 0, X \to + \infty \, }[/math]. Values of [math]\displaystyle{ \lambda_i \, }[/math] satisfying the dispersion relation follow from the solution of the non-dimensional nolinear equation
Solutions [math]\displaystyle{ \omega_i, i = 1, 2, \cdots \, }[/math] exist as shown above with [math]\displaystyle{ \omega_i \sim i \pi \, }[/math] for large [math]\displaystyle{ i \, }[/math]. These values are known as the eigenvalues or eigen-wavenumbers of the non-wavelike modes. The eigen-wavenumber of the wavelike solution [math]\displaystyle{ K\, }[/math] is given by the dispersion relation:
It can easily be shown that setting [math]\displaystyle{ K = i \lambda \, }[/math], the dispersion relation of the non-wavelike nodes follows. In summary the purely imaginary roots of the surface wave dispersion relation and its single real positive root enter the solution of the wavemaker problem.
Orthogonal eigenfunctions
The solution of the for Dispersion Relation for a Free Surface leads to an infinite series of vertical eigenfunctions from Sturm-Liouville theory. This theory also shows that the eigenfunctions are orthogonal and we may define the following orthogonal eigenfunctions in the vertical direction [math]\displaystyle{ Z \, }[/math]:
Selected to satisfy:
So the wavemaker velocity potentials [math]\displaystyle{ \phi_w \, }[/math] and [math]\displaystyle{ \psi\, }[/math] can be expressed simply in terms of their respective eigen modes:
and:
On [math]\displaystyle{ X=0 \, }[/math]:
and
Or:
It follows that:
Far Field Wave
One of the primary objecives of wavemaker theory is to determine [math]\displaystyle{ a_0 \, }[/math] (or the far-field wave amplitude [math]\displaystyle{ A \, }[/math] ) in terms of [math]\displaystyle{ \Pi (Z) \, }[/math]. Multiplying both sides by [math]\displaystyle{ f_0 (Z) \, }[/math], integrating from [math]\displaystyle{ - H \to 0 \, }[/math] and using orthogonality we obtain:
The far-field wave component representing progagating waves is given by:
Plugging in [math]\displaystyle{ a_0\, }[/math] and solving for [math]\displaystyle{ A \, }[/math] we obtain the complex amplitude of the propagating wave at infinity, namely modulus and phase, in terms of the wave maker displacement [math]\displaystyle{ \Pi (Z) \, }[/math] and the other flow parameters.
For what type of [math]\displaystyle{ \Pi(Z) \, }[/math] are the non-wavelike modes [math]\displaystyle{ \psi \equiv 0 \, }[/math]? It is easy to verify by virtue of orthogonality that:
Unfortunately this is not a "practical" displacement since [math]\displaystyle{ f_0 (Z,K) \, }[/math] depends on [math]\displaystyle{ K\, }[/math], thus on [math]\displaystyle{ \omega\, }[/math]. So one would need to build a flexible paddle!
This article is based on the MIT open course notes and the original article can be found here
Ocean Wave Interaction with Ships and Offshore Energy Systems