Nonlinear Shallow Water Waves

Nonlinear PDE's Course
Current Topic	Nonlinear Shallow Water Waves
Next Topic	Reaction-Diffusion Systems
Previous Topic	Traffic Waves

This is a complete page

Introduction

We assume that water is incompressible, viscous effects are negligible and that the typical wave lengths are much larger than the water depth. This allows us to assume Shallow Depth. We assume that the problem has not variation in either the $y$ or $z$ direction. The fluid is governed by two parameters, $u$, the velocity of the water, and $h$ the water depth (not that this is not the still water depth since the problem is nonlinear).

The theory we present here is discussed in Stoker 1957, Billingham and King 2000 and Johnson 1997.

Equations of Motion

The equation for the conservation of mass can derived by considering a a region $[x,x+\mathrm{\Delta }x]$ Conservation of mass then implies that

${\partial }_t{\int }_x^{x+\mathrm{\Delta }x}\rho h(s,t)ds=\rho h(x,t)u(x,t)-\rho h(x+\mathrm{\Delta }x,t)u(x+\mathrm{\Delta }x,t)$

If we take the limit as $\mathrm{\Delta }x\to 0$ we obtain

${\partial }_{t}h(x,t)+{\partial }_x(h(x,t)u(x,t))=0$

A second equation comes from conservation of momentum. In integral form this is

${\partial }_t{\int }_x^{x+\mathrm{\Delta }x}\rho hudx={\rho u^{2}h|}_x^{x+\mathrm{\Delta }x}+{\int }_0^{h(x)}P(x,z,t)dz-{\int }_0^{h(x+\mathrm{\Delta }x)}P(x+\mathrm{\Delta }x,z,t)dz$

where $\rho$ denotes density, and the pressure $P$ is given by

$P=\rho g(h-z)$

(i.e. we have hydrostatic equilibrium). This then gives us

${\partial }_t{\int }_x^{x+\mathrm{\Delta }x}\rho hudx={\rho u^{2}h|}_x^{x+\mathrm{\Delta }x}+\frac{1}{2}\rho g{h(x)}^2-\frac{1}{2}\rho g{h(x+\mathrm{\Delta }x)}^2$

If we then take the limit as $\mathrm{\Delta }x\to 0$ we obtain

${\partial }_t\left(hu\right)={\partial }_x(u^{2}h-\frac{1}{2}g{h}^2)$

We can simplify this using the equation derived from conservation of mass to to obtain

${\partial }_{t}u+u{\partial }_{x}u+g{\partial }_{x}h=0$

The equations

${\partial }_{t}h+u{\partial }_{x}h+h{\partial }_{x}u=0$

and

${\partial }_{t}u+u{\partial }_{x}u+g{\partial }_{x}h=0$

are called the nonlinear shallow water equations. They determine the horizontal water velocity and the local water depth.

We can rewrite them in terms of the local wave speed $c(x,t)=\sqrt{gh(x,t)}$ as follows:

$2{\partial }_{t}c+2u{\partial }_{x}c+c{\partial }_{x}u=0$

${\partial }_{t}u+u{\partial }_{x}u+2c{\partial }_{x}c=0$

These equation are almost identical to those of compressible gas dynamics. Much of our understanding of the equations for water have been found by researchers studying compressible gas dynamics.

Linearized Equations

We can linearize these equations by assuming that $u$ is small and that $h=h_0+\zeta$ where $h_0$ is the average water depth and $\zeta$ is also assumed small. This gives us

${\partial }_t\zeta +h_0{\partial }_{x}u=0$

and

${\partial }_{t}u+g{\partial }_x\zeta =0$

These linear shallow water equations which can be derived from the linear equations for water of finite depth and taking the limit of small depth (see Shallow Depth).

Characteristics

The equations possess characteristics. Adding and subtracting the two equations above we obtain

$\frac{\partial (u\pm 2c)}{\partial t}+(u\pm c)\frac{\partial (u\pm 2c)}{\partial x}=0$

This means that on the $C_{+}$ characteristic, given by

$\frac{d{X}_{+}}{dt}=u+c=u+\sqrt{gh}$

the $C_{+}$ invariant

$R_{+}=u+2c=u+2\sqrt{gh}$

is a constant, and on the $C_{-}$ characteristic, given by

$\frac{d{X}_{-}}{dt}=u-c=u-\sqrt{gh}$

the $C_{-}$ invariant

$R_{-}=u-2c=u-2\sqrt{gh}$

is a constant.

The functions $R_{\pm }(u,c)=u\pm 2c$, are called the Riemannian invariants.

Simple Waves

The problem as formulated can be solved by advancing the solution along the characteristics, but this will in general be quite difficult analytically. However, there is a special class of problems, called Simple Waves in which the solution only changes on one characteristic. They are best illustrated through some examples. Note that the characteristic can meet forming a shock, which is called a bore or a hydraulic jump when it occurs on the surface of the water.

Evolution of the fluid surface $h(x,t)$ for the Dam Break problem

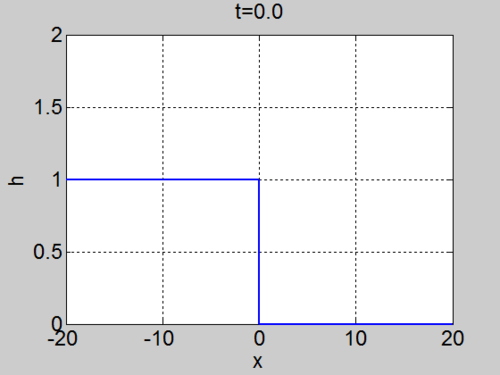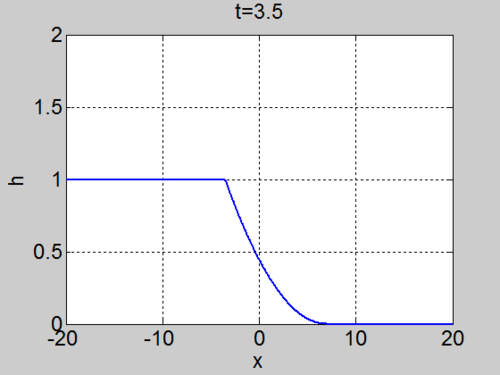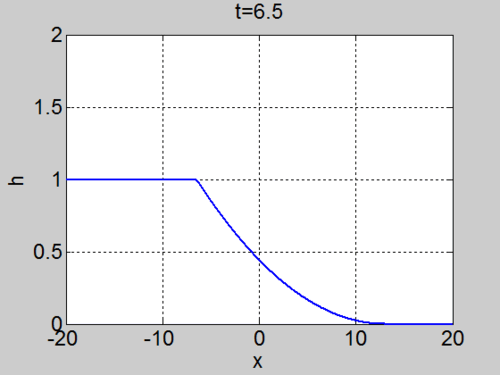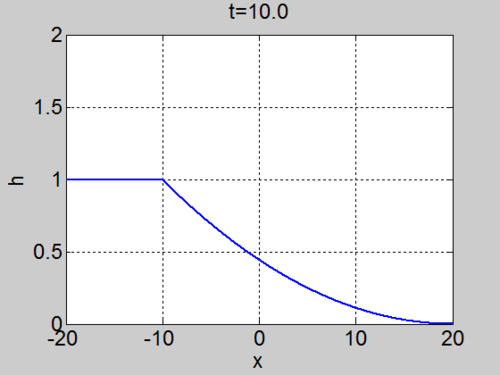
The dam break problem

Assume the water occupies the region $x<0;0<z<h_0$ initially held back by a dam at $x=0$. At $t=0$, the dam is removed (breaks). What is the height of the water $h(x,t)$ for $t>0?$ The initial condition is therefore

$h(x,0)=\{\begin{array}{ll}{h}_0,& x<0\\ 0,& x>0\end{array}$

$u(x,0)=0.$

On the characteristic that originates at $t=0$ for $x<0$,

$R_{\pm }=u\pm 2\sqrt{gh}=\pm 2\sqrt{g{h}_0}=\pm 2c_0$

where $c_0=\sqrt{g{h}_0}$ is the initial (linear) wave speed.

Therefore, if a $C_{+}$ and a $C_{-}$ characteristic from this region intersect, then

$u+2\sqrt{gh}=2c_0,\mathrm{and}u-2\sqrt{gh}=-2c_0$

and hence, $u=0$ and $h=h_0$. Moreover,

$\frac{d{X}_{\pm }}{dt}=u\pm \sqrt{gh}=\pm c_0$

so these characteristics are straight lines in the region $\{x<-c_{0}t\}$ (the undisturbed region).

The $C_{+}$ characteristic leave the region a$\{x<-c_{0}t\}$ and enter $\{x>-c_{0}t\}$. For now we will assume that these characteristics fill the domain (and show that this is true shortly). For $\{x>-c_{0}t\}$, the $C_{-}$ characteristics are given by

$\frac{d{X}_{-}}{dt}=u-\sqrt{gh}$

and on each of the $C_{-}$ characteristics $R_{-}=u-2\sqrt{gh}$ is constant. However, since this region is filled with $C_{+}$ characteristics where $R_{+}=u+2\sqrt{gh}=2c_0$, $u$ and $h$ must be constant on each $C_{-}$ characteristic. This also means that the $C_{-}$ characteristics must be straight lines.

Since the fluid occupies $\{x<0\}$ at $t=0$, these $C_{-}$ characteristics must start at the origin, with

$X_{-}(t)=(u-\sqrt{gh})t$

which in turn implies that

$u-\sqrt{gh}=\frac{x}{t}$

We also have $R_{+}=u+2\sqrt{gh}=2c_0$ from the $C_{+}$ characteristics. We can solve these equations at each point in $\{x>-c_{0}t\}$. Solving for $u$ and $h$ gives

$h(x,t)=\{\begin{array}{l}\frac{h_0}{9}{(2-\frac{x}{c_{0}t})}^2,-c_{0}t<x<2c_{0}t,\\ h_0,x<-c_{0}t,\end{array}$

$u(x,t)=\{\begin{array}{l}\frac{2}{3}(c_0+\frac{x}{t}),-c_{0}t<x<2c_{0}t,\\ 0,x<-c_{0}t.\end{array}$

Where we have assumed that, since $h=0$ for $x=2c_{0}t,$ the $C_{+}$ characteristic only exist in the region $\{x<2c_{0}t\}$, We will verify this by explicitly calculating them.

Characteristics for the dam break problem, blue for $C_{+}$ and red for $C_{-}$. The solid red lines show the curves $x=-c_{0}t$ and $x=2c_{0}t$ (note we have assumed here that $c_0=1$

It remains to determine the $C_{+}$ characteristic, which originated in $\{x<0\}$, and show they will fill the domain $\{x<2c_{0}t\}$. For $\{x<-c_{0}t\}$, the $C_{+}$ characteristics are straight lines with slope $c_0$ and are given by

$X_{+}(t)=-x_0+c_{0}t,(x_0>0,t<\frac{x_0}{2c_0})$

When $t=\frac{x_0}{2c_0},X_{+}(t)=-c_{0}t$ so that for

$t>\frac{x_0}{2c_0},\frac{d{X}_{+}(t)}{dt}=u+\sqrt{gh}$

and substituting the solution we found for $h$ and $u$

$\frac{d{X}_{+}(t)}{dt}=\frac{4}{3}{c}_0+\frac{X_{+}(t)}{3t}$

Solving this ODE subject to $X_{+}\left(\frac{x_0}{2c_0}\right)=-\frac{x_0}{2}$ gives

$X_{+}(t)=2c_{0}t-3{\left(\frac{x_0}{2}\right)}^{2/3}(c_{0}t{)}^{1/3},$

the equation for a characteristic curve. The curves indeed fill the domain $\{x<2c_{0}t\}$ and all satisfy $\{X_{+}(t)<2c_{0}t\}$. To summarize, the $C^{+}$ characteristics are given by

$X_{+}(t)=\{\begin{array}{l}2c_{0}t-3{\left(\frac{x_0}{2}\right)}^{2/3}(c_{0}t{)}^{1/3},t>x_0/2\\ -x_0+-c_{0}t,0<t<x_0/2\end{array}$

Shocks

For a unique solution two exist there must be a single $C_{+}$ and $C_{-}$ characteristic through each point. When two characteristics of the same kind meet we have a shock forming.

Accelerating Piston

We now consider the problem of water initially at rest occupying the half space $x>0$ which is initially at rest. At $t=0$ the piston at $x=0$ begins to move to the right with constant acceleration $a$ so that the position of the piston is given by $\frac{1}{2}a{t}^2$.

We assume that the $C_{-}$ characteristics which originate in the water at $t=0$ fill the fluid. On these characteristics

$R_{-}=u-2c=-2c_0$

and this condition must hold throughout the fluid. On the $C_{+}$ characteristics we know that $R_{+}=u+2c$ must be a constant and hence on the $C_{+}$ characteristics $u$ and $c$ must be constant and hence the $C_{+}$ characteristics must be straight lines. Note that this does not mean that the $C_{+}$ characteristics have the same slope and there is no requirement that the $C_{-}$ characteristics are straight lines.

The $C_{+}$ characteristic originate from the fluid or from the front of the piston. We consider those which originate from the piston. The $C_{+}$ characteristic which originates from the piston at $t=t_0$ must satisfy

$u+2c=a{t}_0+2c_{\text{plate}}$

where $a{t}_0$ is the velocity of the piston at time $t=t_0$ and $c_{\text{plate}}$ is the speed (related to height) at the plate. We know that $R_{-}=u-2c=-2c_0$ through out the fluid, so that if we solve this at the plate (where $u=a{t}_0$ and $c=c_{\text{plate}}$) then we get $c_{\text{plate}}=a{t}_0/2+c_0$

Therefore, on the $C_{+}$ characteristics $u$ and $c$ are constant and therefore

$\frac{d{X}_{+}}{dt}=u+c=a{t}_0+(\frac{1}{2}a{t}_0+c_0)$

Hence

$X_{+}(t,t_0)=(\frac{3}{2}a{t}_0+c_0)t-c_0{t}_0-a{t}_0^2$

using the condition $X_{+}(t_0)=\frac{1}{2}a{t}_0^2$ (the initial value which comes from the position of the piston at $t=t_0$). The slope of these lines increases and eventually meet to form a shock. We find this point of intersection by considering neighboring characteristics and determining when they first intersect.

$X_{+}(t,t_0+\mathrm{\Delta }t)=X_{+}(t,t_0)+\mathrm{\Delta }t\frac{\partial X_{+}}{\partial t_0}(t,t_0)$

It follows that neighbouring characteristics will meet when

$\frac{\partial X_{+}}{\partial t_0}(t,t_0)=0$

which implies that

$t=\frac{2c_0}{3a}+\frac{4}{3}{t}_0$

The first time that a shock forms is the minimum value of this equation. For this piston example, this occurs when $t_0=0$ and the value of $t$ is $t=2c_0/(3a)$. At this point a shock is formed and we can no longer find a unique solution by following the characteristics.

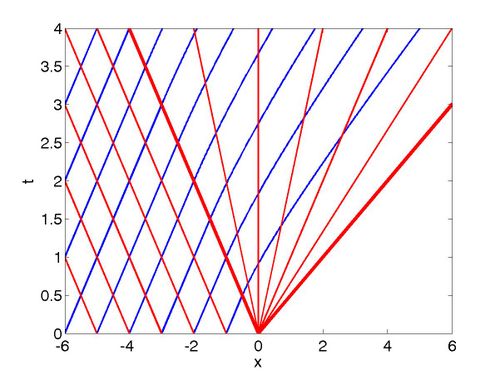
Piston Moving with Constant Velocity

This example is also known as the Moving Wall Problem, and is connected to Shallow Water Bores.

We consider the case of a piston, with positive constant velocity $V$ (which is initially at $x=0$), advancing into a semi-infinite expanse of fluid that is initially at rest with depth $h_0$.

The $C_{+}$ characteristics which originate in the fluid at $t=0$ have slope

$\frac{d{X}_{+}}{dt}=\sqrt{g{h}_0}$

and the $C_{+}$ characteristic which originate at the piston at $t=0$ must satisfy

$\frac{d{X}_{+}}{dt}=\sqrt{g{h}_0}+V$

so that these two characteristics will intersect at $t=0$. Therefore a shock forms immediately and we can track this by determining the speed of the shock

Speed of the shock

We need the conservation equations in integral form to determine the speed of the shock. Conservation of mass, written as an integral is

${\partial }_t{\int }_{x_1}^{x_2}\rho hdx+{\rho uh|}_{x_1}^{x_2}=0$

If the shock is located at $s(t)$ which we assume is located between $x_1$ and $x_2$, then

${\partial }_t{\int }_{x_1}^{x_2}\rho hdx={\partial }_t({\int }_{x_1}^{s(t)}+{\int }_{s(t)}^{x_2})hdx=({\int }_{x_1}^{s(t)}+{\int }_{s(t)}^{x_2}){\partial }_{t}hdx+h^{+}s(t)-h^{+}s(t),$

where $h^{+}$ is the height on the right (positive) side of the jump and $h^{-}$ is the height on the left (negative) side. If we take the limit as $x_1\to x_2$ we then obtain the following identity

$h^{+}{\partial }_{t}s(t)-h^{-}{\partial }_{t}s(t)-u^{+}{h}^{+}+u^{-}{h}^{-}=0$

where $u^{+}$ is the height on the right (positive) side of the jump and $u^{-}$ is the height on the left (negative) side.

We now need to consider the equation for conservation of momentum. In integral form this is

${\partial }_t{\int }_{x_1}^{x_2}\rho hudx={\rho u^{2}h|}_{x_1}^{x_2}+{\int }_0^{h(x_1)}P(x_1,z,t)dz-{\int }_0^{h(x_2)}P(x_2,z,t)dz$

where the pressure $P$ is given by

$P=\rho g(h-z)$

(i.e. we have hydrostatic equilibrium). We can apply a similar argument as before to obtain

$h^{+}{u}^{+}{\partial }_{t}s(t)-h^{-}{u}^{-}{\partial }_{t}s(t)={\left(u^{+}\right)}^2{h}^{+}-{\left(u^{-}\right)}^2{h}^{-}+\frac{1}{2}g{\left(h^{+}\right)}^2-\frac{1}{2}g{\left(h^{-}\right)}^2$

Hydraulic Jump

For a hydraulic jump $s(t)=0$ which means that we must solve

$u^{+}{h}^{+}-u^{-}{h}^{-}=0$

${\left(u^{+}\right)}^2{h}^{+}-{\left(u^{-}\right)}^2{h}^{-}+\frac{1}{2}g{\left(h^{+}\right)}^2-\frac{1}{2}g{\left(h^{-}\right)}^2=0$

If we introduce the variables

$H=\frac{h^{+}}{h^{-}}$

and

$\mathrm{Fr}=\frac{u^{-}}{\sqrt{g{h}^{-}}}$

where $\mathrm{Fr}$ is the Froude number which is equivalent to the Mach number for gas dynamics. Then we obtain

$H^2-1=2{\mathrm{Fr}}^2(1-\frac{1}{H})$

which has a root at H = 1 (not change) or at

$H=\frac{1}{2}(-1\pm \sqrt{1+8{\mathrm{Fr}}^2})$

This only has physically meaningful solution for the positive root and $H>1$ only if $\mathrm{Fr}>1$. This means that we can only obtain a hydraulic jump if the flow is supercritical.

Bore

We now consider a bore, in which the shock wave advances into still water. The fluid must be travelling at the same speed at the piston, so that $u^{-}=V$. We denote the height on the wall side by $h_1$ and the height on the other side must be $h_0$, i.e. $h^{+}=h_0$, $h^{-}=h_1$, $u^{+}=0$. This means that

$h_0{\partial }_{t}s(t)-h_1{\partial }_{t}s(t)+V{h}_1=0$

and

$-h_{1}V{\partial }_{t}s(t)=-{\left(V\right)}^2{h}_1+\frac{1}{2}g{\left(h_0\right)}^2-\frac{1}{2}g{\left(h_1\right)}^2$

which can be solved to obtain the shock speed and the height of the moving fluid.

Below is a video of surfing on the Severn bore, do not believe everything they say. You might also want to check out the Pororoca a tidal bore on the Amazon.