Difference between revisions of "Waves reflecting off a vertical wall"
| Line 3: | Line 3: | ||
{{incident plane wave}} | {{incident plane wave}} | ||
| + | |||
| + | On <math> x = 0 \, </math>: | ||
| + | <center><math> \partial_n\phi = \frac{\partial}{\partial x} | ||
| + | \left( \phi^{\mathrm{I}} + \phi^{mathrm{D}} \right) = 0 </math></center> | ||
| + | where <math>\phi^{mathrm{D}}</math> is the diffraction potential | ||
| + | or | ||
| + | <center><math> - \mathrm{i} k A_I + \mathrm{i} k A_R \Longrightarrow A_R = A_I \equiv A </math></center> | ||
| + | |||
The refl | The refl | ||
| Line 11: | Line 19: | ||
<center><math> \Phi_R = \mathrm{Re} \left \{ \frac{\mathrm{i} gA_R}{\omega} \frac{\cosh k (z+h)}{\cosh k h} | <center><math> \Phi_R = \mathrm{Re} \left \{ \frac{\mathrm{i} gA_R}{\omega} \frac{\cosh k (z+h)}{\cosh k h} | ||
e^{\mathrm{i} k x +\mathrm{i}\omega t} \right \} </math></center> | e^{\mathrm{i} k x +\mathrm{i}\omega t} \right \} </math></center> | ||
| − | + | ||
| − | + | ||
| − | |||
| − | |||
The resulting total velocity potential is | The resulting total velocity potential is | ||
Revision as of 21:49, 3 April 2010
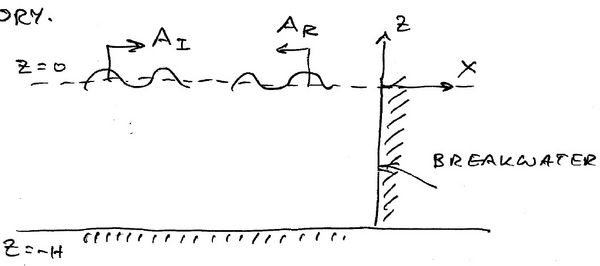
Waves reflecting off a vertical wall is one of the few very important analytical solutions of regular waves interacting with solid boundaries seen in practice. The other is wavemaker theory.
The equation is subject to some radiation conditions at infinity. We assume the following. [math]\displaystyle{ \phi^{\mathrm{I}}\, }[/math] is a plane wave travelling in the [math]\displaystyle{ x }[/math] direction,
where [math]\displaystyle{ A }[/math] is the wave amplitude (in potential) [math]\displaystyle{ \mathrm{i} k }[/math] is the positive imaginary solution of the Dispersion Relation for a Free Surface (note we are assuming that the time dependence is of the form [math]\displaystyle{ \exp(-\mathrm{i}\omega t) }[/math]) and
On [math]\displaystyle{ x = 0 \, }[/math]:
where [math]\displaystyle{ \phi^{mathrm{D}} }[/math] is the diffraction potential or
The refl
The corresponding velocity potentials are
The resulting total velocity potential is
The resulting standing-wave elevation is: