Difference between revisions of "Example Calculations for the KdV and IST"
| Line 1: | Line 1: | ||
{{nonlinear waves course | {{nonlinear waves course | ||
| chapter title = Example Calculations for the KdV and IST | | chapter title = Example Calculations for the KdV and IST | ||
| − | | next chapter = [[ | + | | next chapter = [[Reaction-Diffusion Systems]] |
| − | | previous chapter = [[ | + | | previous chapter = [[Connection betwen KdV and the Schrodinger Equation]] |
}} | }} | ||
Revision as of 01:47, 24 September 2010
| Nonlinear PDE's Course | |
|---|---|
| Current Topic | Example Calculations for the KdV and IST |
| Next Topic | Reaction-Diffusion Systems |
| Previous Topic | Connection betwen KdV and the Schrodinger Equation |
Example1 Delta function potential.
We have already calculated the scattering data for the delta function potential. The scattering data is
The spectral data evolves as
so that
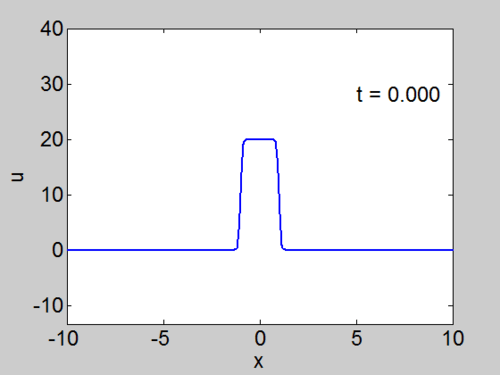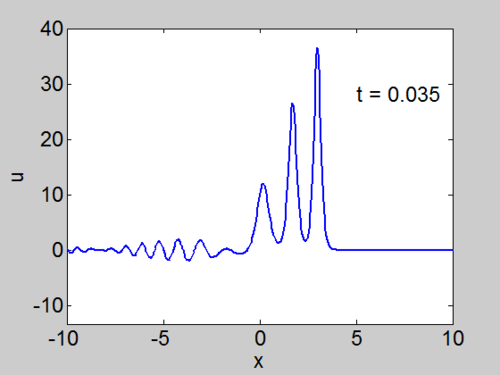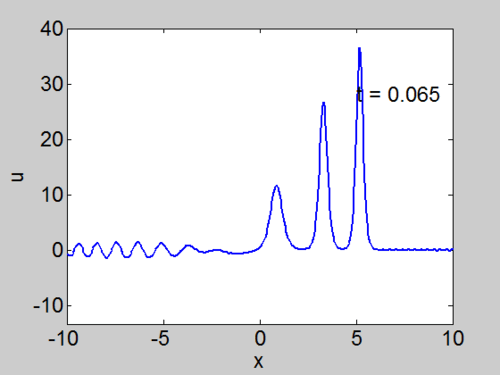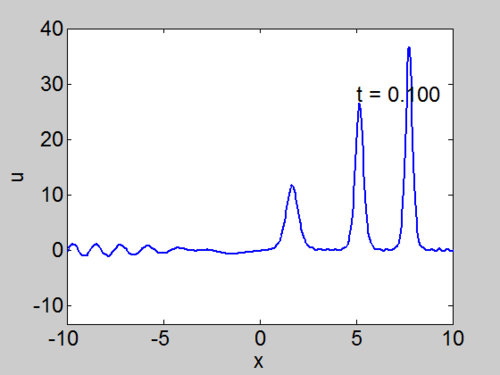
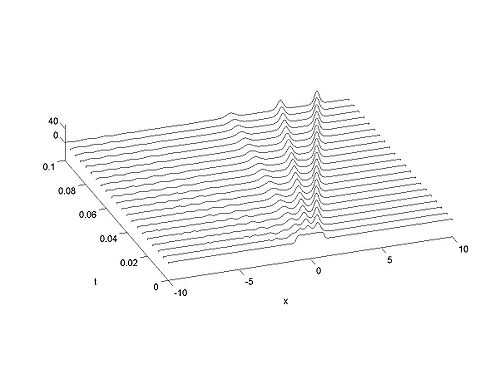
Example 2 A Hat Function
We solve for the case when
For the even solutions we need to solve
where [math]\displaystyle{ \kappa=\sqrt{b-k^{2}} }[/math].
For the odd solutions we need to solve and
Recall that the solitons have amplitude [math]\displaystyle{ 2k_{n}^{2} }[/math] or [math]\displaystyle{ -2\lambda_{n} }[/math]. This can be seen in the height of the solitary waves.
We cannot work with a hat function numerically, because the jump in [math]\displaystyle{ u }[/math] leads to high frequencies which dominate the response.. We can smooth our function by a number of methods. We use here the function [math]\displaystyle{ \tanh\left( x\right) }[/math] so we write
where [math]\displaystyle{ \nu }[/math] is an appropriate constant to make the function increase in value sufficiently rapidly but not too rapidly.
| Animation | Three-dimensional plot. |
|---|---|