Difference between revisions of "Template:Energy contour and preliminaries"
m |
|||
| Line 3: | Line 3: | ||
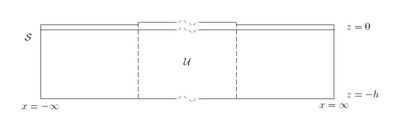
The domain of integration is shown in the figure on the right. We assume that the angle is sufficiently small that we do not get total reflection. | The domain of integration is shown in the figure on the right. We assume that the angle is sufficiently small that we do not get total reflection. | ||
| − | [[Image:energy_schematic.jpg|thumb|right|410px|A diagram depicting the area <math>\mathcal{U}</math> which is bounded by the rectangle <math>\mathcal{S}</math>. | + | [[Image:energy_schematic.jpg|thumb|right|410px|A diagram depicting the area <math>\mathcal{U}</math> which is bounded by the rectangle <math>\mathcal{S}</math>. The rectangle <math>\mathcal{S}</math> is bounded by <math> -h\leq z \leq0</math> and <math>-\infty\leq x \leq \infty</math>]] |
| − | |||
| − | The rectangle <math>\mathcal{S}</math> is bounded by <math> -h\leq z \leq0</math> and | ||
Applying Green's theorem to <math>\phi</math> and its conjugate <math>\phi^*</math> gives | Applying Green's theorem to <math>\phi</math> and its conjugate <math>\phi^*</math> gives | ||
Revision as of 07:31, 24 February 2009
Based on the method used in Evans and Davies 1968, a check can be made to ensure the solutions energy balance. The energy balance equation is derived by applying Green's theorem to [math]\displaystyle{ \phi }[/math] and its conjugate. The domain of integration is shown in the figure on the right. We assume that the angle is sufficiently small that we do not get total reflection.
Applying Green's theorem to [math]\displaystyle{ \phi }[/math] and its conjugate [math]\displaystyle{ \phi^* }[/math] gives
where [math]\displaystyle{ n }[/math] denotes the outward plane normal to the boundary and [math]\displaystyle{ l }[/math] denotes the plane parallel to the boundary. As [math]\displaystyle{ \phi }[/math] and [math]\displaystyle{ \phi^* }[/math] satisfy the Laplace's equation, the left hand side of the Green theorem equation vanishes so that it reduces to