Difference between revisions of "Wavemaker Theory"
Mike smith (talk | contribs) (remove repeated formula, correct x=0 substitution, mention imaginery k0) |
|||
| Line 7: | Line 7: | ||
= Introduction = | = Introduction = | ||
| − | [[Image:Wavemaker.jpg | + | [[Image:Wavemaker.jpg|600px|Wavemaker]] |
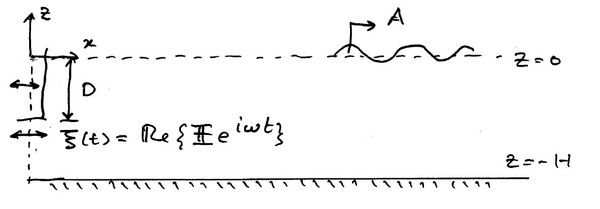
We will derive the potential in a two-dimensional wavetank due the motion of the wavemaker. The method is based on the [[:Category:Eigenfunction Matching Method|Eigenfunction Matching Method]]. | We will derive the potential in a two-dimensional wavetank due the motion of the wavemaker. The method is based on the [[:Category:Eigenfunction Matching Method|Eigenfunction Matching Method]]. | ||
A paddle is undergoing small amplitude horizontal oscillations with displacement | A paddle is undergoing small amplitude horizontal oscillations with displacement | ||
<center><math> \xi (t) = \mathfrak{Re} \left \{\frac{1}{i\omega} f(z) e^{i\omega t} \right \} </math></center> | <center><math> \xi (t) = \mathfrak{Re} \left \{\frac{1}{i\omega} f(z) e^{i\omega t} \right \} </math></center> | ||
| − | where <math> f(z) </math> is assumed known. Since the time <math>t=0</math> is arbitrary we can assume that | + | where <math> f(z) \, </math> is assumed known. Since the time <math>t=0 \,</math> is arbitrary we can assume that |
| − | <math>f(z)</math> is real but this is not necessary. | + | <math>f(z)\,</math> is real but this is not necessary. |
Because the oscillations are small the [[Linear and Second-Order Wave Theory| linear equations]] apply (which will be given formally below). | Because the oscillations are small the [[Linear and Second-Order Wave Theory| linear equations]] apply (which will be given formally below). | ||
This excitation creates plane progressive waves with amplitude <math> A \, </math> down the tank. The principal objective of wavemaker theory is to determine <math> A \, </math> | This excitation creates plane progressive waves with amplitude <math> A \, </math> down the tank. The principal objective of wavemaker theory is to determine <math> A \, </math> | ||
| Line 20: | Line 20: | ||
= Expansion of the solution = | = Expansion of the solution = | ||
| − | |||
| − | |||
| − | |||
| − | |||
Let the total velocity potential be | Let the total velocity potential be | ||
<center><math> \Phi(x,z,t) = \mathfrak{Re} \left \{ \phi(x,z) e^{i\omega t} \right \} </math></center>. | <center><math> \Phi(x,z,t) = \mathfrak{Re} \left \{ \phi(x,z) e^{i\omega t} \right \} </math></center>. | ||
| Line 29: | Line 25: | ||
The water is assumed to have | The water is assumed to have | ||
constant finite depth <math>h</math> and the <math>z</math>-direction points vertically | constant finite depth <math>h</math> and the <math>z</math>-direction points vertically | ||
| − | upward with the water surface at <math>z=0</math> and the sea floor at <math>z=-h</math>. The | + | upward with the water surface at <math>z=0 \,</math> and the sea floor at <math>z=-h \,</math>. The |
boundary value problem can therefore be expressed as | boundary value problem can therefore be expressed as | ||
<center> | <center> | ||
| Line 41: | Line 37: | ||
</math> | </math> | ||
</center> | </center> | ||
| − | <center><math> | + | <center> |
| + | <math> | ||
\partial_z\phi=\alpha\phi, \,\, z=0,\,x>0, | \partial_z\phi=\alpha\phi, \,\, z=0,\,x>0, | ||
| − | </math></center> | + | </math> |
| + | </center> | ||
<center> | <center> | ||
<math> | <math> | ||
| Line 58: | Line 56: | ||
= Expansion in Eigenfunctions = | = Expansion in Eigenfunctions = | ||
| − | The wavemaker velocity potential <math> \phi </math> can be expressed simply in terms of eigenfunctions | + | The wavemaker velocity potential <math> \phi \,</math> can be expressed simply in terms of eigenfunctions |
<center><math> \phi = \sum_{n=0}^{\infty} a_n \phi_n (x) e^{-k_n x} </math></center> | <center><math> \phi = \sum_{n=0}^{\infty} a_n \phi_n (x) e^{-k_n x} </math></center> | ||
| − | and we can solve for the coefficients by matching at <math>x=0</math> | + | and we can solve for the coefficients by matching at <math>x=0 \,</math> |
| − | <center><math> \left. \phi_x(z) \right|_{x=0} = \sum_{n=0}^{\infty} -k_n a_n \phi_n (x) | + | <center><math> \left. \phi_x(z) \right|_{x=0} = \sum_{n=0}^{\infty} -k_n a_n \phi_n (x) = f(z) |
</math></center> | </math></center> | ||
| Line 72: | Line 70: | ||
== Far Field Wave == | == Far Field Wave == | ||
| − | One of the primary objecives of wavemaker theory is to determine the far-field wave amplitude <math> A \, </math> in terms of <math> f(z) </math>. | + | One of the primary objecives of wavemaker theory is to determine the far-field wave amplitude <math> A \, </math> in terms of <math> f(z) \, </math>. |
The far-field wave component representing progagating waves is given by: | The far-field wave component representing progagating waves is given by: | ||
<center><math> \phi_w = a_0 \frac{\cos k_0(z+h)}{\cos k_0 h } e^{-k_0 x} </math></center> | <center><math> \phi_w = a_0 \frac{\cos k_0(z+h)}{\cos k_0 h } e^{-k_0 x} </math></center> | ||
| − | We therefore obtain the complex amplitude of the propagating wave at infinity, namely modulus and phase, in terms of the wave maker displacement <math> f(z) </math>. | + | Note that <math> k_0 \, </math> is imaginery. We therefore obtain the complex amplitude of the propagating wave at infinity, namely modulus and phase, in terms of the wave maker displacement <math> f(z) \, </math>. |
| − | For what type of <math> f(z) </math> are the non-wavelike modes zero? It is easy to verify by virtue of orthogonality that | + | For what type of <math> f(z) \, </math> are the non-wavelike modes zero? It is easy to verify by virtue of orthogonality that |
<center><math> f(z) \ \sim \ \phi_0 (z) </math></center> | <center><math> f(z) \ \sim \ \phi_0 (z) </math></center> | ||
Revision as of 02:20, 27 February 2009
| Wave and Wave Body Interactions | |
|---|---|
| Current Chapter | Wavemaker Theory |
| Next Chapter | Translating Coordinate Systems |
| Previous Chapter | Wave Momentum Flux |
Introduction
We will derive the potential in a two-dimensional wavetank due the motion of the wavemaker. The method is based on the Eigenfunction Matching Method. A paddle is undergoing small amplitude horizontal oscillations with displacement
where [math]\displaystyle{ f(z) \, }[/math] is assumed known. Since the time [math]\displaystyle{ t=0 \, }[/math] is arbitrary we can assume that [math]\displaystyle{ f(z)\, }[/math] is real but this is not necessary. Because the oscillations are small the linear equations apply (which will be given formally below). This excitation creates plane progressive waves with amplitude [math]\displaystyle{ A \, }[/math] down the tank. The principal objective of wavemaker theory is to determine [math]\displaystyle{ A \, }[/math] as a function of [math]\displaystyle{ \omega, f(z) \, }[/math] and [math]\displaystyle{ h \, }[/math]. Time-dependent wavemaker theories can also be developed.
Expansion of the solution
Let the total velocity potential be
.
This gives us a Frequency Domain Problem. The water is assumed to have constant finite depth [math]\displaystyle{ h }[/math] and the [math]\displaystyle{ z }[/math]-direction points vertically upward with the water surface at [math]\displaystyle{ z=0 \, }[/math] and the sea floor at [math]\displaystyle{ z=-h \, }[/math]. The boundary value problem can therefore be expressed as
[math]\displaystyle{ \Delta\phi=0, \,\, -h\lt z\lt 0,\,x\gt 0, }[/math]
[math]\displaystyle{ \phi_{z}=0, \,\, z=-h, }[/math]
[math]\displaystyle{ \partial_z\phi=\alpha\phi, \,\, z=0,\,x\gt 0, }[/math]
[math]\displaystyle{ \left. \partial_x\phi \right|_{x=0} = \partial_t \xi = f(z). }[/math]
We must also apply the Sommerfeld Radiation Condition as [math]\displaystyle{ x\rightarrow\infty }[/math]. This essentially implies that the only wave at infinity is propagating away.
Separation of variables for a free surface
We use separation of variables
We express the potential as
[math]\displaystyle{ \phi(x,z) = X(x)Z(z)\, }[/math]
and then Laplace's equation becomes
[math]\displaystyle{ \frac{X^{\prime\prime}}{X} = - \frac{Z^{\prime\prime}}{Z} = k^2 }[/math]
The separation of variables equation for deriving free surface eigenfunctions is as follows:
[math]\displaystyle{ Z^{\prime\prime} + k^2 Z =0. }[/math]
subject to the boundary conditions
[math]\displaystyle{ Z^{\prime}(-h) = 0 }[/math]
and
[math]\displaystyle{ Z^{\prime}(0) = \alpha Z(0) }[/math]
We can then use the boundary condition at [math]\displaystyle{ z=-h \, }[/math] to write
[math]\displaystyle{ Z = \frac{\cos k(z+h)}{\cos kh} }[/math]
where we have chosen the value of the coefficent so we have unit value at [math]\displaystyle{ z=0 }[/math]. The boundary condition at the free surface ([math]\displaystyle{ z=0 \, }[/math]) gives rise to:
which is the Dispersion Relation for a Free Surface
The above equation is a transcendental equation. If we solve for all roots in the complex plane we find that the first root is a pair of imaginary roots. We denote the imaginary solutions of this equation by [math]\displaystyle{ k_{0}=\pm ik \, }[/math] and the positive real solutions by [math]\displaystyle{ k_{m} \, }[/math], [math]\displaystyle{ m\geq1 }[/math]. The [math]\displaystyle{ k \, }[/math] of the imaginary solution is the wavenumber. We put the imaginary roots back into the equation above and use the hyperbolic relations
[math]\displaystyle{ \cos ix = \cosh x, \quad \sin ix = i\sinh x, }[/math]
to arrive at the dispersion relation
[math]\displaystyle{ \alpha = k\tanh kh. }[/math]
We note that for a specified frequency [math]\displaystyle{ \omega \, }[/math] the equation determines the wavenumber [math]\displaystyle{ k \, }[/math].
Finally we define the function [math]\displaystyle{ Z(z) \, }[/math] as
[math]\displaystyle{ \chi_{m}\left( z\right) =\frac{\cos k_{m}(z+h)}{\cos k_{m}h},\quad m\geq0 }[/math]
as the vertical eigenfunction of the potential in the open water region. From Sturm-Liouville theory the vertical eigenfunctions are orthogonal. They can be normalised to be orthonormal, but this has no advantages for a numerical implementation. It can be shown that
[math]\displaystyle{ \int\nolimits_{-h}^{0}\chi_{m}(z)\chi_{n}(z) \mathrm{d} z=A_{n}\delta_{mn} }[/math]
where
[math]\displaystyle{ A_{n}=\frac{1}{2}\left( \frac{\cos k_{n}h\sin k_{n}h+k_{n}h}{k_{n}\cos ^{2}k_{n}h}\right). }[/math]
Expansion in Eigenfunctions
The wavemaker velocity potential [math]\displaystyle{ \phi \, }[/math] can be expressed simply in terms of eigenfunctions
and we can solve for the coefficients by matching at [math]\displaystyle{ x=0 \, }[/math]
It follows that
Far Field Wave
One of the primary objecives of wavemaker theory is to determine the far-field wave amplitude [math]\displaystyle{ A \, }[/math] in terms of [math]\displaystyle{ f(z) \, }[/math]. The far-field wave component representing progagating waves is given by:
Note that [math]\displaystyle{ k_0 \, }[/math] is imaginery. We therefore obtain the complex amplitude of the propagating wave at infinity, namely modulus and phase, in terms of the wave maker displacement [math]\displaystyle{ f(z) \, }[/math].
For what type of [math]\displaystyle{ f(z) \, }[/math] are the non-wavelike modes zero? It is easy to verify by virtue of orthogonality that
Unfortunately this is not a "practical" displacement since [math]\displaystyle{ \phi_0 (z) \, }[/math] depends on [math]\displaystyle{ \omega\, }[/math], so one would need to build a flexible paddle.
Matlab Code
A program to calculate the coefficients for the wave maker problems can be found here wavemaker.m
Additional code
This program requires dispersion_free_surface.m to run
This article is based in part on the MIT open course notes and the original article can be found here
Ocean Wave Interaction with Ships and Offshore Energy Systems