Wavemaker Theory

Wave and Wave Body Interactions
Current Chapter	Wavemaker Theory
Next Chapter	Translating Coordinate Systems
Previous Chapter	Wave Momentum Flux

Introduction

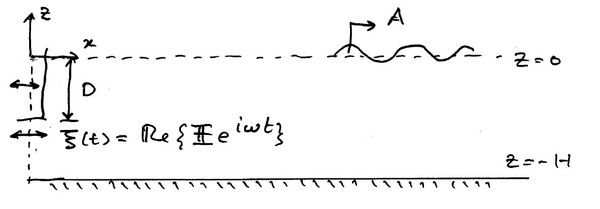
We will derive the potential in a two-dimensional wavetank due the motion of the wavemaker. The method is based on the Eigenfunction Matching Method. A paddle is undergoing small amplitude horizontal oscillations with displacement

[math]\displaystyle{ \xi (t) = \mathrm{Re} \left \{\frac{1}{i\omega} f(z) e^{i\omega t} \right \} }[/math]

where [math]\displaystyle{ f(z) \, }[/math] is assumed known. Since the time [math]\displaystyle{ t=0 \, }[/math] is arbitrary we can assume that [math]\displaystyle{ f(z)\, }[/math] is real but this is not necessary. Because the oscillations are small the linear equations apply (which will be given formally below). This excitation creates plane progressive waves with amplitude [math]\displaystyle{ A \, }[/math] down the tank. The principal objective of wavemaker theory is to determine [math]\displaystyle{ A \, }[/math] as a function of [math]\displaystyle{ \omega, f(z) \, }[/math] and [math]\displaystyle{ h \, }[/math]. Time-dependent wavemaker theories can also be developed.

Expansion of the solution

Let the total velocity potential be

[math]\displaystyle{ \Phi(x,z,t) = \mathrm{Re} \left \{ \phi(x,z) e^{i\omega t} \right \} }[/math]

.

This gives us a Frequency Domain Problem. The water is assumed to have constant finite depth [math]\displaystyle{ h \, }[/math] and the [math]\displaystyle{ z \, }[/math]-direction points vertically upward with the water surface at [math]\displaystyle{ z=0 \, }[/math] and the sea floor at [math]\displaystyle{ z=-h \, }[/math]. The boundary value problem can therefore be expressed as

[math]\displaystyle{ \Delta\phi=0, \,\, -h\lt z\lt 0,\,x\gt 0, }[/math]

[math]\displaystyle{ \phi_{z}=0, \,\, z=-h, }[/math]

[math]\displaystyle{ \partial_z\phi=\alpha\phi, \,\, z=0,\,x\gt 0, }[/math]

[math]\displaystyle{ \left. \partial_x\phi \right|_{x=0} = \partial_t \xi = f(z). }[/math]

We must also apply the Sommerfeld Radiation Condition as [math]\displaystyle{ x\rightarrow\infty }[/math]. This essentially implies that the only wave at infinity is propagating away.

Separation of variables for a free surface

We use separation of variables

We express the potential as

[math]\displaystyle{ \phi(x,z) = X(x)Z(z)\, }[/math]

and then Laplace's equation becomes

[math]\displaystyle{ \frac{X^{\prime\prime}}{X} = - \frac{Z^{\prime\prime}}{Z} = k^2 }[/math]

The separation of variables equation for deriving free surface eigenfunctions is as follows:

[math]\displaystyle{ Z^{\prime\prime} + k^2 Z =0. }[/math]

subject to the boundary conditions

[math]\displaystyle{ Z^{\prime}(-h) = 0 }[/math]

and

[math]\displaystyle{ Z^{\prime}(0) = \alpha Z(0) }[/math]

We can then use the boundary condition at [math]\displaystyle{ z=-h \, }[/math] to write

[math]\displaystyle{ Z = \frac{\cos k(z+h)}{\cos kh} }[/math]

where we have chosen the value of the coefficent so we have unit value at [math]\displaystyle{ z=0 }[/math]. The boundary condition at the free surface ([math]\displaystyle{ z=0 \, }[/math]) gives rise to:

[math]\displaystyle{ k\tan\left( kh\right) =-\alpha \, }[/math]

which is the Dispersion Relation for a Free Surface

The above equation is a transcendental equation. If we solve for all roots in the complex plane we find that the first root is a pair of imaginary roots. We denote the imaginary solutions of this equation by [math]\displaystyle{ k_{0}=\pm ik \, }[/math] and the positive real solutions by [math]\displaystyle{ k_{m} \, }[/math], [math]\displaystyle{ m\geq1 }[/math]. The [math]\displaystyle{ k \, }[/math] of the imaginary solution is the wavenumber. We put the imaginary roots back into the equation above and use the hyperbolic relations

[math]\displaystyle{ \cos ix = \cosh x, \quad \sin ix = i\sinh x, }[/math]

to arrive at the dispersion relation

[math]\displaystyle{ \alpha = k\tanh kh. }[/math]

We note that for a specified frequency [math]\displaystyle{ \omega \, }[/math] the equation determines the wavenumber [math]\displaystyle{ k \, }[/math].

Finally we define the function [math]\displaystyle{ Z(z) \, }[/math] as

[math]\displaystyle{ \chi_{m}\left( z\right) =\frac{\cos k_{m}(z+h)}{\cos k_{m}h},\quad m\geq0 }[/math]

as the vertical eigenfunction of the potential in the open water region. From Sturm-Liouville theory the vertical eigenfunctions are orthogonal. They can be normalised to be orthonormal, but this has no advantages for a numerical implementation. It can be shown that

[math]\displaystyle{ \int\nolimits_{-h}^{0}\chi_{m}(z)\chi_{n}(z) \mathrm{d} z=A_{n}\delta_{mn} }[/math]

where

[math]\displaystyle{ A_{n}=\frac{1}{2}\left( \frac{\cos k_{n}h\sin k_{n}h+k_{n}h}{k_{n}\cos ^{2}k_{n}h}\right). }[/math]

Expansion in Eigenfunctions

The wavemaker velocity potential [math]\displaystyle{ \phi \, }[/math] can be expressed simply in terms of eigenfunctions

[math]\displaystyle{ \phi = \sum_{n=0}^{\infty} a_n \phi_n (z) e^{-k_n x} }[/math]

and we can solve for the coefficients by matching at [math]\displaystyle{ x=0 \, }[/math]

[math]\displaystyle{ \left. \phi_x \right|_{x=0} = \sum_{n=0}^{\infty} -k_n a_n \phi_n (z) = f(z) }[/math]

It follows that

[math]\displaystyle{ a_n = -\frac{1}{k_n A_n} \int_{-h}^0 \phi_n(z) f(z)\mathrm{d}z }[/math]

Far Field Wave

One of the primary objecives of wavemaker theory is to determine the far-field wave amplitude [math]\displaystyle{ A \, }[/math] in terms of [math]\displaystyle{ f(z) \, }[/math]. The far-field wave component representing progagating waves is given by:

[math]\displaystyle{ \phi_w = a_0 \frac{\cos k_0(z+h)}{\cos k_0 h } e^{-k_0 x} }[/math]

Note that [math]\displaystyle{ k_0 \, }[/math] is imaginery. We therefore obtain the complex amplitude of the propagating wave at infinity, namely modulus and phase, in terms of the wave maker displacement [math]\displaystyle{ f(z) \, }[/math].

For what type of [math]\displaystyle{ f(z) \, }[/math] are the non-wavelike modes zero? It is easy to verify by virtue of orthogonality that

[math]\displaystyle{ f(z) \ \sim \ \phi_0 (z) }[/math]

Unfortunately this is not a "practical" displacement since [math]\displaystyle{ \phi_0 (z) \, }[/math] depends on [math]\displaystyle{ \omega\, }[/math], so one would need to build a flexible paddle.

Matlab Code

A program to calculate the coefficients for the wave maker problems can be found here wavemaker.m

Additional code

This program requires dispersion_free_surface.m to run

---

This article is based in part on the MIT open course notes and the original article can be found here

Ocean Wave Interaction with Ships and Offshore Energy Systems Categroy:Complete Pages