Linear Plane Progressive Regular Waves

Wave and Wave Body Interactions
Current Chapter	Linear Plane Progressive Regular Waves
Next Chapter	Wave Energy Density and Flux
Previous Chapter	Linear and Second-Order Wave Theory

Introduction

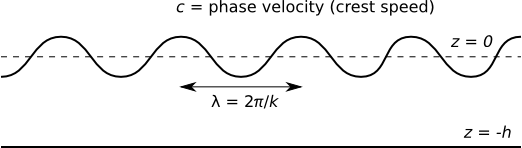
Regular time-harmonic linear plane progressive waves are the fundamental building block in describing the propagation of surface wave disturbances in a deterministic and stochastic setting and in predicting the response of floating structures in a seastate.

Equations

We derive the solution for regular time-harmonic linear plane progressive waves for the first order potential in water of constant Finite Depth. The equations of motion in the time domain are Laplace's equation through out the fluid

[math]\displaystyle{ \Delta\Phi\left( \mathbf{x,}t\right) =0,\ \ \mathbf{x}\in\Omega. }[/math]

At the bottom surface we have no flow

[math]\displaystyle{ \partial_{n}\Phi=0,\ \ z=-h. }[/math]

At the free surface we have the kinematic condition

[math]\displaystyle{ \partial_{t}\zeta=\partial_{n}\Phi,\ \ z=0,\ x\in \partial\Omega_{F}, }[/math]

and the dynamic condition (the linearized Bernoulli equation)

[math]\displaystyle{ \partial_{t}\Phi = -g\zeta ,\ \ z=0,\ x\in \partial\Omega_{F}. }[/math]

It turns out that if the water is sufficiently deep the wave does not feel any effect from the sea floor and we can make the Infinite Depth assumption.

Propagating Wave

Propagating Wave

There are a number of ways to derive the propagating wave solution, but the simplest is to define the free surface elevation apriori as

[math]\displaystyle{ \zeta (x,t) = A \cos ( \omega t - k x) = A \mathbf{Re} \{ e^{-ikx+i\omega t} \} }[/math]

where A is an apriori known wave amplitude and the wave frequency and wave number [math]\displaystyle{ (\omega, k) \, }[/math] pair have the same definitions as in all wave propagation problems, namely:

[math]\displaystyle{ T = \frac{2\pi}{\omega} = \mbox{Wave Period} }[/math] [math]\displaystyle{ \lambda = \frac{2\pi}{k} = \mbox{Wave Length} }[/math] [math]\displaystyle{ c= \frac{\omega}{k} = \mbox{Wave Phase Velocity} }[/math]

The relation between [math]\displaystyle{ \omega \, }[/math] and [math]\displaystyle{ k \, }[/math] is known as the dispersion relation often written in the form

[math]\displaystyle{ \omega = f (k) \,. }[/math]

[math]\displaystyle{ f(k) \, }[/math] depends on the physics of the wave propagation problem under study, surface ocean waves are dispersive since [math]\displaystyle{ f(k)\, }[/math] is a non linear function of [math]\displaystyle{ k \, }[/math] as we will shortly show.

Expression in terms of velocity potential

We also assume that Frequency Domain Problem with frequency [math]\displaystyle{ \omega }[/math] and we assume that all variables are proportional to [math]\displaystyle{ \exp(-\mathrm{i}\omega t)\, }[/math] The water motion is represented by a velocity potential which is denoted by [math]\displaystyle{ \phi\, }[/math] so that

[math]\displaystyle{ \Phi(\mathbf{x},t) = \mathrm{Re} \left\{\phi(\mathbf{x},\omega)e^{-\mathrm{i} \omega t}\right\}. }[/math]

The equations are the following

[math]\displaystyle{ \begin{align} \Delta\phi &=0, &-h\lt z\lt 0,\,\,\mathbf{x} \in \Omega \\ \partial_z\phi &= 0, &z=-h, \\ \partial_z \phi &= \alpha \phi, &z=0,\,\,\mathbf{x} \in \partial \Omega_{\mathrm{F}}, \end{align} }[/math]

(note that the last expression can be obtained from combining the expressions:

[math]\displaystyle{ \begin{align} \partial_z \phi &= -\mathrm{i} \omega \zeta, &z=0,\,\,\mathbf{x} \in \partial \Omega_{\mathrm{F}}, \\ \mathrm{i} \omega \phi &= g\zeta, &z=0,\,\,\mathbf{x} \in \partial \Omega_{\mathrm{F}}, \end{align} }[/math]

where [math]\displaystyle{ \alpha = \omega^2/g \, }[/math])

[math]\displaystyle{ \partial_n\phi = \mathcal{L}\phi, \quad \mathbf{x}\in\partial\Omega_B, }[/math]

where [math]\displaystyle{ \mathcal{L} }[/math] is a linear operator which relates the normal and potential on the body surface through the physics of the body.

The equation is subject to some radiation conditions at infinity. We assume the following. [math]\displaystyle{ \phi^{\mathrm{I}}\, }[/math] is a plane wave travelling in the [math]\displaystyle{ x }[/math] direction,

[math]\displaystyle{ \phi^{\mathrm{I}}(x,z)=A \phi_0(z) e^{\mathrm{i} k x} \, }[/math]

where [math]\displaystyle{ A }[/math] is the wave amplitude (in potential) [math]\displaystyle{ \mathrm{i} k }[/math] is the positive imaginary solution of the Dispersion Relation for a Free Surface (note we are assuming that the time dependence is of the form [math]\displaystyle{ \exp(-\mathrm{i}\omega t) }[/math]) and

[math]\displaystyle{ \phi_0(z) =\frac{\cosh k(z+h)}{\cosh k h} }[/math]

In two-dimensions the Sommerfeld Radiation Condition is

[math]\displaystyle{ \left( \frac{\partial}{\partial|x|} - \mathrm{i} k \right) (\phi-\phi^{\mathrm{{I}}})=0,\;\mathrm{{as\;}}|x|\rightarrow\infty\mathrm{.} }[/math]

where [math]\displaystyle{ \phi^{\mathrm{{I}}} }[/math] is the incident potential.

In three-dimensions the Sommerfeld Radiation Condition is

[math]\displaystyle{ \sqrt{|\mathbf{r}|}\left( \frac{\partial}{\partial|\mathbf{r}|} - \mathrm{i} k \right) (\phi-\phi^{\mathrm{{I}}})=0,\;\mathrm{{as\;}}|\mathbf{r}|\rightarrow\infty\mathrm{.} }[/math]

where [math]\displaystyle{ \phi^{\mathrm{{I}}} }[/math] is the incident potential. By virtue of the definition of the wave elevation of a plane progressive regular wave, we seek a compatible definition of the respective velocity potential. Let:

[math]\displaystyle{ \Phi = A \mathbf{Re} \{ \phi (x,z) e^{i\omega t} \} }[/math]

The problem reduces to the definition of [math]\displaystyle{ \phi(x,z) \, }[/math] and the derivation of the appropriate dispersion relation between [math]\displaystyle{ \omega \, }[/math] and [math]\displaystyle{ k \, }[/math] so that the linear boundary value problem is satisfied. Remember that the equation requires that we consider the fluid potential rather than simply the free surface.

Before proceeding with the algebra, certain underlying principles are always at work:

• Linear system theory states that when the input signal is [math]\displaystyle{ e^{i \omega t} \, }[/math] the output signal must also be harmonic and with the same frequency.

• We assume that a solution always exists, otherwise the statement of the physical and/or mathematical boundary value problem is flawed. If we can find a solution in most cases it is the solution. So simply try out solutions that may make sense from the physical point of view.

• If the boundary value problem is satisfied by a complex velocity potential then it is also satisfied by its real and imaginary parts.

It follows upon substitution in the boundary value problem satisfied by [math]\displaystyle{ \Phi (x,z,t) \, }[/math] that [math]\displaystyle{ \phi (x,z) \, }[/math] is subject to:

[math]\displaystyle{ \begin{cases} - \omega^2 \phi + g \partial_z\phi = 0,& z=0 \\ \nabla^2\phi = \partial^2_x \phi + \partial^2_z\phi = 0,& -h\lt z\lt 0 \\ \partial_z\phi = 0,& z=-h \end{cases} }[/math]

In our case we will first derive the boundary value problem satisfied by the complex potential [math]\displaystyle{ \phi(x,z) \, }[/math] and then we will try the plausible representation:

[math]\displaystyle{ \phi (x,z) = Z(z) e^{- i k x} \, }[/math]

More detailed mathematical explanation of this can be found Eigenfunction Matching

It follows that [math]\displaystyle{ Z(z) \, }[/math] is subject to:

[math]\displaystyle{ \begin{cases} - \omega^2 Z + g \partial_z Z = 0,& z=0 \\ \partial^2_z Z - k^2Z = 0,& -h\lt z\lt 0 \\ \partial_z Z = 0,& z=-h \end{cases} }[/math]

We can verify by simple substitution that

[math]\displaystyle{ Z(z) = \frac{ig}{\omega} \frac{\cosh k(z+h)}{\cosh k h} }[/math]

satisfies the field equation [math]\displaystyle{ \partial^2_z Z - k^2 \psi = 0 \, }[/math], the seafloor condition [math]\displaystyle{ \partial_z Z =0, \, z=-h }[/math], and the free surface condition, only when

[math]\displaystyle{ \omega^2 = g k \tanh kh \, }[/math]

or

[math]\displaystyle{ \omega = \{ gk \tanh k h \}^{1/2} \, }[/math]

So by enforcing the free surface condition we have derived the Dispersion Relation for a Free Surface in Finite Depth.

The resulting plane progressive wave velocity potential takes the form:

[math]\displaystyle{ \phi_1 (x,z,t) = A \ \mathbf{Re} \left\{ \frac{ig}{\omega} \frac{\cosh k (z+h)}{\cosh k h} e^{ - i k x + i \omega t} \right\} }[/math]

This derivation is discussed in more mathematical depth in Eigenfunction Matching Method

Displacement and Pressure

The surface displacement [math]\displaystyle{ \zeta }[/math] for a plane wave follows from

[math]\displaystyle{ \zeta = - \frac{1}{g} \left. \partial_t \phi \right|_{z=0} = A \ \mathbf{Re} \{ e^{-ikx+i\omega t} \} }[/math]

The corresponding flow velocity at some point [math]\displaystyle{ \mathbf{x} = (x,z) }[/math] in the fluid domain or on [math]\displaystyle{ z=0, z=-h \, }[/math] is simply given by

[math]\displaystyle{ \mathbf{v} = \nabla \phi }[/math]

This equation leads to a harmonic solution for the particle trajectories which are ellipses (becoming circles as the depth becomes infinite. If second-order effects are included, the particles under a plane progressive waves also undergo a steady-state drift known as the stokes drift.

The linear hydrodynamic pressure due to the plane progressive wave, which must be added to the hydrostatic, is

[math]\displaystyle{ P = \rho \frac{\partial \phi}{\partial t} = \mathbf{Re} \left\{ \rho g A \frac{\cosh k (z+h)}{\cosh k h } e^{-ikx + i\omega t} \right\} }[/math]

Dispersion Relation for a Free Surface in Deep and Shallow Waters

In Finite Depth

[math]\displaystyle{ \omega^2 = gk\tanh kh \, }[/math]

which is a nonlinear algebraic equation for [math]\displaystyle{ \omega\, }[/math] as a function of [math]\displaystyle{ k\, }[/math] which has a unique positive real solution as can be shown graphically. It also has imaginary roots which are important in many application (see Dispersion Relation for a Free Surface and Eigenfunction Matching Method) The unique positive real root [math]\displaystyle{ k \, }[/math] can only be found numerically. Yet it always exists and the iterative methods that may be implemented always converge rapidly. In deep water, [math]\displaystyle{ h \to \infty }[/math] and therefore

[math]\displaystyle{ \tanh kh \to 1 }[/math]

which in turn implies the deep water dispersion relation

[math]\displaystyle{ \omega^2 = g k \,. }[/math]

The phase speed is given by

[math]\displaystyle{ c = \frac{\omega}{k} = \frac{\omega}{\omega^2/g} = \frac{g}{\omega} = \frac{g}{2\pi/T} = \frac{gT}{2\pi} }[/math]

So the speed of the crest of a wave with period [math]\displaystyle{ \,T = 10 \mathrm{secs} }[/math] is approximately [math]\displaystyle{ 15.6 \,\mathrm{m/s} }[/math] or about 30 knots!

Often we need a quick estimate of the wavelength of a water wave the period of which we can measure accurately with a stop watch. We proceed as follows:

[math]\displaystyle{ c = \frac{\omega}{k} = \frac{\lambda}{T} \ \Longrightarrow \ \frac{\lambda}{T} = \frac{g}{\omega} = \frac{g}{2\pi/T} \ \Longrightarrow \ \lambda = \frac{gT^2}{2\pi} \simeq T^2 + \frac{1}{2} T^2 }[/math]

(by definition the phase speed is the ration of the wave length over the period, or the time it takes for a crest to travel that distance). So the wave length of a deep water wave in m is approximately the square of its period is seconds plus half that amount. So a wave with period [math]\displaystyle{ T=10 }[/math] secs is about [math]\displaystyle{ 150 m }[/math] long.

In the limit of Shallow Depth [math]\displaystyle{ kh \to 0 }[/math] which in turn implies that

[math]\displaystyle{ \tanh kh \simeq kh }[/math]

It therefore follows that

[math]\displaystyle{ \omega^2 = gk (kh) \ \Longrightarrow \ \frac{\omega^2}{k^2} = gh }[/math]

or

[math]\displaystyle{ \frac{\omega}{k} = c = \sqrt{gh} }[/math]

Thus, according to linear theory shallow water waves become non dispersive as is the case with acoustic waves. Unfortunately, nonlinear effects become more important as waves propagate from deep to shallow water (because the wave amplidute rises). Solitons and wave breaking are some manifestations of nonlinearity.

The transition from deep to finite depth wave effects occurs for values of [math]\displaystyle{ kh \le \pi }[/math]. This is because

[math]\displaystyle{ \tanh \pi \simeq 1 }[/math]

and for [math]\displaystyle{ kh = \pi \ \Longrightarrow \ \frac{2\pi h}{\lambda} = \pi \ \Longrightarrow \ \frac{h}{\lambda} = \frac{1}{2} }[/math] so for [math]\displaystyle{ \frac{h}{\lambda} \gt \frac{1}{2} }[/math] or [math]\displaystyle{ kh \gt \pi }[/math] we are effectively dealing with Infinite Depth. This means that for most of the world ocean and wave conditions the water depth may be approximate as infinite.

---

This article is based on the MIT open course notes and the original article can be found here

Ocean Wave Interaction with Ships and Offshore Energy Systems