Wave Momentum Flux

Introduction

The momentum is important to determine the forces.

Momentum flux in potential flow

The momentum is flux (the time derivative of the momentum) is given by

[math]\displaystyle{ \frac{d\overrightarrow{M(t)}}{dt} = \rho \frac{d}{dt} \iiint_{V(t)} \overrightarrow V dV = \rho \iiint_{V(t)} \frac{\partial\overrightarrow{V}}{\partial t} dV + \rho \oint_{S(t)} \overrightarrow{V} U_n dS, }[/math]

where [math]\displaystyle{ U_n \, }[/math] is the outward normal velocity of the surface [math]\displaystyle{ S(t)\, }[/math]. This equation follows from the transport theorem.

We begin with Euler's equation in the absence of viscosity

[math]\displaystyle{ \frac{\partial\overrightarrow{V}}{\partial t} + (\overrightarrow{V} \cdot \nabla ) \overrightarrow V = - \frac{1}{\rho} \nabla P + \overrightarrow g }[/math]

We may recast the rate of change of the momentum ([math]\displaystyle{ \equiv \, }[/math] momentum flux) in the form

[math]\displaystyle{ \frac{d\overrightarrow{M(t)}}{dt} = - \rho \iiint_{V(t)} [ \nabla ( \frac{P}{\rho} + g Z ) + ( \overrightarrow{V} \cdot \nabla ) \overrightarrow{V} ] dV + \rho \oint_{s(t)} \overrightarrow{V} U_n dS }[/math]

So far [math]\displaystyle{ V(t)\, }[/math] is an arbitrary closed time dependent volume bounded by the time dependent surface [math]\displaystyle{ S(t)\, }[/math]. We have however defined the gravitational acceleration to be in the negative [math]\displaystyle{ Z }[/math] direction.

Simplification

We use the following vector theorem

[math]\displaystyle{ (\overrightarrow{V} \cdot \nabla ) \overrightarrow{V} = \nabla ( \frac{1}{2} \overrightarrow{V} \cdot {V} ) - \overrightarrow{V} \times (\nabla \times \overrightarrow{V} ) }[/math]

It we have potential flow then [math]\displaystyle{ \overrightarrow{V} = \nabla \Phi \, }[/math] and we can use Gauss's vector theorem:

[math]\displaystyle{ \iiint_{V(t)} \nabla ( \frac{1}{2} \overrightarrow{V} \cdot \overrightarrow{V} ) dV = \frac{1}{2} \oint_{S(t)} \overrightarrow{V} \cdot \overrightarrow{V} \overrightarrow{n} dS }[/math]

In potential flow it follows that

[math]\displaystyle{ \oint_{S(t)} \frac{1}{2} ( \overrightarrow{V} \cdot \overrightarrow{V} ) \overrightarrow{n} dS = \oint_{S(t)} \frac{\partial\Phi}{\partial n} \nabla \Phi dS = \oint_{S(t)} V_n \overrightarrow{V} dS }[/math]

since for [math]\displaystyle{ \nabla^2 \Phi = 0 \, }[/math];

[math]\displaystyle{ \oint_S \frac{1}{2} ( \nabla\Phi \cdot \nabla\Phi) \overrightarrow{n} dS \equiv \oint_S \frac{\partial\Phi}{\partial n} \nabla\Phi dS. }[/math]

(in the above [math]\displaystyle{ \vec{n} \, }[/math] is the unit vector pointing out of the volume [math]\displaystyle{ V(t) }[/math] [math]\displaystyle{ V_n = \vec{n} \cdot \nabla \Phi }[/math]

Upon substitution inthe momentum flux formula, we obtain:

[math]\displaystyle{ \frac{d\overrightarrow{M}}{dt} = - \rho \oint_S(t) [ ( \frac{P}{\rho} + gZ ) \overrightarrow{n} + \overrightarrow{V} (V_n - U_n )] dS }[/math]

This formula is of central importance in potential flow marine hydrodynamics because the rate of change of the linear momentum defined above is just [math]\displaystyle{ \pm \, }[/math] the force acting on the fluid volume. When its mean value can be shown to vanish, important force expressions on solid boundaries follow and will be derived in what follows.

Hydrostatic Term

Consider separately the term in the momentum flux expression involving the hydrostatic pressure:

[math]\displaystyle{ \frac{d\overrightarrow{M_H}}{dt} = - \rho \oint_S gZ \vec{n}, \ \mbox{where} \ S=S_F + S^{\pm} + S_B + S_{-\infty} }[/math]

The integral over the body surface, assuming a fully submerged body is:

[math]\displaystyle{ \frac{d\overrightarrow{M_{H,B}}}{dt} = - \rho \oint_{S_B} gZ \vec{n} = \rho g V \vec{k} = \overrightarrow{B} }[/math]

where [math]\displaystyle{ V }[/math] is the volume. This follows from the vector theorem of Gauss and is the principle of Archimedes.

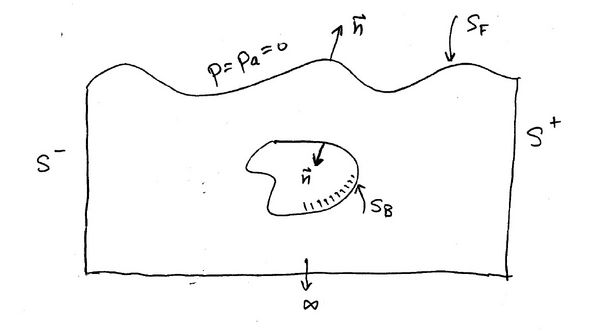
We may therefore consider the second part of the integral involving wave effects independently and in the absence of the body, assumed fully submerged. In the case of a surface piercing body and in the fully nonlinear case matters are more complex. Consider the application of the momentum conservation theorem in the case of a submerged or floating body in steep waves (Figure 1).

Momentum boundaries

Here we consider the two-dimensional case in order to present the concepts. Extensions to three dimensions are then trivial. Note that unlike the energy conservation principle, the momentum conservation theorem derived above is a vector identity with a horizontal and a vertical component. The integral of the hydrostatic term over the remaining surfaces leads to:

[math]\displaystyle{ \frac{d \overrightarrow{M}_{H,S}}{dt} = - \rho \iint_{S_F+S^+ + S^- +S_{\infty}} gZ \bar{n} dS = - \rho g V_{\mbox{Fluid}} \vec{K} }[/math]

where [math]\displaystyle{ V_{\mbox{Fluid}} }[/math] is the fluid volume. This is simply the static weight of the volume of fluid bounded by [math]\displaystyle{ S_F, S^+, S^- \, }[/math] and [math]\displaystyle{ S_{\infty}. }[/math] With no waves present, this is simply the weight of the ocean water "column" bounded by [math]\displaystyle{ S\, }[/math] which does not concern us here. This weight does not change in principle when waves are present at least when [math]\displaystyle{ S^+, S^- \, }[/math] are placed sufficiently far away that the wave amplitude has decreased to zero. So "in principle" this term being of hydrostatic origin may be ignored. However, it is in principle more "rational" to apply the momentum conservation theorem over the "linearized" volume [math]\displaystyle{ V_L(t) \, }[/math] which is perfectly possible within the framework derived above. In this case [math]\displaystyle{ \frac{d\overrightarrow{M}_H}{dt} \, }[/math] is exactly equal to the staic weight of the water column and can be ignored in the wave-body interaction problem. On [math]\displaystyle{ S_F; P=P_a=0 \, }[/math] and hence all terms within the free-surface integral and over [math]\displaystyle{ S_{\infty} \, }[/math] (seafloor) can be neglected. It follows that:

[math]\displaystyle{ \frac{d \overrightarrow{M}}{dt} = - \rho \iint_{S^\pm +S_B} \left[ \frac{P}{\rho} \vec{n} + \overrightarrow{V} (V_n -U_n) \right] dS }[/math]

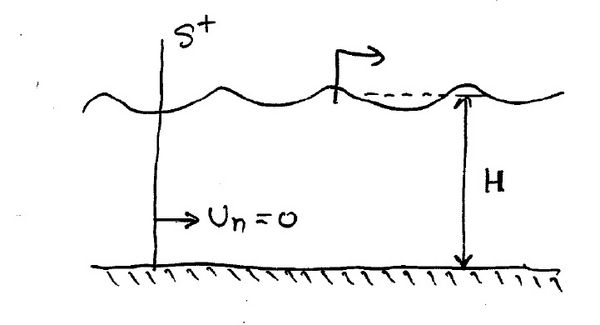
Note that the free surface integrals also vanish for the horizontal component since the hydrostatic force is always vertical. This momentum flux formula is of central importance in wave-body interactions and has many important applications, some of which are discussed bellow. Note that the mathematical derivations involved in its proof apply equally when the volume [math]\displaystyle{ V\, }[/math] and its enclosed surface are selected to be at their linearized positions. In such a case it is essential to set [math]\displaystyle{ U_n=0\, }[/math] and [math]\displaystyle{ V_n \ne 0 }[/math]. Let the math take over and suggest the proper expression for the force. In the fully nonlinear case, [math]\displaystyle{ U_n \ne 0 \, }[/math] on [math]\displaystyle{ S_F\, }[/math] and [math]\displaystyle{ P=0 \, }[/math] on [math]\displaystyle{ S_F \, }[/math]!

On a solid boundary:

[math]\displaystyle{ U_n =V_n \, }[/math]

and

[math]\displaystyle{ \overrightarrow{F}_B = \iint_{S_B} P \vec{n} dS }[/math]

With [math]\displaystyle{ \vec{n} \, }[/math] pointing inside the body. We may therefore recast the momentum conservation theorem in the form:

[math]\displaystyle{ \overrightarrow{F}_B (t) = - \frac{d \overrightarrow{M}}{dt} - \rho \iint_{S^\pm} \left[ \frac{P}{\rho} \vec{n} + \overrightarrow{V} (V_n - U_n) \right] dS }[/math]

Where [math]\displaystyle{ S^\pm \, }[/math] are fluid boundaries at some distance from the body. If the volume of fluid surrounded by the body, free surface and the furfaces [math]\displaystyle{ S^\pm \, }[/math] does not grow in time, then the momentum of the enclosed fluid cannot grow either, so [math]\displaystyle{ \overrightarrow{M}(t) \, }[/math] is a stationary physical quantity. It is a well known result that the mean value in time of the time derivative of a stationary quantity is zero. So:

[math]\displaystyle{ {\overline{\frac{d\overrightarrow{M}}{dt}}}^t = 0 }[/math]

Proof :

[math]\displaystyle{ {\overline{\frac{dF}{dt}}}^t = \lim_{T\to\infty} \frac{1}{2T} \int_{-T}^{T} \frac{dF{\tau}}{d\tau} d\tau = \lim_{T\to\infty} \frac{1}{2T} [F(T) - F(-T) ] }[/math]

Since [math]\displaystyle{ F(\pm \tau) \, }[/math] must be bounded for a stationary signal [math]\displaystyle{ F(t) \, }[/math], it follows that [math]\displaystyle{ {\overline{\frac{dF}{dt}}}^t = 0 \, }[/math].

Taking mean values, it follows that:

[math]\displaystyle{ {\overline{\overrightarrow{F}_B (t)}}^t = - \rho \ {\overline{\iint_{S^\pm} \left[ \frac{P}{\rho} \vec{n} + \overrightarrow{V} (V_n - U_n ) \right] dS}}^t }[/math]

This is the fundamental formula underlying the definition of the mean wave drift forces acting on floating bodies. Such forces are very imprtant for stationary floating structures and can be expressed in terms of integrals of wave effects over control surfaces [math]\displaystyle{ S^\pm \, }[/math] which may be located at infinity.

The extension of the above formula for [math]\displaystyle{ {\overline{\overrightarrow{F}_B}}^t \, }[/math] in three dimensions is trivial. Simply replace [math]\displaystyle{ S^\pm \, }[/math] by [math]\displaystyle{ S_{\infty} \, }[/math], a control surface at infinity. Common choices are a vertical cylindrical boundary or two vertical planes paraller to the axis of forward motion of a ship.

Applications

Mean horizontal momentum flux due to a Plane Progressive Regular Wave

Plane progressive wave momentum

We can determine the mean horizontal momentum flux due to a Plane Progressive Regular Wave with surface displacement

[math]\displaystyle{ \zeta = A \cos (\omega t - K x) \, }[/math]

where [math]\displaystyle{ \omega }[/math] and [math]\displaystyle{ K }[/math] are related by the Dispersion Relation for a Free Surface [math]\displaystyle{ \omega^2 = gK \tanh KH \, }[/math]

The momentum flux across [math]\displaystyle{ S^+ \, }[/math] is given by

[math]\displaystyle{ \frac{dM_X}{dt} = - \int_{-H}^{\zeta} ( P + \rho u^2 ) dZ }[/math]

The pressure is given by Bernoulli's equation

[math]\displaystyle{ P = - \rho \frac{\partial\Phi}{\partial t} - \frac{1}{2} \rho ( u^2 + v^2 ) - \rho g Z }[/math]

so that the momentum flux is

[math]\displaystyle{ \frac{dM_X}{dt} = \rho \int_{-H}^{\zeta} \left[ \frac{\partial\Phi}{\partial t} + \frac{1}{2} ( v^2 - u^2 ) + g Z \right] dZ = \rho \left( \int_{-H}^{0} + \int_{0}^{\zeta} \right) \left[ \frac{\partial\Phi}{\partial t} + \frac{1}{2} (v^2 - u^2) + gZ \right] dZ }[/math]

Taking mean values in time and keeping terms of [math]\displaystyle{ O(A^2) }[/math] we obtain:

[math]\displaystyle{ {\overline{\frac{dM_X}{dt}}}^t = {\overline{\rho \zeta(t) \left. \frac{\partial\Phi}{\partial t} \right |_{H=0}}}^t + \frac{1}{2} \rho \ {\overline{\int_{-H}^{0} (v^2 -u^2 ) dZ}}^t + {\overline{\frac{1}{2} \rho g \zeta^2}}^t }[/math]

Invoking the linearized dynamic free surface condition we obtain

[math]\displaystyle{ \left. \frac{\partial\Phi}{\partial t} \right |_{Z=0} = - g \zeta }[/math]

It follows that:

[math]\displaystyle{ {\overline{\frac{dM_X}{dt}}}^t = {-\frac{1}{2} \rho g \zeta^2 (t)}^t + \frac{1}{2} \rho {\overline{\int_{-H}^0 (v^2-u^2)dZ}}^t }[/math]

In deep water [math]\displaystyle{ \overline{v^2} = \overline{u^2} \, }[/math] and the second term is identically zero, so

[math]\displaystyle{ {\overline{\frac{dM_X}{dt}}}^t = - \frac{1}{2} \rho g {\overline{\zeta^2 (t)}}^t = - \frac{1}{4} \rho g A^2 }[/math]

In water of finite depth the wave particle trajectories are elliptical with the mean horizontal velocities larger than the mean vertical velocities. So:

[math]\displaystyle{ \overline{V_H^2} \lt \overline{U_H^2} }[/math]

Therefore, in finite depth the modulus of the mean momentum flux is higher than in deep water for the same A. So the mean horizontal momentum flux due to a plane progressive wave is against its direction of propagation and equal to [math]\displaystyle{ - \frac{1}{4} \rho g A^2 }[/math].

Wavemaker

Consider a wave maker shown in the figure generating a wave of amplitude [math]\displaystyle{ A }[/math] at infinity.

What is the mean horizontal force on the wavemaker? From the momentum conservation theorem the maan horizontal flux of momentum to the left must flow into the wavemaker. This mean flux translates into a mean horizontal force in the same direction, as shown in the figure. Not an easy conclusion without using some basic fluid mechanics!

Circular object in two dimensions

Two other illustrations of the momentum flux principle are noteworthy: consider a circular object in two dimensions rotating at an angular frequency [math]\displaystyle{ \omega\, }[/math] under a free surface and with a small amplitude. In other words the circle center rotates as a fluid particle in a regular wave.

It can be shown that according to linear theory this rotational motion creates regular waves propagating to the right with no waves propagating to the left! What is the mean horizontal force acting on the circle?

From the momentum conservation principle the mean force [math]\displaystyle{ \overline{F}\, }[/math] acting on the circle must be equal to [math]\displaystyle{ \overline{L} \, }[/math], thus:

[math]\displaystyle{ \overline{F} = - \frac{1}{4} \rho g A^2 }[/math]

.

Dean 1953 has shown that regular plane progressive waves in deep water propagating over a circle fixed under the gree surface are entirely transmitted with a phase shift.

In other words the wave reflection is zero. Note this is the only body in 2 dimensions with this property. Reflection is non-zero in finite depth for all known bodies. Show by applying the momentum conservation principle that the mean horizontal force

[math]\displaystyle{ \overline{F} = 0 }[/math]

Plane progressive waves in general directions.

Free surface elevation:

[math]\displaystyle{ \zeta = A \cos \left( \omega t - K X \cos \beta - K Y \sin \beta \right) }[/math] [math]\displaystyle{ A \mathbf{Re} \left \{ e^{- i K X \cos \beta - i K Y \sin \beta + i \omega t} \right \} }[/math]

Velocity potential in finite depth

[math]\displaystyle{ \Phi = A \mathbf{Re} \left \{ \frac{igA}{\omega} \frac{\cosh K (Z+H)}{\cosh KH} \ e^{ - i K X \cos \beta - i K Y \sin \beta + i \omega t} \right \} }[/math] [math]\displaystyle{ \omega^2 = g K \tanh K H \, }[/math]

Waves reflecting off a vertical wall this is one of the few very important analytical solutions of regular waves interacting with solid boundaries seen in practice. The other is wavemaker theory.

Let the incident wave elevation be:

[math]\displaystyle{ \zeta_I = \mathbf{Re} \left \{ A_I e^{-iKX+i\omega t} \right \} }[/math]

And the reflected be:

[math]\displaystyle{ \zeta_R = \mathbf{Re} \left \{ A_R e^{+iKX+i\omega t} \right \} }[/math]

Where the sign of the [math]\displaystyle{ e^{iKX}\, }[/math] term has been reversed to denote a wave propagating to the left. [math]\displaystyle{ A_R\, }[/math] can be complex in order to allow for phase differences.

The corresponding velocity potentials are:

[math]\displaystyle{ \Phi_I = \mathbf{Re} \left \{ \frac{igA_I}{\omega} \frac{\cosh K (Z+H}{\cosh KH} e^{-iKX+i\omega t} \right \} }[/math] [math]\displaystyle{ \Phi_R = \mathbf{Re} \left \{ \frac{igA_R}{\omega} \frac{\cosh K (Z+H}{\cosh KH} e^{iKX+i\omega t} \right \} }[/math]

On [math]\displaystyle{ X = 0 \, }[/math]:

[math]\displaystyle{ \frac{\partial}{\partial X} \left( \Phi_I + \Phi_R \right) = 0 }[/math]

Or

[math]\displaystyle{ - i K A_I + i K A_R \Longrightarrow A_R = A_I \equiv A }[/math]

The resulting total velocity potential is:

[math]\displaystyle{ \Phi = \Phi_I + \Phi_R = \mathbf{Re} \left \{ \frac{igA_R}{\omega} \frac{\cosh K (Z+H}{\cosh KH} e^{i\omega t} \left( e^{iKX} + e^{-iKX} \right) \right \} }[/math] [math]\displaystyle{ = 2 A \mathbf{Re} \left \{ \frac{ig}{\omega} \frac{\cosh K (Z+H)}{\cosh KH} \cos K X e^{i\omega t} \right \} }[/math]

The resulting standing-wave elevation is:

[math]\displaystyle{ \zeta = \zeta_I + \zeta_R = 2 A \cos K X \cos \omega t \, }[/math]

Exercises

• Apply the momentum conservation principle to determine the mean horizontal force on the break water. Verify your result with the answer from direct pressure integration.

• Derive an expression for the energy density of the standing wave. What is the energy flux?

• Derive expressions for the energy density, energy flux and momentum flux of bi-chromatic waves propagating in the same direction

[math]\displaystyle{ \zeta = A_1 \cos (\omega_1 t - K_1 X) + A_2 \cos ( \omega_2 t - K_2 X ) \, }[/math]

• Repeat the exercise for waves propagating in the opposite directions

[math]\displaystyle{ \zeta = A_1 \cos (\omega_1 t - K_1 X) + A_2 \cos ( \omega_2 t - K_2 X ) \, }[/math]

Assume deep water

• Derive the "standing" wave off a breakwater for a wave incident at an angle [math]\displaystyle{ \beta \, }[/math].

---

This article is based on the MIT open course notes and the original article can be found here

Ocean Wave Interaction with Ships and Offshore Energy Systems