Green Function Methods for Floating Elastic Plates

Introduction

The problem of a two-dimensional Floating Elastic Plate was solved using a Free-Surface Green Function by Newman 1994 and Meylan and Squire 1994. We describe here both methods (which are closely related). A related paper was given by Hermans 2003 and we extended to multiple plates in Hermans 2004.

We present here the solution for a floating elastic plate using dry modes. We begin with the equations. The solution can also be found using Eigenfunction Matching for a Finite Floating Elastic Plate using Symmetry.

Equations for a Finite Plate in Frequency Domain

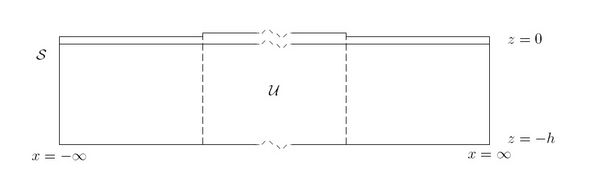
We consider the problem of small-amplitude waves which are incident on finite floating elastic plate occupying water surface for [math]\displaystyle{ -L\lt x\lt L }[/math]. These equations are derived in Floating Elastic Plate The submergence of the plate is considered negligible. We assume that the problem is invariant in the [math]\displaystyle{ y }[/math] direction. We also assume that the plate edges are free to move at each boundary, although other boundary conditions could easily be considered using the methods of solution presented here. We begin with the Frequency Domain Problem for a semi-infinite Floating Elastic Plates in the non-dimensional form of Tayler 1986 (Dispersion Relation for a Floating Elastic Plate). We also assume that the waves are normally incident (incidence at an angle will be discussed later).

[math]\displaystyle{ \Delta \phi = 0, \;\;\; -h \lt z \leq 0, }[/math] [math]\displaystyle{ \partial_z \phi = 0, \;\;\; z = - h, }[/math] [math]\displaystyle{ \partial_z\phi=\alpha\phi, \,\, z=0,\,x\lt -L,\,\,{\rm or}\,\,x\gt L }[/math] [math]\displaystyle{ \partial_x^2\left\{\beta(x) \partial_x^2\partial_z \phi\right\} - \left( \gamma(x)\alpha - 1 \right) \partial_z \phi - \alpha\phi = 0, \;\; z = 0, \;\;\; -L \leq x \leq L, }[/math]

where [math]\displaystyle{ \alpha = \omega^2 }[/math], [math]\displaystyle{ \beta }[/math] and [math]\displaystyle{ \gamma }[/math] are the stiffness and mass constant for the plate respectively. The free edge conditions at the edge of the plate imply

[math]\displaystyle{ \partial_x^3 \partial_z\phi = 0, \;\; z = 0, \;\;\; x = \pm L, }[/math] [math]\displaystyle{ \partial_x^2 \partial_z\phi = 0, \;\; z = 0, \;\;\; x = \pm L, }[/math]

Transformation using Eigenfunctions for a Free Beam

We can find a the eigenfunction which satisfy

[math]\displaystyle{ \partial_x^4 w_n = \lambda_n^4 w_n \,\,\, -L \leq x \leq L }[/math]

plus the edge conditions of zero bending moment and shear stress

[math]\displaystyle{ \begin{matrix} \partial_x^3 w_n= 0 \;\;\;\; \mbox{ at } z = 0 \;\;\; x = \pm L, \end{matrix} }[/math] [math]\displaystyle{ \begin{matrix} \partial_x^2 w_n = 0 \;\;\; \mbox{ at } z = 0 \;\;\; x = \pm L. \end{matrix} }[/math]

This solution is discussed further in Eigenfunctions for a Free Beam.

Expanding

[math]\displaystyle{ \frac{\partial \phi}{\partial z} = i\omega \sum_{n=0}^{\infty} \zeta_n w_n }[/math]

Equation in Terms of the Modes of the Plate

Under these assumptions, the equations become

[math]\displaystyle{ \Delta\phi =0,\,\,-h\lt z\lt 0, }[/math] [math]\displaystyle{ \partial_{z}\phi =0,\,\,z=-h, }[/math] [math]\displaystyle{ \alpha\phi =\partial_{z}\phi,\,\,x\notin(-L,L),\ \ z=0, }[/math] [math]\displaystyle{ i\omega\sum_{n=0}^{\infty}\xi_{n}w_{n} =\partial_{z}\phi,\,\,x\in (-L,L),\,\, z=0, }[/math] [math]\displaystyle{ \sum_{n=0}^{\infty}\alpha_{n}\left( 1+\beta\lambda_{n}^{4}\right) w_{n}-\alpha\gamma\sum_{n=0}^{\infty}\alpha_{n}w_{n} = -i\omega \phi,\,\,x\in(-L,L),\,\, z=0. }[/math]

We solve for the potential (and displacement) as the sum of the diffracted and radiation potentials in the standard way, as for a rigid body. We begin with the diffraction potential [math]\displaystyle{ \phi^{(d)} }[/math] which satisfies the following equations

[math]\displaystyle{ \Delta\phi^{(d)} =0,\,\,-h\lt z\lt 0, }[/math] [math]\displaystyle{ \partial_{z}\phi^{(d)} =0,\,\,z=-h, }[/math] [math]\displaystyle{ \partial_{z}\phi^{(d)} =\alpha \phi^{(d)},\,\,x\notin(-L,L),\,\, z=0, }[/math] [math]\displaystyle{ \partial_{z}\phi^{(d)} =0,\,\,x\in(-L,L),\,\,z=0. }[/math]

Furthermore, [math]\displaystyle{ \phi^{(d)} }[/math] satisfies the Sommerfeld Radiation Condition

[math]\displaystyle{ \frac{\partial}{\partial x} \left(\phi^{(d)}-\phi_{\kappa}^{\rm In} \right) \pm ik\left( \phi^{(d)}-\phi^{\rm In}_{\kappa}\right) = 0 ,\,\,\mathrm{as} \,\,x\rightarrow\pm\infty, }[/math]

where [math]\displaystyle{ k }[/math] is the wavenumber, which is the positive real solution of the Dispersion Relation for a Free Surface

[math]\displaystyle{ k\tanh(kh)=\omega^{2}, }[/math]

and [math]\displaystyle{ \phi^{\rm In} }[/math] is the incident wave given by

[math]\displaystyle{ \phi^{\rm In} = \frac{i\omega}{k\sinh kh} \cosh k(z+h) e^{-i kx} }[/math]

(which has unit amplitude in displacement) and is travelling towards positive infinity

We now consider the radiation potentials [math]\displaystyle{ \phi^{(n)} }[/math], which satisfy the following equations

[math]\displaystyle{ \Delta\phi^{(n)} =0,\,\,-h\lt z\lt 0, }[/math] [math]\displaystyle{ \partial_{z}\phi^{(n)} =0,\,\,z=-h, }[/math] [math]\displaystyle{ \partial_{z}\phi^{(n)} =\alpha\phi^{(n)},\,\,x\notin(-L,L),\, \, z=0 }[/math] [math]\displaystyle{ \partial_{z}\phi^{(n)} = i\omega w_{n},\,\,x\in(-L,L),\,\,z=0. }[/math]

The radiation condition for the radiation potential is

[math]\displaystyle{ \frac{\partial\phi^{(n)}}{\partial x}\pm ik\phi^{(n)}=0,\,\,\mathrm{as} \,\,x\rightarrow\pm\infty. }[/math]

Therefore we find the potential as

[math]\displaystyle{ \phi=\phi^{(s)} +\sum_{n=0}^{\infty}\xi_{n}\phi^{(n)}, }[/math]

so that

[math]\displaystyle{ \sum_{n=0}^{\infty}\left( 1+\beta\lambda_{n}^{4} - \alpha\gamma\right) \xi_{n}w_{n}=-i\omega\phi ^{(s)}_\kappa-i\omega\sum_{n=0}^{\infty}\xi_{n}\phi^{(n)}. }[/math]

If we multiply by [math]\displaystyle{ w_m }[/math] and take an inner product over the plate we obtain

[math]\displaystyle{ \left( 1+\beta\lambda_{n}^{4} - \alpha\gamma\right) \xi_{n}=-i\omega \int_{-b}^{b}\phi^{(s)}_\kappa w_{n}\mathrm{d}x + \sum_{m=0}^{\infty}\left(\omega^2 a_{mn}(\omega) - i\omega b_{mn}(\omega)\right) \xi_{m}, }[/math]

where the functions [math]\displaystyle{ a_{mn}(\omega) }[/math] and [math]\displaystyle{ b_{mn}(\omega) }[/math] are given by

[math]\displaystyle{ \omega^2 a_{mn}(\omega) -i\omega b_{mn}(\omega) = - i\omega\int_{-L}^{L}\phi^{(m)}w_{n}\mathrm{d}x, }[/math]

and they are referred to as the added mass and damping coefficients (see Added-Mass, Damping Coefficients And Exciting Forces for the equivalent definition for a rigid body). respectively. This equation is solved by truncating the number of modes.

Solution for the Radiation and Diffracted Potential

We use the Free-Surface Green Function for two-dimensional waves, with singularity at the water surface since we are only interested in its value at [math]\displaystyle{ z=0. }[/math] Using this we can transform the system of equations to

[math]\displaystyle{ \phi^{(d)}(x) = \phi^{i}(x) + \int_{-L}^{L}G(x,\xi) \alpha\phi^{(d)}(\xi) \mathrm{d} \xi }[/math]

and

[math]\displaystyle{ \phi^{(n)}(x) = \int_{-L}^{L}G(x,\xi) \left( \alpha\phi^{(n)}(\xi) - i\omega w_n(\xi) \right)\mathrm{d} \xi }[/math]

Details about this method can be found in Integral Equation for the Finite Depth Green Function at Surface.

Reflection and Transmission Coefficients

We can calculate the Reflection and Transmission coefficients as follows

A diagram depicting the area [math]\displaystyle{ \Omega }[/math] which is bounded by the rectangle [math]\displaystyle{ \partial\Omega }[/math]. The rectangle [math]\displaystyle{ \partial\Omega }[/math] is bounded by [math]\displaystyle{ -h\leq z \leq0 }[/math] and [math]\displaystyle{ -\infty\leq x \leq \infty }[/math]

Applying Green's theorem to [math]\displaystyle{ \phi }[/math] and [math]\displaystyle{ \phi^{i} }[/math] gives

[math]\displaystyle{ 0 = \iint_{\Omega}(\phi\nabla^2\phi^{i} - \phi^{i}\nabla^2\phi)\mathrm{d}x\mathrm{d}z = \int_{\partial\Omega}(\phi\frac{\partial\phi^*}{\partial n} - \phi^*\frac{\partial\phi}{\partial n})\mathrm{d}l, }[/math] [math]\displaystyle{ = \int_{-L}^{L} e^{k_0 x} \left(\alpha \phi(x) - \partial_n \phi(x)\right)\mathrm{d}x - k_0 R \int_{-h}^{0} \left(\phi_0(z)\right)^2 \mathrm{d}z. }[/math]

Therefore

[math]\displaystyle{ R = k_0 \frac{\int_{-L}^{L} e^{k_0 x} \left(\alpha \phi(x) - \partial_n \phi(x)\right)\mathrm{d}x } {\int_{-h}^{0} \left(\phi_0(z)\right)^2 \mathrm{d}z}. }[/math]

and using a wave incident from the right we obtain

[math]\displaystyle{ 1 + T = k_0 \frac{\int_{-L}^{L} e^{-k_0 x} \left(\alpha \phi(x) - \partial_n \phi(x)\right)\mathrm{d}x } {\int_{-h}^{0} \left(\phi_0(z)\right)^2 \mathrm{d}z}. }[/math]

Matlab Code

A program to calculate the solution in elastic modes can be found here A program to calculate the solution in elastic modes can be found here

elastic_plate_modes.m

Additional code

This program requires

• matrix_G_surface.m
• two_d_finite_depth_Green_surface.m
• dispersion_free_surface.m
• beam_ev.m
• beam_em.m

Additional code

This program requires

• matrix_G_surface.m
• dispersion_free_surface.m

Alternative Solution Method using Green Function for the Plate

We can also solve the equation by a closely related method which was given in Meylan and Squire 1994. We can transform the equations to

[math]\displaystyle{ \phi(x) = \phi^{\rm In}(x) + \int_{-L}^{L}G(x,\xi) \left( \alpha\phi(\xi) - \partial_z\phi(\xi) \right)\mathrm{d} \xi }[/math]

Expanding as before

[math]\displaystyle{ \partial_z \phi = i\omega \sum \xi_n w_n }[/math]

we obtain

[math]\displaystyle{ -i\omega \phi = \sum \left(\beta\lambda_n^4 - \gamma\alpha + 1\right)\xi_n w_n }[/math]

This leads to the following equation

[math]\displaystyle{ \partial_z\phi(x) = \frac{1}{\alpha} \int_{-L}^{L} \frac{w_n(x)w_n(\xi)}{\beta\lambda_n^4 - \gamma\alpha + 1} \phi(\xi)\mathrm{d}\xi }[/math]

or

[math]\displaystyle{ \partial_z\phi(x) = \frac{1}{\alpha} \int_{-L}^{L} g(x,\xi) \phi(\xi)\mathrm{d}\xi }[/math]

where

[math]\displaystyle{ g(x,\xi) = \frac{w_n(x)w_n(\xi)}{\beta\lambda_n^4 - \gamma\alpha + 1} }[/math]

which is the Green function for the plate.