Introduction
We derive here a condition which must be satisfied for energy balance for two semi-infinite elastic plates. The solution applies
to the problem of multiple elastic plates and from here we know we can write the potential as
[math]\displaystyle{
\phi \approx \left\{
\begin{matrix}
{
Ie^{\kappa_{1}(0)(x-r_1)}\frac{\cos(k_1(0)(z+h))}{\cos(k_1(0)h)} }+\\
{
\qquad \qquad \sum_{n=-2}^{M}R_1(n) e^{\kappa_{1}(n)(x-r_1)} \frac{\cos(k_1(n)(z+h))}{\cos(k_1(n)h)} },&
\mbox{ for } x \lt r_1,\\
{
\sum_{n=-2}^{M}T_{\mu}(n) e^{-\kappa_\mu(n)(x-l_\mu)}
\frac{\cos(k_\mu(n)(z+h))}{\cos(k_\mu(n)h)} } + \\
{
\qquad \qquad \sum_{n=-2}^{M}R_{\mu}(n) e^{\kappa_\mu(n)(x-r_\mu)}
\frac{\cos(k_\mu(n)(z+h))}{\cos(k_\mu(n)h)} },
&\mbox{ for } l_\mu\lt x \lt r_\mu,\\
{
\sum_{n=-2}^{M}T_{\Lambda}(n)e^{-\kappa_{\Lambda}(n)(x-l_\Lambda)}
\frac{\cos(k_\Lambda(n)(z+h))}{\cos(k_\Lambda(n)h)} }, &\mbox{ for } l_\Lambda\lt x,
\end{matrix} \right.
}[/math]
(for details of this notation see Eigenfunction Matching Method for Floating Elastic Plates).
Equations
Based on the method used in Evans and Davies 1968, a check can be made to ensure the solutions of the floating plate problem are in energy balance.
This is simply a condition that the incident energy is equal to the sum of the radiated energy.
When the first and final plates have different properties, the energy balance equation is derived by applying Green's theorem to [math]\displaystyle{ \phi }[/math] and its conjugate.
The domain of integration is shown in the figure on the right.
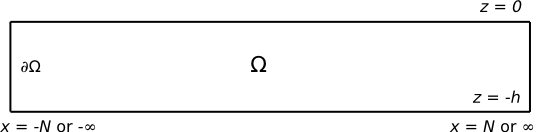
A diagram depicting the area
[math]\displaystyle{ \Omega }[/math] which is bounded by the rectangle
[math]\displaystyle{ \partial\Omega }[/math].The rectangle
[math]\displaystyle{ \partial\Omega }[/math] is bounded by
[math]\displaystyle{ -h\leq z \leq0 }[/math] and
[math]\displaystyle{ -\infty/-N\leq x \leq N/\infty }[/math]Applying Green's theorem to [math]\displaystyle{ \phi }[/math] and its conjugate [math]\displaystyle{ \phi^* }[/math] gives
[math]\displaystyle{
{ \iint_{\Omega}(\phi\nabla^2\phi^* - \phi^*\nabla^2\phi)\mathrm{d}x\mathrm{d}z
= \int_{\partial\Omega}(\phi\frac{\partial\phi^*}{\partial n} - \phi^*\frac{\partial\phi}{\partial n})\mathrm{d}l },
}[/math]
where [math]\displaystyle{ n }[/math] denotes the outward plane normal to the boundary and [math]\displaystyle{ l }[/math] denotes the plane parallel to the boundary.
As [math]\displaystyle{ \phi }[/math] and [math]\displaystyle{ \phi^* }[/math] satisfy the Laplace's equation, the left hand side of the Green theorem equation vanishes so that it reduces to
[math]\displaystyle{
\Im\int_{\partial\Omega}\phi\frac{\partial\phi^*}{\partial n} \mathrm{d}l = 0,
}[/math]
Expanding gives
[math]\displaystyle{
\xi_1 +\xi_2 + \xi_3 = 0,
}[/math]
where
[math]\displaystyle{
\xi_1 =
-{ \Im\int_{-h}^0(\phi\frac{\partial\phi^*}{\partial x})\big|_{x=-\infty}\mathrm{d}z },
}[/math]
[math]\displaystyle{
\xi_2 =
{ \Im\int_{-h}^0(\phi\frac{\partial\phi^*}{\partial x})\big|_{x=\infty}\mathrm{d}z },
}[/math]
and
[math]\displaystyle{
\xi_3 =
{ \Im\int_{-\infty}^{\infty}(\phi\frac{\partial\phi^*}{\partial z})\big|_{z=0}\mathrm{d}x } ,
}[/math]
where [math]\displaystyle{ \Im }[/math] denotes the imaginary part. The bottom domain composant is obviously equal to zero because of the no-influx condition over the seabed ([math]\displaystyle{ \frac{\partial\phi^*}{\partial z}\big|_{z=-h}=0 }[/math]).
Expanding [math]\displaystyle{ \mathbf{\xi_1} }[/math]
Near [math]\displaystyle{ x=-\infty }[/math], we approximate [math]\displaystyle{ \phi }[/math] by
[math]\displaystyle{
\phi \approx e^{-\kappa_{1}(0)(x-r_1)}\frac{\cos{(k_1(0)(z+h))}}{\cos{(k_1(0)h)}} +
R_1(0)e^{\kappa_{1}(0)(x-r_1)}\frac{\cos{(k_{1}(0)(z+h))}}{\cos{(k_{1}(0)h)}}
}[/math]
Therefore,
[math]\displaystyle{
\begin{matrix}
\xi_1 & = & {-\Im\int_{-h}^0 \left[\left(e^{-i\kappa^{I}_1(x)}+ R_1(0)e^{i\kappa^{I}_1(x)}\right)\right.}
{ \left(i\kappa^{I}_1e^{i\kappa^{I}_1(x)} - i\kappa^{I}_1R_1(0)^*e^{-i\kappa^{I}_1(x)}\right) }
{ \left.\left(\frac{\cosh^2{(k^I_1(z+h))}}{\cosh^2{(k^I_1h)}}\right)\right]\mathrm{d}z, }\\ \\
& = & { - \Im\left[\frac{i\kappa^{I}_1\left(1 - |R_1(0)|^2\right)}{2\cosh^2{(k^I_1h)}}
\int_{-h}^0 \left(\cosh{(2k^I_1(z+h))+1}\right)\mathrm{d}z\right] ,}\\ \\
& = & { - \Im\left[\frac{i\kappa^{I}_1\left(1 - |R_1(0)|^2\right)}{2\cosh^2{(k^I_1h)}}
\left[\frac{1}{2k^I_1}\sinh{(2k^I_1(z+h))} + z\right]_{-h}^0\right], }\\ \\
& = & { - \frac{\kappa^{I}_1\left(1 - |R_1(0)|^2\right)}{2\cosh^2{(k^I_1h)}} \left(\frac{1}{2k^I_1}\sinh{(2k^I_1h))} + h\right) ,}\\ \\
& = & { - \frac{\kappa^{I}_1\left(1 - |R_1(0)|^2\right)}{2k^I_1}\left(\tanh{(k^I_1h)}+\frac{hk^I_1}{\cosh^2{(k^I_1h)}}\right) , }
\end{matrix}
}[/math]
where [math]\displaystyle{ R_1(0)^* }[/math] is the conjugate of [math]\displaystyle{ R_1(0) }[/math].
Expanding [math]\displaystyle{ \mathbf{\xi_2} }[/math]
Near [math]\displaystyle{ x=\infty }[/math], we approximate [math]\displaystyle{ \phi }[/math] by
[math]\displaystyle{
\begin{matrix}
{ \phi \approx T_\Lambda(0)e^{-\kappa_{\Lambda}(0)(x)}\frac{\cos{(k_\Lambda(0)(z+h))}}{\cos{(k_\Lambda(0)h)}}, }
\end{matrix}
}[/math]
and re-express as
[math]\displaystyle{
\phi \approx T_\Lambda(0)e^{-i\kappa^I_\Lambda(x)}\frac{\cosh{(k^I_\Lambda(z+h))}}{\cosh{(k^I_\Lambda h)}},
}[/math]
where [math]\displaystyle{ k^I_\Lambda = \Im k_{\Lambda}(0) }[/math] and [math]\displaystyle{ \kappa^I_\Lambda=\Im \kappa_\Lambda(0) }[/math], so that
[math]\displaystyle{
\frac{\partial\phi}{\partial x} \approx -i\kappa^I_{\Lambda}T_\Lambda(0)e^{-i\kappa^I_{\Lambda}(x)}\frac{\cosh{(k^I_\Lambda(z+h))}}{\cosh{(k^I_\Lambda h)}}.
}[/math]
We know that [math]\displaystyle{ \kappa_\Lambda(0)=\sqrt{k_{\Lambda}(0)^2-(ik_y)^2} }[/math], where [math]\displaystyle{ k_y }[/math] is real and depends on the incident angle [math]\displaystyle{ \theta }[/math]. When [math]\displaystyle{ \theta }[/math] becomes greater than a certain angle [math]\displaystyle{ \theta_0 }[/math] defined by [math]\displaystyle{ \sin \theta_0=\frac{k_{\Lambda}(0)}{k_{1}(0)} }[/math], [math]\displaystyle{ \kappa_\Lambda(0) }[/math] becomes real so the potential becomes real as well. Thus the imaginary part is equal to 0. In that case, we have [math]\displaystyle{ \xi_2=0 }[/math].
Therefore, if [math]\displaystyle{ \theta \in [-\theta_0, \theta_0] }[/math],
[math]\displaystyle{
\begin{matrix}
\xi_2 & = & \Im\int_{-h}^0 \left[\right.(T_\Lambda(0)e^{-i\kappa^I_{\Lambda}(x)})(i\kappa^I_{\Lambda}T_\Lambda(0)^*e^{i\kappa^I_{\Lambda}(x)})
\frac{\cosh^2{(k^I_\Lambda(z+h))}}{\cosh^2{(k^I_\Lambda h)}}\left.\right]dz, \\ \\
& = & { \frac{\kappa^I_{\Lambda}|T_\Lambda(0)|^2}{2\cosh^2{(k^I_\Lambda h)}}
\left(\frac{1}{2k^I_\Lambda}\sinh{(2k^I_\Lambda h)} + h\right)},\\ \\
& = & { \frac{\kappa^I_{\Lambda}|T_\Lambda(0)|^2}{2k^I_\Lambda}\left(\tanh{(k^I_\Lambda h)}+\frac{k^I_\Lambda h}{\cosh^2{(k^I_\Lambda h)}}\right)},
\end{matrix}
}[/math]
otherwise [math]\displaystyle{ \xi_2=0 }[/math].
Expanding [math]\displaystyle{ \mathbf{\xi_3} }[/math]
The ice-covered boundary condition for the Floating Elastic Plate gives
[math]\displaystyle{
\xi_3 = { \Im\int_{-\infty}^{\infty}\left(\frac{\beta}{\alpha}
\left(\frac{\partial^2}{\partial x^2} - k_y^2\right)^2 - \gamma + \frac{1}{\alpha}\right)
\frac{\partial\phi}{\partial z}\cdot\frac{\partial\phi^*}{\partial z}\bigg|_{z=0}dx.}
}[/math]
Since [math]\displaystyle{ {\frac{\partial\phi}{\partial z}\cdot\frac{\partial\phi^*}{\partial z}} }[/math] is real,
[math]\displaystyle{
\xi_3 = \Im\int_{-\infty}^{\infty}\left(\frac{\beta}{\alpha}\frac{\partial^2}{\partial x^2}
\left(\frac{\partial^2}{\partial x^2} - 2k_y^2\right) \right)
\frac{\partial\phi}{\partial z}\cdot\frac{\partial\phi^*}{\partial z}\bigg|_{z=0}dx.
}[/math]
Integration by parts gives
[math]\displaystyle{
\xi_3 = \Im\left\{\left[\frac{\beta}{\alpha}\frac{\partial}{\partial x}
\left(\frac{\partial^2}{\partial x^2}-2k_y^2\right)
\frac{\partial\phi}{\partial z}\cdot\frac{\partial\phi^*}{\partial z}\right]_{-\infty}^{\infty}
-\int_{-\infty}^{\infty}\frac{\beta}{\alpha}\frac{\partial}{\partial x}
\left(\frac{\partial^2}{\partial x^2} - 2k_y^2\right)
\frac{\partial\phi}{\partial z}\cdot\frac
{\partial}{\partial x}\frac{\partial\phi^*}{\partial z}dx
\right\}.
}[/math]
As [math]\displaystyle{ {2k_y^2\frac{\partial}{\partial x}\frac{\partial\phi}{\partial z}\cdot \frac{\partial}{\partial x}\frac{\partial\phi^*}{\partial z}} }[/math] is real and by integration by parts, the expression of [math]\displaystyle{ \xi_3 }[/math] becomes,
[math]\displaystyle{
\xi_3 =\Im\left\{
\left[\frac{\beta}{\alpha}\frac{\partial}{\partial x}
\left(\frac{\partial^2}{\partial x^2}-2k_y^2\right)
\frac{\partial\phi}{\partial z}\cdot\frac{\partial\phi^*}{\partial z}\right]_{-\infty}^{\infty}
- \left[\frac{\beta}{\alpha}\frac{\partial^2}{\partial x^2}\frac{\partial\phi}{\partial z}\cdot
\frac{\partial}{\partial x}\frac{\partial\phi^*}{\partial z}\right]_{-\infty}^{\infty}
+ \int_{-\infty}^\infty\frac{\beta}{\alpha}\frac{\partial^2}{\partial x^2}\frac{\partial\phi}{\partial z}\cdot
\frac{\partial^2}{\partial x^2}\frac{\partial\phi^*}{\partial z}dx\right\}.
}[/math]
As [math]\displaystyle{ {\frac{\partial^2}{\partial x^2}\frac{\partial\phi}{\partial z}\cdot \frac{\partial^2}{\partial x^2}\frac{\partial\phi^*}{\partial z}} }[/math] is real, we obtain the new expression of [math]\displaystyle{ \xi_3 }[/math]
[math]\displaystyle{
\xi_3 = \Im\left\{
\left[\frac{\beta}{\alpha}\frac{\partial}{\partial x}
\left(\frac{\partial^2}{\partial x^2}-2k_y^2\right)
\frac{\partial\phi}{\partial z}\cdot\frac{\partial\phi^*}{\partial z}\right]_{-\infty}^{\infty}-
\left[\frac{\beta}{\alpha}\frac{\partial^2}{\partial x^2}\frac{\partial\phi}{\partial z}\cdot
\frac{\partial}{\partial x}\frac{\partial\phi^*}{\partial z}\right]_{-\infty}^{\infty}\right\}.
}[/math]
Now breaking [math]\displaystyle{ \xi_3 }[/math] down, we can simplify the left hand term for [math]\displaystyle{ x\gt 0 }[/math],
if [math]\displaystyle{ \theta \in [-\theta_0, \theta_0] }[/math],
[math]\displaystyle{
\begin{matrix}
\frac{\partial}{\partial x}\left(\frac{\partial^2}{\partial x^2}-2k_y^2\right)
\frac{\partial\phi(x_2,0)}{\partial z}\cdot\frac{\partial\phi(x_2,0)^*}{\partial z} \\ \\
= \left((-i\kappa^I_{\Lambda})^3k^I_\Lambda T_\Lambda(0)e^{-i\kappa^I_{\Lambda}(x)}\tanh{(k^I_\Lambda h)}\right.
\left.- 2k_y^2(-i\kappa_{\Lambda}(0))k^I_\Lambda T_\Lambda(0)e^{-i\kappa^I_{\Lambda}(x)} \tanh{(k^I_\Lambda h)}\right)
\left(k^I_\Lambda T_\Lambda(0)^*e^{i\kappa^I_{\Lambda}(x)}\tanh{(k^I_\Lambda h)}\right), \\ \\
= i\kappa^I_{\Lambda} (k^I_\Lambda)^2\left((\kappa^I_{\Lambda})^2 + 2k_y^2 \right) \tanh^2{(k^I_\Lambda h)}|T_\Lambda(0)|^2,
\end{matrix}
}[/math]
else this term is equal to 0.
and for [math]\displaystyle{ x\lt 0 }[/math]
[math]\displaystyle{
\begin{matrix}
\frac{\partial}{\partial x}\left(\frac{\partial^2}{\partial x^2}-2k_y^2\right)\frac{\partial\phi(x_1,0)}{\partial z}\cdot
\frac{\partial\phi(x_1,0)^*}{\partial z} \\ \\
= \left[i(\kappa^I_{1})^3k^I_1\left(e^{-i\kappa^I_{1}(x)}-R_1(0)e^{i\kappa^I_{1}(x)}\right) \tanh{(k^I_1 h)}
- 2ik_y^2\kappa^I_{1}k^I_1\left(-e^{-i\kappa^I_{1}(x)} + R_1(0)e^{i\kappa^I_{1}(x)}\right) \tanh{(k^I_1h)}\right]
\left[k^I_1\left(e^{i\kappa^I_{1}(x)} + R_1(0)^*e^{-i\kappa^I_{1}(x))}\right) \tanh{(k^I_1h)}\right], \\ \\
= \left[i\kappa^I_{1}k_1(0)((\kappa^I_{1})^2 + 2k_y^2)\left(e^{-i\kappa^I_{1}(x)} - R_1(0)e^{i\kappa^I_{1}(x)}\right)
\tanh{(k^I_1h)}\right]
\left[k^I_1\left(e^{i\kappa^I_{1}(x)} + R_1(0)^*e^{-i\kappa^I_{1}(x))}\right) \tanh{(k^I_1h)}\right], \\ \\
= i\kappa^I_{1}(k^I_1)^2\left((\kappa^I_{1})^2 + 2k_y^2\right)\tanh^2{(k^I_1h)}\left(1 - |R_1(0)|^2\right),
\end{matrix}
}[/math]
Likewise we expand the right hand term for [math]\displaystyle{ x\gt 0 }[/math], if [math]\displaystyle{ \theta \in [-\theta_0, \theta_0] }[/math],
[math]\displaystyle{
\begin{matrix}
\frac{\partial^2}{\partial x^2}\frac{\partial\phi(x_2,0)}{\partial z}\cdot
\frac{\partial}{\partial x}\frac{\partial\phi^*}{\partial z} \\ \\
= \left[-(\kappa^I_{\Lambda})^2k^I_\Lambda T_\Lambda(0)e^{-i\kappa^I_{\Lambda}(x)} \tanh{(k^I_\Lambda h)}\right]
\left[i\kappa^I_{\Lambda} k^I_\Lambda T_\Lambda(0)^*e^{i\kappa^I_{\Lambda}(x)} \tanh{(k^I_\Lambda h)}\right], \\ \\
= -i(\kappa^I_{\Lambda})^3(k^I_\Lambda)^2\tanh^2{(k^I_\Lambda h)}|T_\Lambda(0)|^2,
\end{matrix}
}[/math]
else this term is equal to 0 as well,
and finally for [math]\displaystyle{ x\lt 0 }[/math],
[math]\displaystyle{
\begin{matrix}
\frac{\partial^2}{\partial x^1}\frac{\partial\phi(x_1,0)}{\partial z}\cdot
\frac{\partial}{\partial x}\frac{\partial\phi^*}{\partial z}\\ \\
= \left[-(\kappa^I_{1})^2k^I_1\left(e^{-i\kappa^I_{1}(x)} + R_1(0)e^{i\kappa^I_{1}(x)}\right)\tanh{(k^I_1 h)}\right]
\left[i\kappa^I_{1} k^I_1\left(e^{i\kappa^I_{1}(x)} - R_1(0)e^{-i\kappa^I_{1}(x)}\right)\tanh{(k^I_1 h)}\right], \\ \\
= -i(\kappa^I_{1})^3(k^I_1)^2\tanh^2{(k^I_1h)}\left(1 - |R_1(0)|^2\right).
\end{matrix}
}[/math]
We can now express [math]\displaystyle{ \xi_3 }[/math] as
[math]\displaystyle{
\begin{matrix}
\xi_3 & = & \Im
\left\{\frac{\beta_\Lambda}{\alpha}\left[i\kappa^I_{\Lambda} (k^I_\Lambda)^2\left((\kappa^I_{\Lambda})^2 + 2k_y^2 \right)
\tanh^2{(k^I_\Lambda h)}|T_\Lambda(0)|^2\right]
-\frac{\beta_1}{\alpha}\left[i\kappa^I_{1}(k^I_1)^2\left((\kappa^I_{1})^2 + 2k_y^2\right)\tanh^2{(k^I_1h)}
\left(1 - |R_1(0)|^2\right)\right]
-\frac{\beta_\Lambda}{\alpha}\left[-i(\kappa^I_{\Lambda})^3(k^I_\Lambda)^2\tanh^2{(k^I_\Lambda h)}|T_\Lambda(0)|^2\right]
+\frac{\beta_1}{\alpha}\left[-i(\kappa^I_{1})^3(k^I_1)^2\tanh^2{(k^I_1h)} \left(1 - |R_1(0)|^2\right)\right]\right\}, \\ \\
& = & \frac{\beta_\Lambda}{\alpha}\left[2\kappa^I_{\Lambda} (k^I_\Lambda)^2((\kappa^I_{\Lambda})^2 + k_y^2)\tanh^2{(k^I_\Lambda h)}|T_\Lambda(0)|^2\right]
-\frac{\beta_1}{\alpha}\left[2\kappa^I_{1}(k^I_1)^2((\kappa^I_{1})^2 + k_y^2)\tanh^2{(k^I_1h)}(1-|R_1(0)|^2)\right].
\end{matrix}
}[/math]
if [math]\displaystyle{ \theta \in [-\theta_0, \theta_0] }[/math], and if not, we obtain:
[math]\displaystyle{
\xi_3 = -\frac{\beta_1}{\alpha}\left[2\kappa^I_{1}(k^I_1)^2((\kappa^I_{1})^2 + k_y^2)\tanh^2{(k^I_1h)}(1-|R_1(0)|^2)\right].
}[/math]
Solving the Energy Balance Equation
Pulling it all together for the case [math]\displaystyle{ \theta \in [-\theta_0, \theta_0] }[/math], we finally obtain
[math]\displaystyle{
\frac{\beta_\Lambda}{\alpha}\left[2\kappa^I_{\Lambda}(k^I_\Lambda)^2((\kappa^I_{\Lambda})^2 +k_y^2)
\tanh^2{(k^I_\Lambda h)}|T_\Lambda(0)|^2\right]
-\frac{\beta_1}{\alpha}\left[2\kappa^I_{1}(k^I_1)^2((\kappa^I_{1})^2 +k_y^2)\tanh^2{(k^I_1h)}(1-|R_1(0)|^2)\right]
+ \frac{\kappa^I_{\Lambda}|T_\Lambda(0)|^2}{2k^I_\Lambda}\left(\tanh{(k^I_\Lambda h)}+
\frac{k^I_\Lambda h}{\cosh^2{(k^I_\Lambda h)}}\right)
- \frac{\kappa^I_{1}\left(1 - |R_1(0)|^2\right)}{2k^I_1}\left(\tanh{(k^I_1h)}+\frac{hk^I_1}{\cosh^2{(k^I_1h)}}\right)=0.
}[/math]
Re-arranging gives
[math]\displaystyle{
\kappa^I_{\Lambda}\tanh{(k^I_\Lambda h)}
\left(\frac{\beta_\Lambda}{\alpha}2(k^I_\Lambda)^2((\kappa^I_{\Lambda})^2 +k_y^2)\tanh{(k^I_\Lambda h)}
+ \frac{1}{2k^I_\Lambda}+\frac{h}{2\sinh{(k^I_\Lambda h)}\cosh{(k^I_\Lambda h)}}\right)|T_\Lambda(0)|^2
\quad - \kappa^I_{1}\tanh{(k^I_1 h)}
\left(\frac{\beta_1}{\alpha}2(k^I_1)^2((\kappa^I_{1})^2 +k_y^2)\tanh{(k^I_1 h)}
+ \frac{1}{2it}+\frac{h}{2\sinh{(k^I_1 h)}\cosh{(k^I_1 h)}}\right)(1-|R_1(0)|^2)=0
}[/math]
which can be expressed as
[math]\displaystyle{
D |T_{\Lambda}(0)|^2 + |R_{1}(0)|^2 = 1,
}[/math]
where [math]\displaystyle{ D }[/math] is given by
[math]\displaystyle{
D = \left(\frac{\kappa^I_{\Lambda} k^I_1\cosh^2{(k^I_1h)}}{\kappa^I_{1}k^I_\Lambda\cosh^2{(k^I_\Lambda h)}}\right)
\left(\frac{-\frac{\beta_\Lambda}{\alpha}4(k^I_\Lambda)^5\sinh^2{(k^I_\Lambda h)} +
\frac{1}{2}{\sinh{(2k^I_\Lambda h)}}+k^I_\Lambda h}
{-\frac{\beta_1}{\alpha}4(k^I_1)^5\sinh^2{(k^I_1h)} +
\frac{1}{2}{\sinh{(2k^I_1h)}}+k^I_1h}\right)
}[/math]
For the case of greater angles, there are no terms depending on [math]\displaystyle{ |T_{\Lambda}(0)|^2 }[/math], so we obtain [math]\displaystyle{ D=0 }[/math] and [math]\displaystyle{ |R_{1}(0)|^2 = 1 }[/math], which is the case of the total reflexion. No energy is transmitted in the [math]\displaystyle{ x\gt 0 }[/math] region.
