Template:Derivation of reflection and transmission in two dimensions

The Reflection and Transmission Coefficients represent the ratio of the amplitude of the reflected or transmitted wave to the amplitude of the incident wave. Conservation of energy means that [math]\displaystyle{ |R|^2+|T|^2=1\, }[/math].

A diagram depicting the area [math]\displaystyle{ \Omega\, }[/math] which is bounded by the rectangle [math]\displaystyle{ \partial \Omega \, }[/math]. The rectangle [math]\displaystyle{ \partial \Omega \, }[/math] is bounded by [math]\displaystyle{ -h \leq z \leq 0 \, }[/math] and [math]\displaystyle{ -\infty \leq x \leq \infty \, }[/math] or [math]\displaystyle{ -N \leq x \leq N\, }[/math]

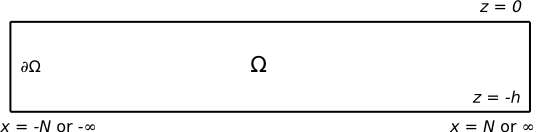
We can calculate the Reflection and Transmission coefficients by applying Green's theorem to [math]\displaystyle{ \phi\, }[/math] and [math]\displaystyle{ \phi^{\mathrm{I}}\, }[/math] [math]\displaystyle{ \phi^{\mathrm{I}}\, }[/math] is a plane wave travelling in the [math]\displaystyle{ x }[/math] direction,

[math]\displaystyle{ \phi^{\mathrm{I}}(x,z)=A \phi_0(z) e^{\mathrm{i} k x} \, }[/math]

where [math]\displaystyle{ A }[/math] is the wave amplitude (in potential) [math]\displaystyle{ \mathrm{i} k }[/math] is the positive imaginary solution of the Dispersion Relation for a Free Surface (note we are assuming that the time dependence is of the form [math]\displaystyle{ \exp(-\mathrm{i}\omega t) }[/math]) and

[math]\displaystyle{ \phi_0(z) =\frac{\cosh k(z+h)}{\cosh k h} }[/math]

We assume that [math]\displaystyle{ A=1 }[/math]. This gives us

[math]\displaystyle{ \iint_{\Omega}(\phi\nabla^2\phi^{\mathrm{I}} - \phi^{\mathrm{I}}\nabla^2\phi)\mathrm{d}x\mathrm{d}z = \int_{\partial\Omega}(\phi\frac{\partial\phi^{\rm I}}{\partial n} - \phi^{\rm I}\frac{\partial\phi}{\partial n})\mathrm{d}l = 0, }[/math] [math]\displaystyle{ = \phi_0(0) \int_{-L}^{L} e^{k_0 x} \left(\alpha \phi(x) - \partial_n \phi(x)\right)\mathrm{d}x - 2k_0 R \int_{-h}^{0} \left(\phi_0(z)\right)^2 \mathrm{d}z. }[/math]

<br\>

where [math]\displaystyle{ k_0 \, }[/math] is the first imaginery root of the dispersion equation and the incident wave is of the form: [math]\displaystyle{ \phi^I=\phi_0(z)e^{-ikx} \, }[/math] Therefore, in the case of a floating plate (where z=0):

[math]\displaystyle{ R = \frac{\int_{-L}^{L} e^{k_0 x} \left(\alpha \phi(x) - \partial_n \phi(x)\right)\mathrm{d}x } {2 k_0 \int_{-h}^{0} \left(\phi_0(z)\right)^2 \mathrm{d}z}. }[/math]

and using a wave incident from the right we obtain

[math]\displaystyle{ 1 + T = \frac{\int_{-L}^{L} e^{-k_0 x} \left(\alpha \phi(x) - \partial_n \phi(x)\right)\mathrm{d}x } {2 k_0 \int_{-h}^{0} \left(\phi_0(z)\right)^2 \mathrm{d}z}. }[/math]