The Reflection and Transmission Coefficients represent the ratio of the amplitude of the reflected or transmitted wave to the amplitude of the incident wave. Conservation of energy means that [math]\displaystyle{ |R|^2+|T|^2=1\, }[/math].
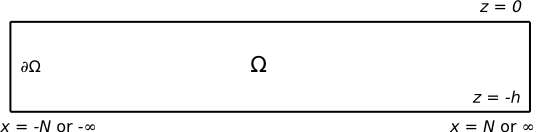
A diagram depicting the area
[math]\displaystyle{ \Omega\, }[/math] which is bounded by the rectangle
[math]\displaystyle{ \partial \Omega \, }[/math]. The rectangle
[math]\displaystyle{ \partial \Omega \, }[/math] is bounded by
[math]\displaystyle{ -h \leq z \leq 0 \, }[/math] and
[math]\displaystyle{ -\infty \leq x \leq \infty \, }[/math] or
[math]\displaystyle{ -N \leq x \leq N\, }[/math]We can calculate the Reflection and Transmission coefficients by
applying Green's theorem to [math]\displaystyle{ \phi\, }[/math] and [math]\displaystyle{ \phi^{\mathrm{I}}\, }[/math]
[math]\displaystyle{ \phi^{\mathrm{I}}\, }[/math]
is a plane wave travelling in the [math]\displaystyle{ x }[/math] direction,
[math]\displaystyle{
\phi^{\mathrm{I}}(x,z)=A \phi_0(z) e^{\mathrm{i} k x} \,
}[/math]
where [math]\displaystyle{ A }[/math] is the wave amplitude (in potential) [math]\displaystyle{ \mathrm{i} k }[/math] is
the positive imaginary solution of the Dispersion Relation for a Free Surface
(note we are assuming that the time dependence is of the form [math]\displaystyle{ \exp(-\mathrm{i}\omega t) }[/math])
and
[math]\displaystyle{
\phi_0(z) =\frac{\cosh k(z+h)}{\cosh k h}
}[/math]
We assume that [math]\displaystyle{ A=1 }[/math]. This gives us
[math]\displaystyle{
\iint_{\Omega}(\phi\Delta\phi^{\mathrm{I}} - \phi^{\mathrm{I}}\Delta\phi)\mathrm{d}x\mathrm{d}z
= \int_{\partial\Omega}(\phi \partial_n \phi^{\rm I} - \phi^{\rm I}\partial_n\phi)\mathrm{d}l = 0,
}[/math]
This means that (using the far field behaviour of the potential [math]\displaystyle{ \phi }[/math])
[math]\displaystyle{
\int_{\partial\Omega_{B}}
(\phi \partial_n \phi^{\rm I} - \phi^{\rm I}\partial_n\phi)\mathrm{d}l
+ 2k_0 R \int_{-h}^{0} \left(\phi_0(z)\right)^2 \mathrm{d}z = 0,
}[/math]
For the present case the body is present only on the surface and we therefore have
[math]\displaystyle{
\phi_0(0) \int_{-L}^{L} e^{-k_0 x} \left(\alpha \phi(x) - \partial_n \phi(x)\right)\mathrm{d}x
+ 2k_0 R \int_{-h}^{0} \left(\phi_0(z)\right)^2 \mathrm{d}z = 0
}[/math]
Therefore
[math]\displaystyle{
R = -\frac{\int_{-L}^{L} e^{-k_0 x} \left(\alpha \phi(x) - \partial_n \phi(x)\right)\mathrm{d}x }
{2 k_0 \int_{-h}^{0} \left(\phi_0(z)\right)^2 \mathrm{d}z}.
}[/math]
and using a wave incident from the right we obtain
[math]\displaystyle{
T = 1 - \frac{\int_{-L}^{L} e^{k_0 x} \left(\alpha \phi(x) - \partial_n \phi(x)\right)\mathrm{d}x }
{2 k_0 \int_{-h}^{0} \left(\phi_0(z)\right)^2 \mathrm{d}z}.
}[/math]
Note that an expression for the integral in the denominator can be found in
Eigenfunction Matching for a Semi-Infinite Dock
