Example Calculations for the KdV and IST

Nonlinear PDE's Course
Current Topic	Example Calculations for the KdV and IST
Next Topic	Reaction-Diffusion Systems
Previous Topic	Connection betwen KdV and the Schrodinger Equation

We consider here the two examples we treated in Properties of the Linear Schrodinger Equation.

Example1: [math]\displaystyle{ \delta }[/math] function potential

We have already calculated the scattering data for the delta function potential in Properties of the Linear Schrodinger Equation. The scattering data is

[math]\displaystyle{ S\left( \lambda,0\right) =\left( k_{1},\sqrt{k_{1}},\frac{u_{0}}{2ik-u_{0} },\frac{2ik}{2ik-u_{0}}\right) }[/math]

The spectral data evolves as

[math]\displaystyle{ k_{1}=k_{1} }[/math] [math]\displaystyle{ c_{1}\left( t\right) =c_{1}\left( 0\right) e^{4k_{1}^{3}t}=\sqrt{k_{1} }e^{4k_{1}^{3}t} }[/math] [math]\displaystyle{ r\left( k,t\right) =r\left( k,0\right) e^{8ik^{3}t} }[/math] [math]\displaystyle{ a\left( k,t\right) =a\left( k,0\right) }[/math]

so that

[math]\displaystyle{ S\left( \lambda,t\right) =\left( k_{1},\sqrt{k_{1}}e^{4k_{1}^{3}t} ,\frac{u_{0}}{2ik-u_{0}}e^{8ik^{3}t},\frac{2ik}{2ik-u_{0}}\right) }[/math]

Example 2: Hat Function Potential

We solve for the case when

[math]\displaystyle{ u\left( x\right) =\left\{ \begin{matrix} 0, & x\notin\left[ -1,1\right] \\ 20, & x\in\left[ -1,1\right] \end{matrix} \right. }[/math]

We have already solved this case in Properties of the Linear Schrodinger Equation. For the even solutions we need to solve

[math]\displaystyle{ \tan\kappa=\frac{k}{\kappa} }[/math]

where [math]\displaystyle{ \kappa=\sqrt{b-k^{2}} }[/math].

For the odd solutions we need to solve and

[math]\displaystyle{ \tan\kappa=-\frac{\kappa}{k} }[/math]

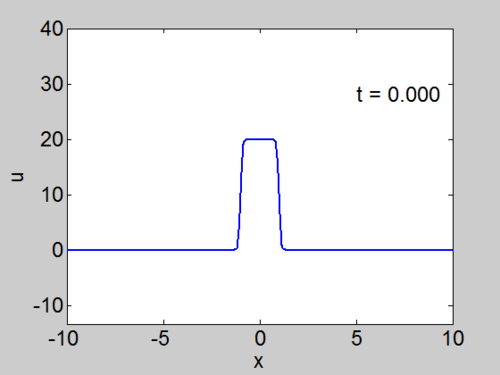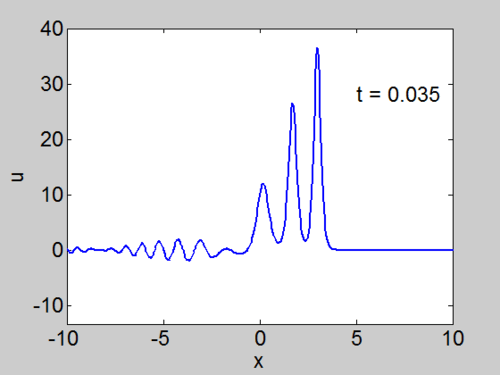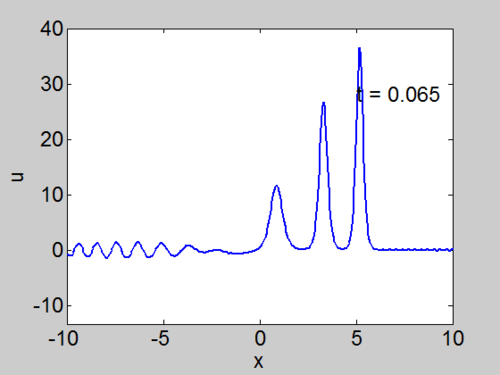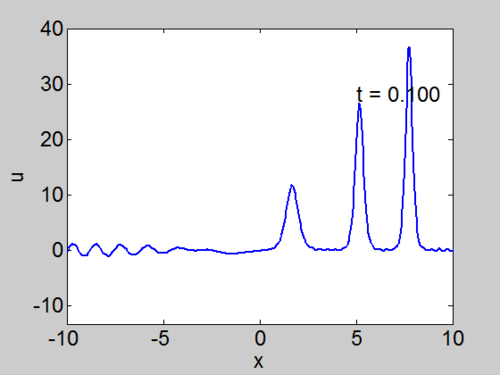
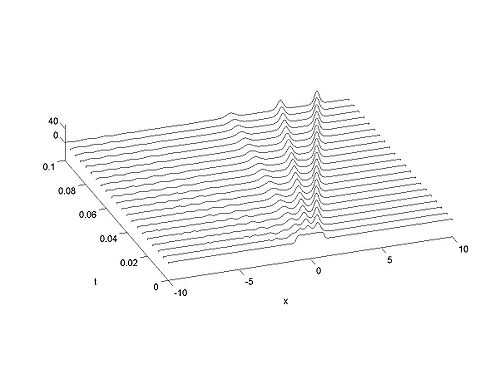
Recall that the solitons have amplitude [math]\displaystyle{ 2k_{n}^{2} }[/math] or [math]\displaystyle{ -2\lambda_{n} }[/math]. This can be seen in the height of the solitary waves.

We cannot work with a hat function numerically, because the jump in [math]\displaystyle{ u }[/math] leads to high frequencies which dominate the response.. We can smooth our function by a number of methods. We use here the function [math]\displaystyle{ \tanh\left( x\right) }[/math] so we write

[math]\displaystyle{ u\left( x\right) =\frac{20}{2}\left( \tanh\left( \nu\left( x+1\right) \right) -\tanh\left( \nu\left( x-1\right) \right) \right) }[/math]

where [math]\displaystyle{ \nu }[/math] is an appropriate constant to make the function increase in value sufficiently rapidly but not too rapidly.

Animation	Three-dimensional plot.
Evolution of [math]\displaystyle{ u(x,t) }[/math].	Evolution of [math]\displaystyle{ u(x,t) }[/math]