Eigenfunction Matching for a Semi-Infinite Floating Elastic Plate
Introduction
We show here a solution for a semi-infinite Floating Elastic Plate on Finite Depth. The problem was solved by Fox and Squire 1994 but the solution method here is slightly different. The simpler theory for a Dock describes many of the ideas here in more detail.
Equations
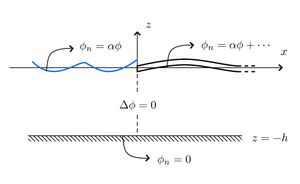
We consider the problem of small-amplitude waves which are incident on a semi-infinite floating elastic plate occupying water surface for [math]\displaystyle{ x\gt 0 }[/math]. The submergence of the plate is considered negligible. We assume that the problem is invariant in the [math]\displaystyle{ y }[/math] direction, although we allow the waves to be incident from an angle. We also assume that the plate edges are free to move at each boundary, although other boundary conditions could easily be considered using the methods of solution presented here. We begin with the Frequency Domain Problem for a semi-infinite Floating Elastic Plates in the non-dimensional form of Tayler 1986 (Dispersion Relation for a Floating Elastic Plate). We also assume that the waves are normally incident (incidence at an angle will be discussed later).
where [math]\displaystyle{ \alpha = \omega^2 }[/math], [math]\displaystyle{ \beta }[/math] and [math]\displaystyle{ \gamma }[/math] are the stiffness and mass constant for the plate respectively. The free edge conditions at the edge of the plate imply
Method of solution
Eigenfunction expansion
We will solve the system of equations using an Eigenfunction Matching Method. The method was developed by Fox and Squire 1994. The separation of variables for the left hand region where there is open water, and the incident wave, is described in Eigenfunction Matching for a Semi-Infinite Dock and we consider here only the separation of variables in the plate covered region.
Separation of variables under the Plate
The potential velocity can be written in terms of an infinite series of separated eigenfunctions under each elastic plate, of the form
If we apply the boundary conditions given we obtain the Dispersion Relation for a Floating Elastic Plate
Solving for [math]\displaystyle{ \kappa }[/math] gives a pure imaginary root with positive imaginary part, two complex roots (two complex conjugate paired roots with positive imaginary part in most physical situations), an infinite number of positive real roots which approach [math]\displaystyle{ {n\pi}/{h} }[/math] as [math]\displaystyle{ n }[/math] approaches infinity, and also the negative of all these roots (Dispersion Relation for a Floating Elastic Plate) . We denote the two complex roots with positive imaginary part by [math]\displaystyle{ \kappa_(-2) }[/math] and [math]\displaystyle{ \kappa_(-1) }[/math], the purely imaginary root with positive imaginary part by [math]\displaystyle{ \kappa_{0} }[/math] and the real roots with positive imaginary part by [math]\displaystyle{ \kappa_(n) }[/math] for [math]\displaystyle{ n }[/math] a positive integer. The imaginary root with positive imaginary part corresponds to a reflected travelling mode propagating along the [math]\displaystyle{ x }[/math] axis. The complex roots with positive imaginary parts correspond to damped reflected travelling modes and the real roots correspond to reflected evanescent modes.
Expressions for the potential velocity
We now expand the potential in the two regions using the separation of variables solution. We define
[math]\displaystyle{ \phi_{m}\left( z\right) =\frac{\cos k_{m}(z+H)}{\cos k_{m}H},\quad m\geq0 }[/math]
as the vertical eigenfunction of the potential in the open water region and
[math]\displaystyle{ \psi_{m}\left( z\right) =\frac{\cos\kappa_{m}(z+H)}{\cos\kappa_{m}H},\quad m\geq-2 }[/math]
as the vertical eigenfunction of the potential in the plate covered region. The potential [math]\displaystyle{ \phi }[/math] can now be expressed as the following sum of eigenfunctions: be expanded as
[math]\displaystyle{ \phi(x,z)= e^{-k_{0}x}\phi_{0}(z) + \sum_{m=0}^{\infty}a_{m}e^{k_{m}x}\phi_{m}(z), \;\;x\lt 0 }[/math]
and
[math]\displaystyle{ \phi(x,z)=\sum_{m=-2}^{\infty}b_{m} e^{-\kappa_{m}x}\psi_{m}(z), \;\;x\gt 0 }[/math]
where [math]\displaystyle{ a_{m} }[/math] and [math]\displaystyle{ b_{m} }[/math] are the coefficients to be determined.
For later reference, we note that:
[math]\displaystyle{ \int\nolimits_{-H}^{0}\phi_{m}(z)\phi_{n}(z) d z=A_{m}\delta_{mn} }[/math]
where
[math]\displaystyle{ A_{m}=\frac{1}{2}\left( \frac{\cos k_{m}H\sin k_{m}H+k_{m}H}{k_{m}\cos ^{2}k_{m}H}\right) }[/math]
and
[math]\displaystyle{ \int\nolimits_{-H}^{0}\phi_{n}(z)\psi_{m}(z) d z=B_{mn} }[/math]
where
An infinite dimensional system of equations
The potential and its derivative must be continuous across the transition from open water to the plate covered region. Therefore, the potentials and their derivatives at [math]\displaystyle{ x=0 }[/math] have to be equal. We also truncate the sum at [math]\displaystyle{ N }[/math] being careful that we have two extra modes on the plate covered region to satisfy the edge conditions. We obtain
[math]\displaystyle{ \phi_{0}\left( z\right) + \sum_{m=0}^{N} a_{m} \phi_{m}\left( z\right) =\sum_{m=-2}^{N}b_{m}\psi_{m}(z) }[/math]
and
[math]\displaystyle{ -k_{0}\phi_{0}\left( z\right) +\sum _{m=0}^{N} a_{m}k_{m}\phi_{m}\left( z\right) =-\sum_{m=-2}^{N}b_{m}\kappa_{m}\psi _{m}(z) }[/math]
for each [math]\displaystyle{ N }[/math]. We solve these equations by multiplying both equations by [math]\displaystyle{ \phi_{l}(z)\, }[/math] and integrating from [math]\displaystyle{ -h }[/math] to [math]\displaystyle{ 0 }[/math] to obtain:
[math]\displaystyle{ A_{0}\delta_{0l}+a_{l}A_{l} =\sum_{m=-2}^{N}b_{m}B_{ml},\,\,0 \leq l \leq N }[/math]
and
[math]\displaystyle{ -k_{0}A_{0}\delta_{0l}+a_{l}k_{l}A_l =-\sum_{m=-2}^{N}b_{m}\kappa_{m}B_{ml},\,\,0 \leq l \leq N }[/math]
If we multiply the first equation by [math]\displaystyle{ k_l }[/math] and subtract the second equation we obtain
[math]\displaystyle{ 2k_{0}A_{0}\delta_{0l} =\sum_{m=-2}^{N}b_{m}(k_l + \kappa_{m})B_{ml} }[/math]
Finally, we need to apply the conditions at the edge of the plate to give us two further equations,
[math]\displaystyle{ \partial_x^2\partial_z\phi = - \sum_{m=-2}^{N}b_{m} \kappa_m^3 \tan\kappa_m h = 0 }[/math]
and
[math]\displaystyle{ \partial_x^3\partial_z\phi = \sum_{m=-2}^{N}b_{m} \kappa_m^4 \tan\kappa_m h = 0 }[/math]
Numerical Solution
To solve the system of equations previously defined we set the upper limit of [math]\displaystyle{ l }[/math] to be [math]\displaystyle{ N }[/math], as we already said before. In terms of matrix, we obtain
[math]\displaystyle{ \begin{bmatrix} \begin{bmatrix} A_0&0 \quad \cdots&0\\ 0&&\\ \vdots&A_l&\vdots\\ &&0\\ 0&\cdots \quad 0 &A_N \end{bmatrix} & \begin{bmatrix} -B_{-20}&-B_{-10}\\ &\\ \vdots&\vdots\\ &\\ -B_{-2N}&-B_{-1N} \end{bmatrix} & \begin{bmatrix} -B_{00}&\cdots&-B_{0N}\\ &&\\ \vdots&-B_{ml}&\vdots\\ &&\\ -B_{N0}&\cdots&-B_{NN} \end{bmatrix} \\ \begin{bmatrix} 0&&\cdots&&0\\ 0&&\cdots&&0 \end{bmatrix} & \begin{bmatrix} \kappa_{-2}^3\tan\kappa_{-2}h&\kappa_{-1}^3\tan\kappa_{-1}h\\ \kappa_{-2}^4\tan\kappa_{-2}h&\kappa_{-1}^4\tan\kappa_{-1}h \end{bmatrix} & \begin{bmatrix} \kappa_0^3\tan\kappa_0h&\cdots&\kappa_N^3\tan\kappa_Nh\\ \kappa_0^4\tan\kappa_0h&\cdots&\kappa_N^4\tan\kappa_Nh \end{bmatrix} \\ \begin{bmatrix} 0&&\cdots&&0\\ &&&&\\ \vdots&&\ddots&&\vdots\\ &&&&\\ 0&&\cdots&&0 \end{bmatrix} & \begin{bmatrix} (k_0+\kappa_{-2})B_{-20}&(k_0+\kappa_{-1})B_{-10}\\ &\\ \vdots&\vdots\\ &\\ (k_N+\kappa_{-2})B_{-2N}&(k_N+\kappa_{-1})B_{-1N} \end{bmatrix} & \begin{bmatrix} (k_0 + \kappa_0) \, B_{00}&\cdots&(k_N + \kappa_{0}) \, B_{0N}\\ &&\\ \vdots&(k_l + \kappa_{m}) \, B_{ml}&\vdots\\ &&\\ (k_0 + \kappa_N) \, B_{N0}&\cdots&(k_N + \kappa_{N}) \, B_{NN}\\ \end{bmatrix} \end{bmatrix} \begin{bmatrix} a_{0} \\ \\ \vdots \\ \\ a_N \\ b_{-2}\\ b_{-1}\\ b_{0}\\ \\ \vdots \\ \\ b_N \end{bmatrix} = \begin{bmatrix} - A_{0} \\ 0 \\ \vdots \\ \\ 0 \\ 0 \\ 0 \\ 2k_{0}A_{0} \\ 0 \\ \vdots \\ \\ 0 \end{bmatrix} }[/math]
We then simply need to solve the linear system of equations. Note that we can solve this equation for [math]\displaystyle{ b_n }[/math] first and then solve for [math]\displaystyle{ a_n }[/math]
Waves Incident at an Angle
We can consider the case of Waves Incident at an Angle [math]\displaystyle{ \theta }[/math]. The theory shows that we can introduce a wavenumber in the [math]\displaystyle{ y }[/math]-direction which express [math]\displaystyle{ k_y=k_0 \sin \theta }[/math].
It is shown that the potential can be expanded as
[math]\displaystyle{ \phi(x,z)=e^{-\hat{k}_0x}\phi_0(z)+\sum_{m=0}^{\infty}a_{m}e^{\hat{k}_{m}x}\phi_{m}(z), \;\;x\lt 0 }[/math]
and
[math]\displaystyle{ \phi(x,z)=\sum_{m=-2}^{\infty}b_{m} e^{-\hat{\kappa}_{m}x}\psi_{m}(z), \;\;x\gt 0 }[/math]
where [math]\displaystyle{ \hat{k}_{m} = \sqrt{k_m^2 - k_y^2} }[/math] and [math]\displaystyle{ \hat{\kappa}_{m} = \sqrt{\kappa_m^2 - k_y^2} }[/math] where we always take the positive real root or the root with positive imaginary part.
The edge conditions are also different and are
and
where [math]\displaystyle{ \nu }[/math] is Poisons ratio.
We can expend these edge conditions, which respectively gives
[math]\displaystyle{ -\sum_{m=-2}^{\infty}b_{m}\kappa_m (\hat{\kappa}_m^3-\hat{\kappa}_m k_y^2(2-\nu))\tan \kappa_m h=0 }[/math]
and
[math]\displaystyle{ -\sum_{m=-2}^{\infty}b_{m}\kappa_m (\hat{\kappa}_m^2-k_y^2\nu))\tan \kappa_m h=0 }[/math]
The equations are derived almost identically to those above and we obtain
[math]\displaystyle{ A_{0}\delta_{0l}+a_{l}A_{l} =\sum_{m=-2}^{\infty}b_{m}B_{ml} }[/math]
and
[math]\displaystyle{ -\hat{k_{0}}A_{0}\delta_{0l}+a_{l}\hat{k}_{l}A_l =-\sum_{m=-2}^{\infty}b_{m}\hat{\kappa}_{m}B_{ml} }[/math]
and these are solved exactly as before.
Energy Balance
The energy balance equation is (Energy Balance for Two Elastic Plates where the left-hand side plate is open water for our problem, so we need to take the stiffness of this plate equal to [math]\displaystyle{ 0 }[/math], so as to model water) given by
where [math]\displaystyle{ T=b_0 }[/math], [math]\displaystyle{ R=a_0 }[/math], and [math]\displaystyle{ D }[/math] is given by
where the index [math]\displaystyle{ 0 }[/math] refers to the travelling wave (imaginary root of the dispersion equation).
Matlab Code
A program to calculate the coefficients for the semi-infinite dock problems can be found here semiinfinite_plate.m
Additional code
This program requires