Eigenfunction Matching for a Submerged Semi-Infinite Dock
Introduction
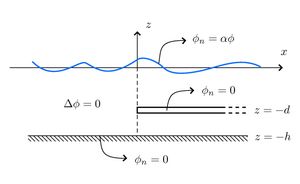
The problems consists of a region to the left with a free surface and a region to the right with a free surface and a submerged dock/plate through which not flow is possible. We begin with the simply problem when the waves are normally incident (so that the problem is truly two-dimensional). We then consider the case when the waves are incident at an angle. For the later we refer to the solution Eigenfunction Matching for a Semi-Infinite Dock
Governing Equations
We begin with the Frequency Domain Problem for the submerged dock in the region [math]\displaystyle{ x\gt 0 }[/math] (we assume [math]\displaystyle{ e^{i\omega t} }[/math] time dependence). The water is assumed to have constant finite depth [math]\displaystyle{ h }[/math] and the [math]\displaystyle{ z }[/math]-direction points vertically upward with the water surface at [math]\displaystyle{ z=0 }[/math] and the sea floor at [math]\displaystyle{ z=-h }[/math]. The boundary value problem can therefore be expressed as
[math]\displaystyle{ \Delta\phi=0, \,\, -h\lt z\lt 0, }[/math]
[math]\displaystyle{ \phi_{z}=0, \,\, z=-h, }[/math]
[math]\displaystyle{ \partial_z\phi=0, \,\, z=-d,\,x\gt 0, }[/math]
We must also apply the Sommerfeld Radiation Condition as [math]\displaystyle{ |x|\rightarrow\infty }[/math]. This essentially implies that the only wave at infinity is propagating away and at negative infinity there is a unit incident wave and a wave propagating away.
Solution Method
We use separation of variables in the three regions, [math]\displaystyle{ x\lt 0 }[/math] [math]\displaystyle{ -d\lt z\lt 0,\,\,x\gt 0 }[/math], and [math]\displaystyle{ -h\lt z\lt -d,\,\,x\gt 0 }[/math]. The first two regions use the free-surface eigenfunction and the third uses the dock eigenfunctions.
We express the potential as
[math]\displaystyle{ \phi(x,z) = X(x)Z(z)\, }[/math]
and then Laplace's equation becomes
[math]\displaystyle{ \frac{X^{\prime\prime}}{X} = - \frac{Z^{\prime\prime}}{Z} = k^2 }[/math]
Separation of variables for a free surface
We use separation of variables
We express the potential as
[math]\displaystyle{ \phi(x,z) = X(x)Z(z)\, }[/math]
and then Laplace's equation becomes
[math]\displaystyle{ \frac{X^{\prime\prime}}{X} = - \frac{Z^{\prime\prime}}{Z} = k^2 }[/math]
The separation of variables equation for deriving free surface eigenfunctions is as follows:
[math]\displaystyle{ Z^{\prime\prime} + k^2 Z =0. }[/math]
subject to the boundary conditions
[math]\displaystyle{ Z^{\prime}(-h) = 0 }[/math]
and
[math]\displaystyle{ Z^{\prime}(0) = \alpha Z(0) }[/math]
We can then use the boundary condition at [math]\displaystyle{ z=-h \, }[/math] to write
[math]\displaystyle{ Z = \frac{\cos k(z+h)}{\cos kh} }[/math]
where we have chosen the value of the coefficent so we have unit value at [math]\displaystyle{ z=0 }[/math]. The boundary condition at the free surface ([math]\displaystyle{ z=0 \, }[/math]) gives rise to:
which is the Dispersion Relation for a Free Surface
The above equation is a transcendental equation. If we solve for all roots in the complex plane we find that the first root is a pair of imaginary roots. We denote the imaginary solutions of this equation by [math]\displaystyle{ k_{0}=\pm ik \, }[/math] and the positive real solutions by [math]\displaystyle{ k_{m} \, }[/math], [math]\displaystyle{ m\geq1 }[/math]. The [math]\displaystyle{ k \, }[/math] of the imaginary solution is the wavenumber. We put the imaginary roots back into the equation above and use the hyperbolic relations
[math]\displaystyle{ \cos ix = \cosh x, \quad \sin ix = i\sinh x, }[/math]
to arrive at the dispersion relation
[math]\displaystyle{ \alpha = k\tanh kh. }[/math]
We note that for a specified frequency [math]\displaystyle{ \omega \, }[/math] the equation determines the wavenumber [math]\displaystyle{ k \, }[/math].
Finally we define the function [math]\displaystyle{ Z(z) \, }[/math] as
[math]\displaystyle{ \chi_{m}\left( z\right) =\frac{\cos k_{m}(z+h)}{\cos k_{m}h},\quad m\geq0 }[/math]
as the vertical eigenfunction of the potential in the open water region. From Sturm-Liouville theory the vertical eigenfunctions are orthogonal. They can be normalised to be orthonormal, but this has no advantages for a numerical implementation. It can be shown that
[math]\displaystyle{ \int\nolimits_{-h}^{0}\chi_{m}(z)\chi_{n}(z) \mathrm{d} z=A_{n}\delta_{mn} }[/math]
where
[math]\displaystyle{ A_{n}=\frac{1}{2}\left( \frac{\cos k_{n}h\sin k_{n}h+k_{n}h}{k_{n}\cos ^{2}k_{n}h}\right). }[/math]
Separation of Variables for a Dock
The separation of variables equation for a floating dock
[math]\displaystyle{ Z^{\prime\prime} + k^2 Z =0, }[/math]
subject to the boundary conditions
[math]\displaystyle{ Z^{\prime} (-h) = 0, }[/math]
and
[math]\displaystyle{ Z^{\prime} (0) = 0. }[/math]
The solution is [math]\displaystyle{ k=\kappa_{m}= \frac{m\pi}{h} \, }[/math], [math]\displaystyle{ m\geq 0 }[/math] and
[math]\displaystyle{ Z = \psi_{m}\left( z\right) = \cos\kappa_{m}(z+h),\quad m\geq 0. }[/math]
We note that
[math]\displaystyle{ \int\nolimits_{-h}^{0}\psi_{m}(z)\psi_{n}(z) \mathrm{d} z=C_{m}\delta_{mn}, }[/math]
where
[math]\displaystyle{ C_{m} = \begin{cases} h,\quad m=0 \\ \frac{1}{2}h,\,\,\,m\neq 0 \end{cases} }[/math]
The depth above the plate is [math]\displaystyle{ d }[/math] and below the plate is [math]\displaystyle{ h-d }[/math]. We introduce a new dispersion value [math]\displaystyle{ \mu_n }[/math]:
[math]\displaystyle{ \mu_n = \begin{cases} k_n^{d},\qquad \qquad\mbox{for}\,\, 0 \leq n \leq N-M\\ n\pi/(h-d),\,\,\mbox{otherwise} \end{cases} }[/math]
where [math]\displaystyle{ k_n^{d} }[/math] are the roots of the Dispersion Relation for a Free Surface with depth [math]\displaystyle{ d }[/math]. We also order the roots with the first being the positive imaginary solution [math]\displaystyle{ k_0^{d} }[/math], the second being zero, then ordering by increasing size. We then define a new function
[math]\displaystyle{ \chi_n = \begin{cases} 0,\,\,\, \qquad-d\lt z\lt 0 \\ \psi_{n}(z),\,\,\,-h\lt z\lt -d \end{cases} }[/math]
or
[math]\displaystyle{ \chi_{n} = \begin{cases} \phi_{n}^{d}(z),\,\,\,-d\lt z\lt 0 \\ 0,\,\,\qquad-h\lt z\lt -d \end{cases} }[/math]
where
[math]\displaystyle{ \phi_{m}^{d}\left( z\right) =\frac{\cos k_{m}^{d}(z+d)}{\cos k_{m}^{d}d},\quad m\geq0 }[/math]
depending on whether the root [math]\displaystyle{ \mu_n }[/math] is above or below.
The incident potential is a wave of amplitude [math]\displaystyle{ A }[/math] in displacement travelling in the positive [math]\displaystyle{ x }[/math]-direction. The incident potential can therefore be written as
[math]\displaystyle{ \phi^{\mathrm{I}} =e^{-k_{0}x}\phi_{0}\left( z\right) }[/math]
The potential can be expanded as
[math]\displaystyle{ \phi(x,z)=e^{-k_{0}^h x}\phi_{0}^h\left( z\right) + \sum_{m=0}^{\infty}a_{m}e^{k_{m}^h x}\phi_{m}^h(z), \;\;x\lt 0 }[/math]
[math]\displaystyle{ \phi(x,z)= \sum_{m=0}^{\infty}b_{m} e^{-k_{m}^d (x)}\phi_{m}^d(z) , \;\;-d\lt z\lt 0,\,\,x\gt 0 }[/math]
and
[math]\displaystyle{ \phi(x,z)= \sum_{m=0}^{\infty}c_{m} e^{\kappa_{m} x}\psi_{m}(z) , \;\;-h\lt z\lt -d,\,\,x\gt 0 }[/math]
where [math]\displaystyle{ a_{m} }[/math] and [math]\displaystyle{ b_{m} }[/math] are the coefficients of the potential in the open water regions to the left and right and [math]\displaystyle{ c_m }[/math] are the coefficients under the dock covered region. We have an incident wave from the left. [math]\displaystyle{ k_n^l }[/math] are the roots of the Dispersion Relation for a Free Surface
We denote the positive imaginary solutions by [math]\displaystyle{ k_{0}^l }[/math] and the positive real solutions by [math]\displaystyle{ k_{m}^l }[/math], [math]\displaystyle{ m\geq1 }[/math] (ordered with increasing imaginary part) and [math]\displaystyle{ \kappa_{m}=m\pi/(h-d) }[/math]. We define
[math]\displaystyle{ \phi_{m}^l\left( z\right) = \frac{\cos k_{m}(z+l)}{\cos k_{m}l},\quad m\geq0 }[/math]
as the vertical eigenfunction of the potential in the open water regions and
[math]\displaystyle{ \psi_{m}\left( z\right) = \cos\kappa_{m}(z+h),\quad m\geq 0 }[/math]
as the vertical eigenfunction of the potential in the dock covered region. We define
[math]\displaystyle{ \int\nolimits_{-d}^{0}\phi_{m}^d(z)\phi_{n}^d(z) d z=A_{m}\delta_{mn} }[/math]
where
[math]\displaystyle{ A_{m}=\frac{1}{2}\left( \frac{\cos k_{m}d\sin k_{m}d+k_{m}d}{k_{m}\cos ^{2}k_{m}l}\right) }[/math]
[math]\displaystyle{ \int\nolimits_{-d}^{0}\phi_{n}^h(z)\phi_{m}^d(z) d z=B_{mn} }[/math]
and
[math]\displaystyle{ \int\nolimits_{-h}^{-d}\phi_{n}^h(z)\psi_{m}(z) d z=C_{mn} }[/math]
and
[math]\displaystyle{ \int\nolimits_{-h}^{-d}\psi_{m}(z)\psi_{n}(z) d z=D_{m}\delta_{mn} }[/math]
where
An infinite dimensional system of equations
The potential and its derivative must be continuous across the transition from open water to the dock region. Therefore, the potentials and their derivatives at [math]\displaystyle{ x=0 }[/math] have to be equal. We obtain
[math]\displaystyle{ \phi_{0}^h\left( z\right) + \sum_{m=0}^{\infty} a_{m} \phi_{m}^h\left( z\right) =\sum_{m=0}^{\infty}b_{m}\phi_{m}^d(z),\,\,\,-d\lt z\lt 0 }[/math]
[math]\displaystyle{ \phi_{0}^h\left( z\right) + \sum_{m=0}^{\infty} a_{m} \phi_{m}^h\left( z\right) =\sum_{m=0}^{\infty}c_{m}\psi_{m}(z),\,\,\,-h\lt z\lt -d }[/math]
[math]\displaystyle{ -k_0^h\phi_{0}^h\left( z\right) + \sum_{m=0}^{\infty} k_m^h a_{m} \phi_{m}^h\left( z\right) =\sum_{m=0}^{\infty}k_m^d b_{m}\phi_{m}^d(z),\,\,\,-d\lt z\lt 0 }[/math]
[math]\displaystyle{ -k_0^h\phi_{0}^h\left( z\right) + \sum_{m=0}^{\infty} k_m^h a_{m} \phi_{m}^h\left( z\right) =\sum_{m=0}^{\infty}\kappa_m c_{m}\psi_{m}(z),\,\,\,-h\lt z\lt -d }[/math]
Numerical Solution
The standard method to solve these equations (from Linton and Evans 1991) is to mutiply both equations by [math]\displaystyle{ \phi_{q}^d(z) }[/math] and integrating from [math]\displaystyle{ -d }[/math] to [math]\displaystyle{ 0 }[/math] or by multiplying both equations by [math]\displaystyle{ \psi_{r}(z) }[/math] and integrating from [math]\displaystyle{ -h }[/math] to [math]\displaystyle{ -d }[/math]. However, we use a different method, which is closer to the solution method for Eigenfunction Matching for a Semi-Infinite Dock which allows us to keep the computer code similar. These is no significant difference between the methods numerically and a close connection exists.
We truncate the sum to [math]\displaystyle{ N+1 }[/math] modes and introduce a new function
[math]\displaystyle{ \chi_n = \begin{cases} \psi_{n}(z),\,\,\,-h\lt z\lt -d \\ 0,\,\,\,-d\lt z\lt 0 \end{cases} }[/math]
for [math]\displaystyle{ 0 \leq n \leq M - 1 }[/math]
[math]\displaystyle{ \chi_{n+M} = \begin{cases} 0,\,\,\,-h\lt z\lt -d \\ \phi_{n}^{d}(z),\,\,\,-d\lt z\lt 0 \end{cases} }[/math]
for [math]\displaystyle{ 0 \leq n \leq N-M }[/math] and we choose the values of [math]\displaystyle{ N }[/math] so that we have the [math]\displaystyle{ N+1 }[/math] smallest values of [math]\displaystyle{ k_n }[/math] and [math]\displaystyle{ \kappa_n }[/math] (with the proviso that we have at least one from each).
We truncate the equations and write
[math]\displaystyle{ \phi_{0}^h\left( z\right) + \sum_{m=0}^{N} a_{m} \phi_{m}^h\left( z\right) =\sum_{m=0}^{N}b_{m} \chi_m, }[/math]
[math]\displaystyle{ -k_0^h\phi_{0}^h\left( z\right) + \sum_{m=0}^{\infty} k_m^h a_{m} \phi_{m}^h\left( z\right) =\sum_{m=0}^{N}k^{\prime}_m b_{m}\chi_{m} }[/math]
where [math]\displaystyle{ k^{\prime}_m }[/math] is either [math]\displaystyle{ k^{d}_q }[/math] or [math]\displaystyle{ \kappa_q }[/math] as appropriate.
We multiply each equation by [math]\displaystyle{ \phi_{q}^h(z) }[/math] and integrating from [math]\displaystyle{ -h }[/math] to [math]\displaystyle{ 0 }[/math] to obtain
[math]\displaystyle{ A_{0}\delta_{0q} + a_{q}A_{q} = \sum_{m=0}^{N} b_m B^{\prime}_{mq} }[/math]
[math]\displaystyle{ -k_{0}^h A_{0}\delta_{0q} + k_{q}^h a_{q}A_{q} = \sum_{m=0}^{N} k^{\prime}_m b_m B^{\prime}_{mq} }[/math]
where [math]\displaystyle{ B^{\prime}_{mq} }[/math] is made from [math]\displaystyle{ B_{mq} }[/math] or [math]\displaystyle{ C_{mq} }[/math] as appropriate.
Solution with Waves Incident at an Angle
We can consider the problem when the waves are incident at an angle [math]\displaystyle{ \theta }[/math] but this is not presented here. For details see Eigenfunction Matching for a Semi-Infinite Dock.
Matlab Code
A program to calculate the coefficients for the submerged semi-infinite dock problems can be found here submerged_semiinfinite_dock.m
Additional code
This program requires