Linear Plane Progressive Regular Waves

From WikiWaves
Jump to navigationJump to search


Introduction

Regular time-harmonic linear plane progressive waves are the fundamental building block in describing the propagation of surface wave disturbances in a deterministic and stochastic setting and in predicting the response of floating structures in a seastate.

Equations

Regular time-harmonic linear plane progressive waves satisfy the boundary-value problem (in water of constant Finite Depth)

[math]\displaystyle{ \frac{\partial^2\Phi_1}{\partial t^2} + g \frac{\partial\Phi_1}{\partial z} = 0,\,\,\, z=0 }[/math]
[math]\displaystyle{ \nabla^2\Phi_1 = 0,\,\,\, -h \lt z \lt 0 }[/math]
[math]\displaystyle{ \frac{\partial\Phi_1}{\partial z} = 0,\,\,\, z=-h }[/math]

The last condition imposes a zero normal flux condition across a sea floor of constant depth, [math]\displaystyle{ h }[/math]. It turns out that if the water is sufficiently deep the wave does not feel any effect from the sea floor and we can make the Infinite Depth assumption.

Propagating Wave

Propagating Wave

There are a number of ways to derive the propagating wave solution, but the simplest is to define the free surface elevation apriori as

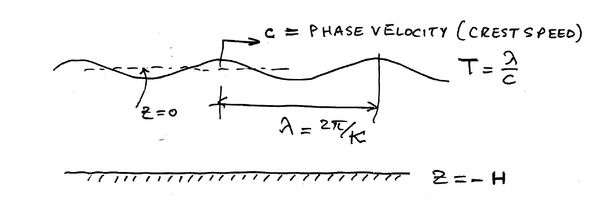
[math]\displaystyle{ \xi (x,t) = A \cos ( \omega t - k x) = A \mathbf{Re} \{ e^{-ikx+i\omega t} \} }[/math]

where A is an apriori known wave amplitude and the wave frequency and wave number [math]\displaystyle{ (\omega, k) \, }[/math] pair have the same definitions as in all wave propagation problems, namely:

[math]\displaystyle{ T = \frac{2\pi}{\omega} = \mbox{Wave Period} }[/math]
[math]\displaystyle{ \lambda = \frac{2\pi}{k} = \mbox{Wave Length} }[/math]
[math]\displaystyle{ c= \frac{\omega}{k} = \mbox{Wave Phase Velocity} }[/math]

The relation between [math]\displaystyle{ \omega \, }[/math] and [math]\displaystyle{ k \, }[/math] is known as the dispersion relation often written in the form

[math]\displaystyle{ \omega = f (k) \,. }[/math]

[math]\displaystyle{ f(k) \, }[/math] depends on the physics of the wave propagation problem under study, surface ocean waves are dispersive since [math]\displaystyle{ f(k)\, }[/math] is a non linear function of [math]\displaystyle{ k \, }[/math] as we will shortly show.

Expression in terms of velocity potential

By virtue of the definition of the wave elevation of a plane progressive regular wave, we seek a compatible definition of the respective velocity potential. Let:

[math]\displaystyle{ \Phi_1 = A \mathbf{Re} \{ \phi (x,z) e^{i\omega t} \} }[/math]

The problem reduces to the definition of [math]\displaystyle{ \phi(x,z) \, }[/math] and the derivation of the appropriate dispersion relation between [math]\displaystyle{ \omega \, }[/math] and [math]\displaystyle{ k \, }[/math] so that the linear boundary value problem is satisfied. Remember that the equation requires that we consider the fluid potential rather than simply the free surface.

Before proceeding with the algebra, certain underlying principles are always at work:

  • Linear system theory states that when the input signal is [math]\displaystyle{ e^{i \omega t} \, }[/math] the output signal must also be harmonic and with the same frequency.
  • We assume that a solution always exists, otherwise the statement of the physical and/or mathematical boundary value problem is flawed. If we can find a solution in most cases it is the solution. So simply try out solutions that may make sense from the physical point of view.
  • If the boundary value problem is satisfied by a complex velocity potential then it is also satisfied by its real and imaginary parts.

In our case we will first derive the boundary value problem satisfied by the complex potential [math]\displaystyle{ \phi(x,z) \, }[/math] and then we will try the plausible representation:

[math]\displaystyle{ \phi (x,z) = \psi (z) e^{- i k x} \, }[/math]

It follows upon substitution in the boundary value problem satisfied by [math]\displaystyle{ \Phi_1 (x,z,t) \, }[/math] that [math]\displaystyle{ \phi (x,z) \, }[/math] is subject to:

[math]\displaystyle{ \begin{cases} - \omega^2 \phi + g \phi_z = 0,& z=0 \\ \nabla^2\phi = \phi_{xx} + \phi_{zz} = 0,& -h\lt z\lt 0 \\ \phi_z = 0,& z=-h \end{cases} }[/math]

Allowing for:

[math]\displaystyle{ \phi (x,z) = \psi(z) e^{-ikx} \, }[/math]

It follows that [math]\displaystyle{ \psi(z) \, }[/math] is subject to:

[math]\displaystyle{ \begin{cases} - \omega^2 \psi + g \psi_z = 0,& z=0 \\ \psi_{zz} - k^2\psi = 0,& -h\lt z\lt 0 \\ \psi_z = 0,& z=-h \end{cases} }[/math]

We can verify by simple substitution that

[math]\displaystyle{ \psi(z) = \frac{ig}{\omega} \frac{\cosh k(z+h)}{\cosh k h} }[/math]

satisfies the field equation [math]\displaystyle{ \psi_{zz} - k^2 \psi = 0 \, }[/math], the seafloor condition [math]\displaystyle{ \psi_z=0, \, z=-h }[/math], and the free surface condition, only when

[math]\displaystyle{ \omega^2 = g k \tanh kh \, }[/math]

or

[math]\displaystyle{ \omega = \{ gk \tanh k h \}^{1/2} \, }[/math]

So by enforcing the free surface condition we have derived the Dispersion Relation for a Free Surface in Finite Depth.

The resulting plane progressive wave velocity potential takes the form:

[math]\displaystyle{ \phi_1 (x,z,t) = A \ \mathbf{Re} \left\{ \frac{ig}{\omega} \frac{\cosh k (z+h)}{\cosh k h} e^{ - i k x + i \omega t} \right\} }[/math]

This derivation is discussed in more mathematical depth in Eigenfunction Matching Method

Displacement and Pressure

Upon substitution we find

[math]\displaystyle{ \zeta = A \ \mathbf{Re} \{ e^{-ikx+i\omega t} \} = - \frac{1}{g} \left.\frac{\partial\phi_1}{\partial t} \right|_{z=0} }[/math]

The corresponding flow velocity at some point [math]\displaystyle{ \mathbf{x} = (x,z) }[/math] in the fluid domain or on [math]\displaystyle{ z=0, z=-h \, }[/math] is simply given by

[math]\displaystyle{ \mathbf{v_1} = \nabla \phi_1 }[/math]

The linear hydrodynamic pressure due to the plane progressive wave, which must be added to the hydrostatic, is

[math]\displaystyle{ P_1 = \rho \frac{\partial \phi_1}{\partial t} = \mathbf{Re} \left\{ \rho g A \frac{\cosh k (z+h)}{\cosh k h } e^{-ikx + i\omega t} \right\} }[/math]

From the Lagrangian kinematic relation

[math]\displaystyle{ \frac{d \zeta}{d t} = \mathbf{v}( \vec \xi_1, t) = \nabla \phi_1 ( \vec xi_1, t) }[/math]

We may obtain ordinary differential equations governing [math]\displaystyle{ \vec \xi_1 (t) }[/math]. Marking a paticular particle with the fluid at rest, so that [math]\displaystyle{ \vec \xi_1 (0) = \vec x }[/math], we may write:

[math]\displaystyle{ \vec \xi_1 (t) = \vec x + \vec {\Delta \xi (t)} }[/math]

Where [math]\displaystyle{ \vec x }[/math] is the particle position at rest and [math]\displaystyle{ \vec {\Delta\xi} }[/math] is its displacement due to the "arrival" of a plane progressive wave. Upon substitution in the equation of motion

[math]\displaystyle{ \frac{d \vec {\Delta\xi}}{dt} = \nabla \phi_1 (\vec x + \vec{\Delta\xi}, t) }[/math]

Since [math]\displaystyle{ \frac{d \vec x}{dt} = 0 }[/math]. Keeping terms of [math]\displaystyle{ \,O(\epsilon) }[/math] on both sides, it follows that

[math]\displaystyle{ \frac{d \vec{\Delta\xi}}{dt} = \nabla \phi_1 ( \vec x, t) + O (\epsilon^2) }[/math]

This equation when forced by the velocity vector that corresponds to the plane progressive wave solution derived above, leads to a harmonic solution for the particle displaced trajectories [math]\displaystyle{ \vec{\Delta\xi(t)} = (\Delta\xi_1, \Delta\xi_3) }[/math] which are circular.

If second-order effects are included, the particles under a plane progressive waves also undergo a steady-state drift known as the stokes drift. It can be easily modeled based on the approach described above by substituting second-order effects consistently into the right-hand side of the equation of motion (see Mh).

Dispersion Relation for a Free Surface in Deep and Shallow Waters

In Finite Depth

[math]\displaystyle{ \omega^2 = gk\tanh kh \, }[/math]

which is a nonlinear algebraic equation for [math]\displaystyle{ \omega\, }[/math] as a function of [math]\displaystyle{ k\, }[/math] which has a unique positive real solution as can be shown graphically. It also has imaginary roots which are important in many application (see Dispersion Relation for a Free Surface and Eigenfunction Matching Method) The unique positive real root [math]\displaystyle{ k \, }[/math] can only be found numerically. Yet it always exists and the iterative methods that may be implemented always converge rapidly. In deep water, [math]\displaystyle{ h \to \infty }[/math] and therefore

[math]\displaystyle{ \tanh kh \to 1 }[/math]

which in turn implies the deep water dispersion relation

[math]\displaystyle{ \omega^2 = g k \,. }[/math]

The phase speed is given by

[math]\displaystyle{ C = \frac{\omega}{k} = \frac{\omega}{\omega^2/g} = \frac{g}{\omega} = \frac{g}{2\pi/T} = \frac{gT}{2\pi} }[/math]

So the speed of the crest of a wave with period [math]\displaystyle{ \,T = 10 \mathrm{secs} }[/math] is approximately [math]\displaystyle{ 15.6 \,\mathrm{m/s} }[/math] or about 30 knots!

Often we need a quick estimate of the length of a deed water wave the period of which we can measure accurately with a stop watch. We proceed as follows:

[math]\displaystyle{ C = \frac{\omega}{k} = \frac{\lambda}{T} \ \Longrightarrow \ \frac{\lambda}{T} = \frac{g}{\omega} = \frac{g}{2\pi/T} \ \Longrightarrow \ \lambda = \frac{gT^2}{2\pi} \simeq T^2 + \frac{1}{2} T^2 }[/math]

(by definition the phase speed is the ration of the wave length over the period, or the time it takes for a crest to travel that distance). So the wave length of a deep water wave in m is approximately the square of its period is seconds plus half that amount. So a wave with period [math]\displaystyle{ T=10 }[/math] secs is about [math]\displaystyle{ 150 m }[/math] long.

In the limit of Shallow Depth [math]\displaystyle{ kh \to 0 }[/math] which in turn implies that

[math]\displaystyle{ \tanh kh \simeq kh }[/math]

It therefore follows that

[math]\displaystyle{ \omega^2 = gk (kh) \ \Longrightarrow \ \frac{\omega^2}{k^2} = gh }[/math]

or

[math]\displaystyle{ \frac{\omega}{k} = C = \sqrt{gh} }[/math]

Thus, according to linear theory shallow water waves become non dispersive as is the case with acoustic waves. Unfortunately, nonlinear effects become more important as waves propagate from deep to shallow water (because the wave amplidute rises). Solitons and wave breaking are some manifestations of nonlinearity.

The transition from deep to finite depth wave effects occurs for values of [math]\displaystyle{ kh \le \pi }[/math]. This is because

[math]\displaystyle{ \tanh \pi \simeq 1 }[/math]

and for [math]\displaystyle{ kh = \pi \ \Longrightarrow \ \frac{2\pi h}{\lambda} = \pi \ \Longrightarrow \ \frac{h}{\lambda} = \frac{1}{2} }[/math] so for [math]\displaystyle{ \frac{h}{\lambda} \gt \frac{1}{2} }[/math] or [math]\displaystyle{ kh \gt \pi }[/math] we are effectively dealing with Infinite Depth. This means that for most of the world ocean and wave conditions the water depth may be approximate as infinite.

This article is based on the MIT open course notes and the original article can be found here

Ocean Wave Interaction with Ships and Offshore Energy Systems

Retrieved from "https://wikiwaves.org/wiki/index.php?title=Linear_Plane_Progressive_Regular_Waves&oldid=8643"