The Reflection and Transmission Coefficients represent the ratio of the amplitude of the reflected or transmitted wave to the amplitude of the incident wave. They hold the property that [math]\displaystyle{ |R|^2+|T|^2=1\, }[/math] (and may often contain an imaginery element).
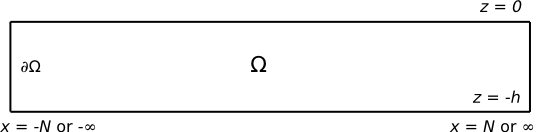
A diagram depicting the area
[math]\displaystyle{ \Omega\, }[/math] which is bounded by the rectangle
[math]\displaystyle{ \partial \Omega \, }[/math]. The rectangle
[math]\displaystyle{ \partial \Omega \, }[/math] is bounded by
[math]\displaystyle{ -h \leq z \leq 0 \, }[/math] and
[math]\displaystyle{ -\infty \leq x \leq \infty \, }[/math] or
[math]\displaystyle{ -N \leq x \leq N\, }[/math]We can calculate the Reflection and Transmission coefficients as follows:
Applying Green's theorem to [math]\displaystyle{ \phi\, }[/math] and [math]\displaystyle{ \phi^{\mathrm{I}}\, }[/math] gives:
[math]\displaystyle{
0 = \iint_{\Omega}(\phi\nabla^2\phi^{\mathrm{I}} - \phi^{\mathrm{I}}\nabla^2\phi)\mathrm{d}x\mathrm{d}z
= \int_{\partial\Omega}(\phi\frac{\partial\phi^{\rm I}}{\partial n} - \phi^{\rm I}\frac{\partial\phi}{\partial n})\mathrm{d}l,
}[/math]
[math]\displaystyle{
= \phi_0(0) \int_{-L}^{L} e^{k_0 x} \left(\alpha \phi(x) - \partial_n \phi(x)\right)\mathrm{d}x
- 2k_0 R \int_{-h}^{0} \left(\phi_0(z)\right)^2 \mathrm{d}z.
}[/math]<br\>
where [math]\displaystyle{ k_0 \, }[/math] is the first imaginery root of the dispersion equation and the incident wave is of the form: [math]\displaystyle{ \phi^I=\phi_0(z)e^{-ikx} \, }[/math]<br\><br\>
Therefore, in the case of a floating plate (where z=0):
[math]\displaystyle{
R = \frac{\int_{-L}^{L} e^{k_0 x} \left(\alpha \phi(x) - \partial_n \phi(x)\right)\mathrm{d}x }
{2 k_0 \int_{-h}^{0} \left(\phi_0(z)\right)^2 \mathrm{d}z}.
}[/math]
and using a wave incident from the right we obtain
[math]\displaystyle{
1 + T = \frac{\int_{-L}^{L} e^{-k_0 x} \left(\alpha \phi(x) - \partial_n \phi(x)\right)\mathrm{d}x }
{2 k_0 \int_{-h}^{0} \left(\phi_0(z)\right)^2 \mathrm{d}z}.
}[/math]
