Category:Wave Scattering in the Marginal Ice Zone
Introduction
The marginal ice zone (MIZ) is an interfacial region that forms at the boundary of the open and frozen oceans. Essentially it is a the region which is neither open ocean or frozen ocean, consisting of a patchwork of ice floes and open water. Wave processes are very important in the MIZ because waves facture the continuous ice and simultaneously the region of broken ice scatters wave energy protecting the interior of the ice from further wave induced fracture. The major way in which the open ocean interacts with the continuous ice is through wave induced breaking, and it is this process which produces the MIZ. However, wave action does not break up the continuous ice over an infinite distance. Instead, the wave energy is dissipated by scattering from the ice floes which have formed in the MIZ. The MIZ is thus formed by wave induced breaking of the continuous ice and simultaneously shields the continuous ice from breaking. There are two aspects which need to be understood to model this process: the first is the wave induced breaking of the continuous ice, and the second is the wave scattering in the MIZ (Squire et. al. 1995).
The experimental studies of wave propagation in the MIZ reported in \cite{directional86} and \cite{attenuation88} have shown the following features. There is strong exponential attenuation of energy, which decreases as the wave period increases. From a narrow directional spectrum at the ice edge the wave field broadens and becomes isotropic as it evolves with increasing distance into the MIZ.
Structure of the MIZ
The MIZ is generally tens to hundreds of kilometers deep. The structure varies dramatically depending on incident wave energy, wind, ice structure etc. Generally is can be divided into bands with floe size increasing with penetration depth into the MIZ.
Models for Wave Scattering
Mass Loading Model
The Mass Loading Model of Ice simply includes the effect of the ice cover by adding an additional mass term.
Eddy Viscosity Model
Model proposed by Weber 1987 is based on a two layer fluid (this ice being the second layer). The top layer is a viscous Newtonian fluid.
Floe Collision Models
Models based on floe collisions have been proposed by Shen and Squire 1998
Elastic Plate Models
Large ice floes can be modelled as a Floating Elastic Plate see Ice as a Thin Elastic Plate for more details, (this idea goes back more than 100 years). For this reason much of the study of wave-interaction with floating thin plates has been motivated by the application to ice floes. However, there is a discussion of this problem in Stoker 1957 in relation to breakwaters and more recently there has been a very large study of this problem (especially, but by no means exclusively in Japan) motivated by the marine engineering application to VLFS.
The problem of wave scattering by a floating elastic plate of shallow draft is well understood and the major challenge in geophysics is to try and understand the scattering of wave energy and how this is related to the small scale scattering. The problem can be divided into two and three-dimensional models.
Two Dimensional Model
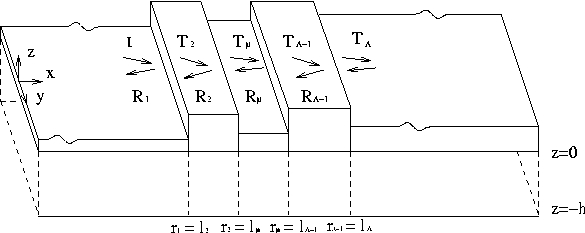
Figure 1: Schematic diagram of a wave propagating through a set of elastic plates.
Two dimensional wave scattering models in the MIZ have generally been studied in the context of a two-dimensional fluid covered by a finite number of elastic plates of possibly different properties. The problem is assumed to be invariant in the y direction, therefore reducing the problem to the dimensions in the x and z directions (Figure 1). The simplest problem to consider is one where there are only two semi-infinite plates of identical properties separated by a crack. A related problem in acoustics was considered by Kouzov 1963 who used an integral representation of the problem to solve it explicitly using the Riemann-Hilbert technique. Recently the crack problem has been considered by Squire and Dixon 2000 and Williams and Squire 2002 using a Green function method applicable to infinitely deep water and they obtained simple expressions for the reflection and transmission coefficients. Squire and Dixon 2001 extended the single crack problem to a multiple crack problem in which the semi-infinite regions are separated by a region consisting of a finite number of plates of finite size with all plates having identical properties. Evans and Porter 2005 further considered the multiple crack problem for finitely deep water and provided an explicit solution.
In parallel to the crack problem, the more challenging problem of two semi-infinite plates of different properties was considered. The first significant work on this problem was by Evans and Davies 1968 who present a solution method for evaluating the transmission and reflection of waves, in finitely deep water, propagating from a semi-infinite region of open water into a semi-infinite region of a floating elastic plate.
Although much simpler, the two-dimensional models have a number of advantages over the three-dimensional models, the most important being that it is much less computationally demanding. We also believe that a simple model is the best place to begin to make comparisons with data and to test and debug the more sophisticated models.
Three Dimensional Models
The most through study of this problem was by Masson and LeBlond 1989 who used transport theory to derive and equation for energy transport. Meylan, Squire and Fox 1997 independently derived a method based on the and an adhoc arguement. Meylan and Masson 2006 have shown that these two methods are nearly identical and have derived a Linear Boltzmann Model for Wave Scattering in the MIZ
Pages in category "Wave Scattering in the Marginal Ice Zone"
The following 4 pages are in this category, out of 4 total.