Difference between revisions of "Eigenfunction Matching for a Semi-Infinite Dock"
| (101 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | {{complete pages}} | |
| − | + | == Introduction == | |
| − | |||
| − | + | This is one of the simplest problem in eigenfunction matching. It also is an easy | |
| + | problem to understand the [[:Category:Wiener-Hopf|Wiener-Hopf]] and | ||
| + | [[:Category:Residue Calculus|Residue Calculus]]. The problems consists of a region to the left | ||
| + | with a free surface and a region to the right with a rigid surface through which | ||
| + | not flow is possible. | ||
| + | We begin with the simply problem when the waves are normally incident (so that | ||
| + | the problem is truly two-dimensional. We then consider the case when the waves are incident | ||
| + | at an angle. For the later we give the equations in slightly less detail. | ||
| + | The case of a [[Finite Dock]] is treated very similarly. The problem can also | ||
| + | be generalised to a [[ Eigenfunction Matching for Submerged Semi-Infinite Dock|Submerged Semi-Infinite Dock]] | ||
| − | + | [[Image:semiinfinite_dock.jpg|thumb|right|300px|Wave scattering by a semi-infinite dock]] | |
| − | |||
| − | |||
| − | =Governing Equations= | + | == Governing Equations == |
| − | We begin with the [[Frequency Domain Problem]] for a | + | We begin with the [[Frequency Domain Problem]] for a dock which occupies |
| − | + | the region <math>x>0</math> (we assume <math>e^{i\omega t}</math> time dependence). | |
| − | + | The water is assumed to have | |
| − | + | constant finite depth <math>h</math> and the <math>z</math>-direction points vertically | |
| − | + | upward with the water surface at <math>z=0</math> and the sea floor at <math>z=-h</math>. The | |
| − | constant finite depth <math> | ||
| − | upward with the water surface at <math>z=0</math> and the sea floor at <math>z=- | ||
boundary value problem can therefore be expressed as | boundary value problem can therefore be expressed as | ||
<center> | <center> | ||
<math> | <math> | ||
| − | \Delta\phi=0, \,\, - | + | \Delta\phi=0, \,\, -h < z < 0, |
</math> | </math> | ||
</center> | </center> | ||
<center> | <center> | ||
<math> | <math> | ||
| − | \ | + | \partial_z\phi=0, \,\, z=-h, |
</math> | </math> | ||
</center> | </center> | ||
<center><math> | <center><math> | ||
| − | \ | + | \partial_z\phi=\alpha\phi, \,\, z=0,\,x<0, |
</math></center> | </math></center> | ||
<center> | <center> | ||
<math> | <math> | ||
| − | + | \partial_z\phi=0, \,\, z=0,\,x>0, | |
</math> | </math> | ||
</center> | </center> | ||
| − | + | We | |
| − | + | must also apply the [[Sommerfeld Radiation Condition]] | |
| − | + | as <math>|x|\rightarrow\infty</math>. This essentially implies | |
| − | + | that the only wave at infinity is propagating away and at negative infinity there is a unit incident wave | |
| − | + | and a wave propagating away. | |
| − | + | ||
| − | + | == Solution Method == | |
| − | must also apply | ||
| − | as <math> | ||
| − | |||
| − | + | We use [http://en.wikipedia.org/wiki/Separation_of_Variables separation of variables] in the two regions, <math>x<0</math> | |
| + | and <math>x>0</math>. | ||
| − | + | {{separation of variables in two dimensions}} | |
| − | + | {{separation of variables for a free surface}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | surface | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {{separation of variables for a dock}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {{free surface dock relations}} | |
| − | + | === Expansion of the potential === | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | = | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | We need to apply some boundary conditions at plus and minus infinity, | |
| + | where are essentially the the solution cannot grow. This means that we | ||
| + | only have the positive (or negative) roots of the dispersion equation. | ||
| + | However, it does not help us with the purely imaginary root. Here we | ||
| + | must use a different condition, essentially identifying one solution | ||
| + | as the incoming wave and the other as the outgoing wave. | ||
| − | + | Therefore the scattered potential (without the incident wave, which will | |
| − | + | be added later) can | |
| − | + | be expanded as | |
<center> | <center> | ||
<math> | <math> | ||
| − | \ | + | \phi(x,z)=\sum_{m=0}^{\infty}a_{m}e^{k_{m}x}\phi_{m}(z), \;\;x<0 |
| − | |||
| − | |||
</math> | </math> | ||
</center> | </center> | ||
| Line 211: | Line 81: | ||
<center> | <center> | ||
<math> | <math> | ||
| − | \ | + | \phi(x,z)=\sum_{m=0}^{\infty}b_{m} |
| − | + | e^{-\kappa_{m}x}\psi_{m}(z), \;\;x>0 | |
| − | |||
</math> | </math> | ||
</center> | </center> | ||
| − | where <math> | + | where <math>a_{m}</math> and <math>b_{m}</math> |
| − | + | are the coefficients of the potential in the open water and | |
| − | + | the dock covered region respectively. | |
| − | + | ||
| − | + | {{incident potential for two dimensions}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | === An infinite dimensional system of equations === | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
The potential and its derivative must be continuous across the | The potential and its derivative must be continuous across the | ||
transition from open water to the plate covered region. Therefore, the | transition from open water to the plate covered region. Therefore, the | ||
| − | potentials and their derivatives at <math> | + | potentials and their derivatives at <math>x=0</math> have to be equal. |
| − | + | We obtain | |
<center> | <center> | ||
<math> | <math> | ||
| − | + | \phi_{0}\left( z\right) + \sum_{m=0}^{\infty} | |
| − | a_ | + | a_{m} \phi_{m}\left( z\right) |
| − | =\sum_{m= | + | =\sum_{m=0}^{\infty}b_{m}\psi_{m}(z) |
</math> | </math> | ||
</center> | </center> | ||
| Line 309: | Line 108: | ||
<center> | <center> | ||
<math> | <math> | ||
| − | + | -k_{0}\phi_{0}\left( z\right) +\sum | |
| − | _{m=0}^{\infty} a_ | + | _{m=0}^{\infty} a_{m}k_{m}\phi_{m}\left( z\right) |
| − | =\sum_{m= | + | =-\sum_{m=0}^{\infty}b_{m}\kappa_{m}\psi |
_{m}(z) | _{m}(z) | ||
</math> | </math> | ||
</center> | </center> | ||
| − | for each <math> | + | for each <math>m</math>. |
We solve these equations by multiplying both equations by | We solve these equations by multiplying both equations by | ||
| − | <math>\phi_{l}(z)</math> and integrating from <math>- | + | <math>\phi_{l}(z) \,</math> and integrating from <math>-h</math> to <math>0</math> to obtain: |
<center> | <center> | ||
<math> | <math> | ||
| − | + | A_{0}\delta_{0l}+a_{l}A_{l} | |
| − | =\sum_{m= | + | =\sum_{m=0}^{\infty}b_{m}B_{ml}\,\,\,(3) |
</math> | </math> | ||
</center> | </center> | ||
| Line 327: | Line 126: | ||
<center> | <center> | ||
<math> | <math> | ||
| − | + | -k_{0}A_{0}\delta_{0l}+a_{l}k_{l}A_l | |
| − | + | =-\sum_{m=0}^{\infty}b_{m}\kappa_{m}B_{ml} \,\,\,(4) | |
| − | =\sum_{m= | ||
| − | |||
</math> | </math> | ||
</center> | </center> | ||
| − | + | If we mutiply equation (3) by <math>k_l \,</math> and subtract equation (4) | |
| − | + | we obtain | |
<center> | <center> | ||
<math> | <math> | ||
| − | + | (k_{0}+k_l)A_{0}\delta_{0l} | |
| − | + | =\sum_{m=0}^{\infty}b_{m}(k_l + \kappa_{m})B_{ml} \,\,\,(5) | |
</math> | </math> | ||
</center> | </center> | ||
| − | + | This equation gives the required equations to solve for the | |
| − | ( | + | coefficients of the water velocity potential in the dock covered region. |
| + | |||
| + | == Numerical Solution == | ||
| + | |||
| + | To solve the system of equations (3) and (5), we set the upper limit of <math>l</math> to | ||
| + | be <math>M</math>. This resulting system can be expressed in the block matrix form below, | ||
<center> | <center> | ||
<math> | <math> | ||
| − | \ | + | \begin{bmatrix} |
| − | + | \begin{bmatrix} | |
| − | + | A_0&0 \quad \cdots&0\\ | |
| − | + | 0&&\\ | |
| − | + | \vdots&A_l&\vdots\\ | |
| + | &&0\\ | ||
| + | 0&\cdots \quad 0 &A_M | ||
| + | \end{bmatrix} | ||
| + | & | ||
| + | \begin{bmatrix} | ||
| + | -B_{00}&\cdots&-B_{0M}\\ | ||
| + | &&\\ | ||
| + | \vdots&-B_{ml}&\vdots\\ | ||
| + | &&\\ | ||
| + | -B_{M0}&\cdots&-B_{MM} | ||
| + | \end{bmatrix} | ||
| + | \\ | ||
| + | \begin{bmatrix} | ||
| + | 0&\cdots&0\\ | ||
| + | \vdots&\ddots&\vdots\\ | ||
| + | 0&\cdots&0 | ||
| + | \end{bmatrix} | ||
| + | & | ||
| + | \begin{bmatrix} | ||
| + | (k_0 + \kappa_0) \, B_{00}&\cdots&(k_M + \kappa_{0}) \, B_{0M}\\ | ||
| + | &&\\ | ||
| + | \vdots&(k_l + \kappa_{m}) \, B_{ml}&\vdots\\ | ||
| + | &&\\ | ||
| + | (k_0 + \kappa_M) \, B_{M0}&\cdots&(k_M + \kappa_{M}) \, B_{MM}\\ | ||
| + | \end{bmatrix} | ||
| + | \end{bmatrix} | ||
| + | \begin{bmatrix} | ||
| + | a_{0} \\ | ||
| + | a_{1} \\ | ||
| + | \vdots \\ | ||
| + | a_M \\ | ||
| + | \\ | ||
| + | b_{0}\\ | ||
| + | b_1 \\ | ||
| + | \vdots \\ | ||
| + | \\ | ||
| + | b_M | ||
| + | \end{bmatrix} | ||
| + | = | ||
| + | \begin{bmatrix} | ||
| + | - A_{0} \\ | ||
| + | 0 \\ | ||
| + | \vdots \\ | ||
| + | \\ | ||
| + | 0 \\ | ||
| + | \\ | ||
| + | 2k_{0}A_{0} \\ | ||
| + | 0 \\ | ||
| + | \vdots \\ | ||
| + | \\ | ||
| + | 0 | ||
| + | \end{bmatrix} | ||
</math> | </math> | ||
</center> | </center> | ||
| − | + | We then simply need to solve the linear system of equations. | |
| − | + | ||
| − | + | == Solution with Waves Incident at an Angle == | |
| − | + | ||
| + | We can consider the problem when the waves are incident at an angle <math>\theta</math>. | ||
| − | + | {{incident angle}} | |
| − | + | Therefore the potential can | |
| − | + | be expanded as | |
| − | |||
| − | |||
<center> | <center> | ||
<math> | <math> | ||
| − | \phi( | + | \phi(x,z)=e^{-\hat{k}_0x}\phi_0(z)+\sum_{m=0}^{\infty}a_{m}e^{\hat{k}_{m}x}\phi_{m}(z), \;\;x<0 |
| − | |||
</math> | </math> | ||
</center> | </center> | ||
| Line 372: | Line 224: | ||
<center> | <center> | ||
<math> | <math> | ||
| − | \phi( | + | \phi(x,z)=\sum_{m=0}^{\infty}b_{m} |
| − | _{m} | + | e^{-\hat{\kappa}_{m}x}\psi_{m}(z), \;\;x>0 |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
</math> | </math> | ||
</center> | </center> | ||
| + | where <math>\hat{k}_{m} = \sqrt{k_m^2 - k_y^2}</math> and <math>\hat{\kappa}_{m} = \sqrt{\kappa_m^2 - k_y^2}</math> | ||
| + | where we always take the positive real root or the root with positive imaginary part. | ||
| + | |||
| + | The equations are derived almost identically to those above and we obtain | ||
<center> | <center> | ||
<math> | <math> | ||
| − | + | A_{0}\delta_{0l}+a_{l}A_{l} | |
| − | \ | + | =\sum_{n=0}^{\infty}b_{m}B_{ml} |
| − | |||
| − | |||
</math> | </math> | ||
</center> | </center> | ||
| Line 401: | Line 241: | ||
<center> | <center> | ||
<math> | <math> | ||
| − | + | -\hat{k_{0}}A_{0}\delta_{0l}+a_{l}\hat{k}_{l}A_l | |
| − | + | =-\sum_{m=0}^{\infty}b_{m}\hat{\kappa}_{m}B_{ml} | |
| − | |||
| − | _{m} | ||
</math> | </math> | ||
</center> | </center> | ||
| − | + | and these are solved exactly as before. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | == Matlab Code == | |
| − | |||
| − | |||
| − | |||
| − | + | A program to calculate the coefficients for the semi-infinite dock problems can be found here | |
| − | + | {{semiinfinite_dock code}} | |
| − | |||
| − | |||
| − | |||
| − | + | === Additional code === | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | This program requires | ||
| + | * {{free surface dispersion equation code}} | ||
[[Category:Eigenfunction Matching Method]] | [[Category:Eigenfunction Matching Method]] | ||
Latest revision as of 00:43, 25 April 2017
Introduction
This is one of the simplest problem in eigenfunction matching. It also is an easy problem to understand the Wiener-Hopf and Residue Calculus. The problems consists of a region to the left with a free surface and a region to the right with a rigid surface through which not flow is possible. We begin with the simply problem when the waves are normally incident (so that the problem is truly two-dimensional. We then consider the case when the waves are incident at an angle. For the later we give the equations in slightly less detail. The case of a Finite Dock is treated very similarly. The problem can also be generalised to a Submerged Semi-Infinite Dock
Governing Equations
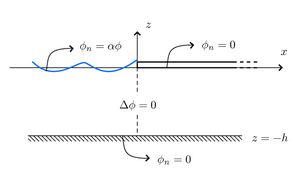
We begin with the Frequency Domain Problem for a dock which occupies the region [math]\displaystyle{ x\gt 0 }[/math] (we assume [math]\displaystyle{ e^{i\omega t} }[/math] time dependence). The water is assumed to have constant finite depth [math]\displaystyle{ h }[/math] and the [math]\displaystyle{ z }[/math]-direction points vertically upward with the water surface at [math]\displaystyle{ z=0 }[/math] and the sea floor at [math]\displaystyle{ z=-h }[/math]. The boundary value problem can therefore be expressed as
[math]\displaystyle{ \Delta\phi=0, \,\, -h \lt z \lt 0, }[/math]
[math]\displaystyle{ \partial_z\phi=0, \,\, z=-h, }[/math]
[math]\displaystyle{ \partial_z\phi=0, \,\, z=0,\,x\gt 0, }[/math]
We must also apply the Sommerfeld Radiation Condition as [math]\displaystyle{ |x|\rightarrow\infty }[/math]. This essentially implies that the only wave at infinity is propagating away and at negative infinity there is a unit incident wave and a wave propagating away.
Solution Method
We use separation of variables in the two regions, [math]\displaystyle{ x\lt 0 }[/math] and [math]\displaystyle{ x\gt 0 }[/math].
We express the potential as
[math]\displaystyle{ \phi(x,z) = X(x)Z(z)\, }[/math]
and then Laplace's equation becomes
[math]\displaystyle{ \frac{X^{\prime\prime}}{X} = - \frac{Z^{\prime\prime}}{Z} = k^2 }[/math]
Separation of variables for a free surface
We use separation of variables
We express the potential as
[math]\displaystyle{ \phi(x,z) = X(x)Z(z)\, }[/math]
and then Laplace's equation becomes
[math]\displaystyle{ \frac{X^{\prime\prime}}{X} = - \frac{Z^{\prime\prime}}{Z} = k^2 }[/math]
The separation of variables equation for deriving free surface eigenfunctions is as follows:
[math]\displaystyle{ Z^{\prime\prime} + k^2 Z =0. }[/math]
subject to the boundary conditions
[math]\displaystyle{ Z^{\prime}(-h) = 0 }[/math]
and
[math]\displaystyle{ Z^{\prime}(0) = \alpha Z(0) }[/math]
We can then use the boundary condition at [math]\displaystyle{ z=-h \, }[/math] to write
[math]\displaystyle{ Z = \frac{\cos k(z+h)}{\cos kh} }[/math]
where we have chosen the value of the coefficent so we have unit value at [math]\displaystyle{ z=0 }[/math]. The boundary condition at the free surface ([math]\displaystyle{ z=0 \, }[/math]) gives rise to:
which is the Dispersion Relation for a Free Surface
The above equation is a transcendental equation. If we solve for all roots in the complex plane we find that the first root is a pair of imaginary roots. We denote the imaginary solutions of this equation by [math]\displaystyle{ k_{0}=\pm ik \, }[/math] and the positive real solutions by [math]\displaystyle{ k_{m} \, }[/math], [math]\displaystyle{ m\geq1 }[/math]. The [math]\displaystyle{ k \, }[/math] of the imaginary solution is the wavenumber. We put the imaginary roots back into the equation above and use the hyperbolic relations
[math]\displaystyle{ \cos ix = \cosh x, \quad \sin ix = i\sinh x, }[/math]
to arrive at the dispersion relation
[math]\displaystyle{ \alpha = k\tanh kh. }[/math]
We note that for a specified frequency [math]\displaystyle{ \omega \, }[/math] the equation determines the wavenumber [math]\displaystyle{ k \, }[/math].
Finally we define the function [math]\displaystyle{ Z(z) \, }[/math] as
[math]\displaystyle{ \chi_{m}\left( z\right) =\frac{\cos k_{m}(z+h)}{\cos k_{m}h},\quad m\geq0 }[/math]
as the vertical eigenfunction of the potential in the open water region. From Sturm-Liouville theory the vertical eigenfunctions are orthogonal. They can be normalised to be orthonormal, but this has no advantages for a numerical implementation. It can be shown that
[math]\displaystyle{ \int\nolimits_{-h}^{0}\chi_{m}(z)\chi_{n}(z) \mathrm{d} z=A_{n}\delta_{mn} }[/math]
where
[math]\displaystyle{ A_{n}=\frac{1}{2}\left( \frac{\cos k_{n}h\sin k_{n}h+k_{n}h}{k_{n}\cos ^{2}k_{n}h}\right). }[/math]
Separation of Variables for a Dock
The separation of variables equation for a floating dock
[math]\displaystyle{ Z^{\prime\prime} + k^2 Z =0, }[/math]
subject to the boundary conditions
[math]\displaystyle{ Z^{\prime} (-h) = 0, }[/math]
and
[math]\displaystyle{ Z^{\prime} (0) = 0. }[/math]
The solution is [math]\displaystyle{ k=\kappa_{m}= \frac{m\pi}{h} \, }[/math], [math]\displaystyle{ m\geq 0 }[/math] and
[math]\displaystyle{ Z = \psi_{m}\left( z\right) = \cos\kappa_{m}(z+h),\quad m\geq 0. }[/math]
We note that
[math]\displaystyle{ \int\nolimits_{-h}^{0}\psi_{m}(z)\psi_{n}(z) \mathrm{d} z=C_{m}\delta_{mn}, }[/math]
where
[math]\displaystyle{ C_{m} = \begin{cases} h,\quad m=0 \\ \frac{1}{2}h,\,\,\,m\neq 0 \end{cases} }[/math]
Inner product between free surface and dock modes
[math]\displaystyle{ \int\nolimits_{-h}^{0}\phi_{n}(z)\psi_{m}(z) \mathrm{d} z=B_{mn} }[/math]
where
Expansion of the potential
We need to apply some boundary conditions at plus and minus infinity, where are essentially the the solution cannot grow. This means that we only have the positive (or negative) roots of the dispersion equation. However, it does not help us with the purely imaginary root. Here we must use a different condition, essentially identifying one solution as the incoming wave and the other as the outgoing wave.
Therefore the scattered potential (without the incident wave, which will be added later) can be expanded as
[math]\displaystyle{ \phi(x,z)=\sum_{m=0}^{\infty}a_{m}e^{k_{m}x}\phi_{m}(z), \;\;x\lt 0 }[/math]
and
[math]\displaystyle{ \phi(x,z)=\sum_{m=0}^{\infty}b_{m} e^{-\kappa_{m}x}\psi_{m}(z), \;\;x\gt 0 }[/math]
where [math]\displaystyle{ a_{m} }[/math] and [math]\displaystyle{ b_{m} }[/math] are the coefficients of the potential in the open water and the dock covered region respectively.
Incident potential
To create meaningful solutions of the velocity potential [math]\displaystyle{ \phi }[/math] in the specified domains we add an incident wave term to the expansion for the domain of [math]\displaystyle{ x \lt 0 }[/math] above. The incident potential is a wave of amplitude [math]\displaystyle{ A }[/math] in displacement travelling in the positive [math]\displaystyle{ x }[/math]-direction. We would only see this in the time domain [math]\displaystyle{ \Phi(x,z,t) }[/math] however, in the frequency domain the incident potential can be written as
[math]\displaystyle{ \phi_{\mathrm{I}}(x,z) =e^{-k_{0}x}\chi_{0}\left( z\right). }[/math]
The total velocity (scattered) potential now becomes [math]\displaystyle{ \phi = \phi_{\mathrm{I}} + \phi_{\mathrm{D}} }[/math] for the domain of [math]\displaystyle{ x \lt 0 }[/math].
The first term in the expansion of the diffracted potential for the domain [math]\displaystyle{ x \lt 0 }[/math] is given by
[math]\displaystyle{ a_{0}e^{k_{0}x}\chi_{0}\left( z\right) }[/math]
which represents the reflected wave.
In any scattering problem [math]\displaystyle{ |R|^2 + |T|^2 = 1 }[/math] where [math]\displaystyle{ R }[/math] and [math]\displaystyle{ T }[/math] are the reflection and transmission coefficients respectively. In our case of the semi-infinite dock [math]\displaystyle{ |a_{0}| = |R| = 1 }[/math] and [math]\displaystyle{ |T| = 0 }[/math] as there are no transmitted waves in the region under the dock.
An infinite dimensional system of equations
The potential and its derivative must be continuous across the transition from open water to the plate covered region. Therefore, the potentials and their derivatives at [math]\displaystyle{ x=0 }[/math] have to be equal. We obtain
[math]\displaystyle{ \phi_{0}\left( z\right) + \sum_{m=0}^{\infty} a_{m} \phi_{m}\left( z\right) =\sum_{m=0}^{\infty}b_{m}\psi_{m}(z) }[/math]
and
[math]\displaystyle{ -k_{0}\phi_{0}\left( z\right) +\sum _{m=0}^{\infty} a_{m}k_{m}\phi_{m}\left( z\right) =-\sum_{m=0}^{\infty}b_{m}\kappa_{m}\psi _{m}(z) }[/math]
for each [math]\displaystyle{ m }[/math]. We solve these equations by multiplying both equations by [math]\displaystyle{ \phi_{l}(z) \, }[/math] and integrating from [math]\displaystyle{ -h }[/math] to [math]\displaystyle{ 0 }[/math] to obtain:
[math]\displaystyle{ A_{0}\delta_{0l}+a_{l}A_{l} =\sum_{m=0}^{\infty}b_{m}B_{ml}\,\,\,(3) }[/math]
and
[math]\displaystyle{ -k_{0}A_{0}\delta_{0l}+a_{l}k_{l}A_l =-\sum_{m=0}^{\infty}b_{m}\kappa_{m}B_{ml} \,\,\,(4) }[/math]
If we mutiply equation (3) by [math]\displaystyle{ k_l \, }[/math] and subtract equation (4) we obtain
[math]\displaystyle{ (k_{0}+k_l)A_{0}\delta_{0l} =\sum_{m=0}^{\infty}b_{m}(k_l + \kappa_{m})B_{ml} \,\,\,(5) }[/math]
This equation gives the required equations to solve for the coefficients of the water velocity potential in the dock covered region.
Numerical Solution
To solve the system of equations (3) and (5), we set the upper limit of [math]\displaystyle{ l }[/math] to be [math]\displaystyle{ M }[/math]. This resulting system can be expressed in the block matrix form below,
[math]\displaystyle{ \begin{bmatrix} \begin{bmatrix} A_0&0 \quad \cdots&0\\ 0&&\\ \vdots&A_l&\vdots\\ &&0\\ 0&\cdots \quad 0 &A_M \end{bmatrix} & \begin{bmatrix} -B_{00}&\cdots&-B_{0M}\\ &&\\ \vdots&-B_{ml}&\vdots\\ &&\\ -B_{M0}&\cdots&-B_{MM} \end{bmatrix} \\ \begin{bmatrix} 0&\cdots&0\\ \vdots&\ddots&\vdots\\ 0&\cdots&0 \end{bmatrix} & \begin{bmatrix} (k_0 + \kappa_0) \, B_{00}&\cdots&(k_M + \kappa_{0}) \, B_{0M}\\ &&\\ \vdots&(k_l + \kappa_{m}) \, B_{ml}&\vdots\\ &&\\ (k_0 + \kappa_M) \, B_{M0}&\cdots&(k_M + \kappa_{M}) \, B_{MM}\\ \end{bmatrix} \end{bmatrix} \begin{bmatrix} a_{0} \\ a_{1} \\ \vdots \\ a_M \\ \\ b_{0}\\ b_1 \\ \vdots \\ \\ b_M \end{bmatrix} = \begin{bmatrix} - A_{0} \\ 0 \\ \vdots \\ \\ 0 \\ \\ 2k_{0}A_{0} \\ 0 \\ \vdots \\ \\ 0 \end{bmatrix} }[/math]
We then simply need to solve the linear system of equations.
Solution with Waves Incident at an Angle
We can consider the problem when the waves are incident at an angle [math]\displaystyle{ \theta }[/math].
When a wave in incident at an angle [math]\displaystyle{ \theta }[/math] we have the wavenumber in the [math]\displaystyle{ y }[/math] direction is [math]\displaystyle{ k_y = \sin\theta k_0 }[/math] where [math]\displaystyle{ k_0 }[/math] is as defined previously (note that [math]\displaystyle{ k_y }[/math] is imaginary).
This means that the potential is now of the form [math]\displaystyle{ \phi(x,y,z)=e^{k_y y}\phi(x,z) }[/math] so that when we separate variables we obtain
[math]\displaystyle{ k^2 = k_x^2 + k_y^2 }[/math]
where [math]\displaystyle{ k }[/math] is the separation constant calculated without an incident angle.
Therefore the potential can be expanded as
[math]\displaystyle{ \phi(x,z)=e^{-\hat{k}_0x}\phi_0(z)+\sum_{m=0}^{\infty}a_{m}e^{\hat{k}_{m}x}\phi_{m}(z), \;\;x\lt 0 }[/math]
and
[math]\displaystyle{ \phi(x,z)=\sum_{m=0}^{\infty}b_{m} e^{-\hat{\kappa}_{m}x}\psi_{m}(z), \;\;x\gt 0 }[/math]
where [math]\displaystyle{ \hat{k}_{m} = \sqrt{k_m^2 - k_y^2} }[/math] and [math]\displaystyle{ \hat{\kappa}_{m} = \sqrt{\kappa_m^2 - k_y^2} }[/math] where we always take the positive real root or the root with positive imaginary part.
The equations are derived almost identically to those above and we obtain
[math]\displaystyle{ A_{0}\delta_{0l}+a_{l}A_{l} =\sum_{n=0}^{\infty}b_{m}B_{ml} }[/math]
and
[math]\displaystyle{ -\hat{k_{0}}A_{0}\delta_{0l}+a_{l}\hat{k}_{l}A_l =-\sum_{m=0}^{\infty}b_{m}\hat{\kappa}_{m}B_{ml} }[/math]
and these are solved exactly as before.
Matlab Code
A program to calculate the coefficients for the semi-infinite dock problems can be found here semiinfinite_dock.m
Additional code
This program requires