Difference between revisions of "Eigenfunction Matching for a Semi-Infinite Dock"
| Line 153: | Line 153: | ||
</center> | </center> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==An infinite dimensional system of equations== | ==An infinite dimensional system of equations== | ||
Revision as of 03:18, 5 September 2006
Introduction
This is the simplest problem in eigenfunction matching. It also is an easy problem to understand the Wiener-Hopf and Residue Calculus
Introduction
We show here a solution for a Floating Elastic Plate on Finite Depth water based on Peter, Meylan and Chung 2004. A solution for Shallow Depth was given in Zilman and Miloh 2000 and we will also show this.
Governing Equations
We begin with the Frequency Domain Problem for a dock which occupies the region [math]\displaystyle{ x\gt 0 }[/math]. The water is assumed to have constant finite depth [math]\displaystyle{ H }[/math] and the [math]\displaystyle{ z }[/math]-direction points vertically upward with the water surface at [math]\displaystyle{ z=0 }[/math] and the sea floor at [math]\displaystyle{ z=-H }[/math]. The boundary value problem can therefore be expressed as
[math]\displaystyle{ \Delta\phi=0, \,\, -H\lt z\lt 0, }[/math]
[math]\displaystyle{ \phi_{z}=0, \,\, z=-H, }[/math]
[math]\displaystyle{ \phi_{z}=0, \,\, z=0,\,x\gt 0, }[/math]
We must also apply the Sommerfeld Radiation Condition as [math]\displaystyle{ |x|\rightarrow\infty }[/math]. The subscript [math]\displaystyle{ z }[/math] denotes the derivative in [math]\displaystyle{ z }[/math]-direction.
Solution Method
Separation of variables
We now separate variables and write the potential as
[math]\displaystyle{ \phi(x,z)=\zeta(z)\rho(x) }[/math]
Applying Laplace's equation we obtain
[math]\displaystyle{ \zeta_{zz}+\mu^{2}\zeta=0 }[/math]
so that:
[math]\displaystyle{ \zeta=\cos\mu(z+H) }[/math]
where the separation constant [math]\displaystyle{ \mu^{2} }[/math] must satisfy the Dispersion Relation for a Free Surface
[math]\displaystyle{ k\tan\left( kH\right) =-\alpha,\quad x\lt 0\,\,\,(1) }[/math]
and
[math]\displaystyle{ \kappa\tan(\kappa H)=0,\quad x\gt 0 \,\,\,(2) }[/math]
Note that we have set [math]\displaystyle{ \mu=k }[/math] under the free surface and [math]\displaystyle{ \mu=\kappa }[/math] under the plate. We denote the positive imaginary solution of (1) by [math]\displaystyle{ k_{0} }[/math] and the positive real solutions by [math]\displaystyle{ k_{m} }[/math], [math]\displaystyle{ m\geq1 }[/math]. The solutions of (2) [math]\displaystyle{ \kappa_{m}=m\pi/H }[/math], [math]\displaystyle{ m\geq 0 }[/math]. We define
[math]\displaystyle{ \phi_{m}\left( z\right) =\frac{\cos k_{m}(z+H)}{\cos k_{m}H},\quad m\geq0 }[/math]
as the vertical eigenfunction of the potential in the open water region and
[math]\displaystyle{ \psi_{m}\left( z\right) =\frac{\cos\kappa_{m}(z+H)}{\cos\kappa_{m}H},\quad m\geq 0 }[/math]
as the vertical eigenfunction of the potential in the plate covered region. For later reference, we note that:
[math]\displaystyle{ \int\nolimits_{-H}^{0}\phi_{m}(z)\phi_{n}(z) d z=A_{m}\delta_{mn} }[/math]
where
[math]\displaystyle{ A_{m}=\frac{1}{2}\left( \frac{\cos k_{m}H\sin k_{m}H+k_{m}H}{k_{m}\cos ^{2}k_{m}H}\right) }[/math]
and
[math]\displaystyle{ \int\nolimits_{-H}^{0}\phi_{n}(z)\psi_{m}(z) d z=B_{mn} }[/math]
where
Therefore the potential can be expanded as
[math]\displaystyle{ \phi(x,z)=\sum_{m=0}^{\infty}a_{m}e^{k_{m}x}\phi_{m}(z), \;\;x\lt 0 }[/math]
and
[math]\displaystyle{ \phi(x,z)=\sum_{m=0}^{\infty}b_{m} e^{-\kappa_{m}x}\psi_{m}(z), \;\;x\gt 0 }[/math]
where [math]\displaystyle{ a_{m} }[/math] and [math]\displaystyle{ b_{m} }[/math] are the coefficients of the potential in the open water and the plate covered region respectively.
Incident potential
The incident potential is a wave of amplitude [math]\displaystyle{ A }[/math] in displacement travelling in the positive [math]\displaystyle{ x }[/math]-direction. The incident potential can therefore be written as
[math]\displaystyle{ \phi^{\mathrm{I}} =e^{k_{0}x}\phi_{0}\left( z\right) }[/math]
An infinite dimensional system of equations
The boundary conditions (3) and (4) can be expressed in terms of the potential using (5). Since the angular modes are uncoupled the conditions apply to each mode, giving
[math]\displaystyle{ \sum_{m=-2}^{\infty}(\beta\kappa_{m}^{4}+1-\alpha\gamma)^{-1}b_{mn} \left(\kappa_{m}^{2}I_{n}(\kappa_{m}a)-\frac{1-\nu}{a}\left(\kappa _{m}I_{n}^{\prime}(\kappa_{m}a)-\frac{n^{2}}{a}I_{n}(\kappa_{m}a)\right) \right) =0\,\,\,(6) }[/math]
[math]\displaystyle{ \sum_{m=-2}^{\infty}(\beta\kappa_{m}^{4}+1-\alpha\gamma)^{-1}b_{mn} \left( \kappa_{m}^{3}I_{n}^{\prime}(\kappa_{m}a)+n^{2}\frac{1-\nu}{a^{2} }\left( \kappa_{m}I_{n}^{\prime}(\kappa_{m}a)+\frac{1}{a}I_{n}(\kappa _{m}a)\right) \right) =0\,\,\,(7) }[/math]
The potential and its derivative must be continuous across the transition from open water to the plate covered region. Therefore, the potentials and their derivatives at [math]\displaystyle{ r=a }[/math] have to be equal. Again we know that this must be true for each angle and we obtain
[math]\displaystyle{ e_{n}I_{n}(k_{0}a)\phi_{0}\left( z\right) + \sum_{m=0}^{\infty} a_{mn} K_{n}(k_{m}a)\phi_{m}\left( z\right) =\sum_{m=-2}^{\infty}b_{mn}I_{n}(\kappa_{m}a)\psi_{m}(z) }[/math]
and
[math]\displaystyle{ e_{n}k_{0}I_{n}^{\prime}(k_{0}a)\phi_{0}\left( z\right) +\sum _{m=0}^{\infty} a_{mn}k_{m}K_{n}^{\prime}(k_{m}a)\phi_{m}\left( z\right) =\sum_{m=-2}^{\infty}b_{mn}\kappa_{m}I_{n}^{\prime}(\kappa_{m}a)\psi _{m}(z) }[/math]
for each [math]\displaystyle{ n }[/math]. We solve these equations by multiplying both equations by [math]\displaystyle{ \phi_{l}(z) }[/math] and integrating from [math]\displaystyle{ -H }[/math] to [math]\displaystyle{ 0 }[/math] to obtain:
[math]\displaystyle{ e_{n}I_{n}(k_{0}a)A_{0}\delta_{0l}+a_{ln}K_{n}(k_{l}a)A_{l} =\sum_{m=-2}^{\infty}b_{mn}I_{n}(\kappa_{m}a)B_{ml} \,\,\,(8) }[/math]
and
[math]\displaystyle{ e_{n}k_{0}I_{n}^{\prime}(k_{0}a)A_{0}\delta_{0l}+a_{ln}k_{l}K_{n}^{\prime }(k_{l}a)A_{l} =\sum_{m=-2}^{\infty}b_{mn}\kappa_{m}I_{n}^{\prime}(\kappa_{m} a)B_{ml} \,\,\,(9) }[/math]
Equation (8) can be solved for the open water coefficients [math]\displaystyle{ a_{mn} }[/math]
[math]\displaystyle{ a_{ln}=-e_{n}\frac{I_{n}(k_{0}a)}{K_{n}(k_{0}a)}\delta_{0l}+\sum _{m=-2}^{\infty}b_{mn}\frac{I_{n}(\kappa_{m}a)B_{ml}}{K_{n}(k_{l}a)A_{l}} }[/math]
which can then be substituted into equation (9) to give us
[math]\displaystyle{ \left( k_{0}I_{n}^{\prime}(k_{0}a)-k_{0}\frac{K_{n}^{\prime}(k_{0} a)}{K_{n}(k_{0}a)}I_{n}(k_{0}a)\right) e_{n}A_{0}\delta_{0l} =\sum_{m=-2}^{\infty}\left( \kappa_{m}I_{n}^{\prime}(\kappa_{m} a)-k_{l}\frac{K_{n}^{\prime}(k_{l}a)}{K_{n}(k_{l}a)}I_{n}(\kappa _{m}a)\right) B_{ml}b_{mn}\,\,\,(10) }[/math]
for each [math]\displaystyle{ n }[/math]. Together with equations (6) and (7) equation (10) gives the required equations to solve for the coefficients of the water velocity potential in the plate covered region.
Numerical Solution
To solve the system of equations (10) together with the boundary conditions (6 and 7) we set the upper limit of [math]\displaystyle{ l }[/math] to be [math]\displaystyle{ M }[/math]. We also set the angular expansion to be from [math]\displaystyle{ n=-N }[/math] to [math]\displaystyle{ N }[/math]. This gives us
[math]\displaystyle{ \phi(r,\theta,z)=\sum_{n=-N}^{N}\sum_{m=0}^{M}a_{mn}K_{n}(k_{m}r)e^{i n\theta }\phi_{m}(z), \;\;r\gt a }[/math]
and
[math]\displaystyle{ \phi(r,\theta,z)=\sum_{n=-N}^{N}\sum_{m=-2}^{M}b_{mn}I_{n}(\kappa _{m}r)e^{i n\theta}\psi_{m}(z), \;\;r\lt a }[/math]
Since [math]\displaystyle{ l }[/math] is an integer with [math]\displaystyle{ 0\leq l\leq M }[/math] this leads to a system of [math]\displaystyle{ M+1 }[/math] equations. The number of unknowns is [math]\displaystyle{ M+3 }[/math] and the two extra equations are obtained from the boundary conditions for the free plate (6) and (7). The equations to be solved for each [math]\displaystyle{ n }[/math] are
[math]\displaystyle{ \left( k_{0}I_{n}^{\prime}(k_{0}a)-k_{0}\frac{K_{n}^{\prime}(k_{0} a)}{K_{n}(k_{0}a)}I_{n}(k_{0}a)\right) e_{n}A_{0}\delta_{0l} =\sum_{m=-2}^{M}\left( \kappa_{m}I_{n}^{\prime}(\kappa_{m}a)-k_{l} \frac{K_{n}^{\prime}(k_{l}a)}{K_{n}(k_{l}a)}I_{n}(\kappa_{m}a)\right) B_{ml}b_{mn} }[/math]
[math]\displaystyle{ \sum_{m=-2}^{M}(\beta\kappa_{m}^{4}+1-\alpha\gamma)^{-1}b_{mn} \left( \kappa_{m}^{2}I_{n}(\kappa_{m}a)-\frac{1-\nu}{a}\left( \kappa _{m}I_{n}^{\prime}(\kappa_{m}a)-\frac{n^{2}}{a}I_{n}(\kappa_{m}a)\right) \right) =0 }[/math]
and
[math]\displaystyle{ \sum_{m=-2}^{M}(\beta\kappa_{m}^{4}+1-\alpha\gamma)^{-1}b_{mn} \left( \kappa_{m}^{3}I_{n}^{\prime}(\kappa_{m}a)+n^{2}\frac{1-\nu}{a^{2} }\left( \kappa_{m}I_{n}^{\prime}(\kappa_{m}a)+\frac{1}{a}I_{n}(\kappa _{m}a)\right) \right) =0 }[/math]
It should be noted that the solutions for positive and negative [math]\displaystyle{ n }[/math] are identical so that they do not both need to be calculated. There are some minor simplifications which are a consequence of this which are discussed in more detail in Zilman and Miloh 2000.
The Shallow Depth Theory of Zilman and Miloh 2000
The shallow water theory of Zilman and Miloh 2000 can be recovered by simply setting the depth shallow enough that the shallow water theory is valid and setting [math]\displaystyle{ M=0 }[/math]. If the shallow water theory is valid then the first three roots of the dispersion equation for the ice will be exactly the same roots found in the shallow water theory by solving the polynomial equation. The system of equations has four unknowns (three under the plate and one in the open water) exactly as for the theory of Zilman and Miloh 2000.
Numerical Results
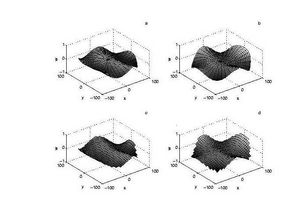
We present solutions for a plate of radius [math]\displaystyle{ a=100 }[/math]. The wavelength is [math]\displaystyle{ \lambda=50 }[/math] (recall that [math]\displaystyle{ \alpha=2\pi/\lambda\tanh\left( 2\pi H/\lambda\right) }[/math]), [math]\displaystyle{ \beta=10^{5} }[/math] and [math]\displaystyle{ \gamma=0 }[/math]. We compare with the method presented in Meylan 2002 for an arbitrary shaped plate modified to compute the solution for finite depth. The circle is represented in this scheme by square panels which are arranged to, as nearly as possible, form a circular shape.
Figure 1 shows the real part (a and c) and imaginary part (b and d) of the displacement for depth [math]\displaystyle{ H=25 }[/math]. The number of points in the angular expansion is [math]\displaystyle{ N=16 }[/math]. The number of roots of the dispersion equation is [math]\displaystyle{ M=8 }[/math]. Plots (a) and (b) are calculated using the circular plate method described here. Plots (c) and (d) are calculated using an arbitrary shaped plate method, with the panels shown being the actual panels used in the calculation. We see the expected agreement between the two methods.
The table below shows the values of the coefficients
[math]\displaystyle{ b_{mn} }[/math] for the case for previous case ([math]\displaystyle{ \lambda=50 }[/math],
[math]\displaystyle{ a=100 }[/math], [math]\displaystyle{ \beta=10^5 }[/math], [math]\displaystyle{ \gamma=0 }[/math], and [math]\displaystyle{ H=25 }[/math]). The very rapid
decay of the higher evanescent modes is apparent. This shows how efficient this method of
solution is since only a small number of modes are required.
[math]\displaystyle{ b_{mn} }[/math] [math]\displaystyle{ n=0 }[/math] [math]\displaystyle{ n=1 }[/math] [math]\displaystyle{ n=2 }[/math] [math]\displaystyle{ n=3 }[/math] [math]\displaystyle{ m=-2 }[/math] [math]\displaystyle{ 1.32 \!\times\!10^{-1}-9.71 \!\times\!10^{-1}i }[/math] [math]\displaystyle{ 6.85 \!\times\!10^{-1} -6.37 \!\times\!10^{-1}i }[/math] [math]\displaystyle{ 2.95 \!\times\!10^{-1}-1.12 \!\times\!10^{0}i }[/math] [math]\displaystyle{ 6.09 \!\times\!10^{-1} -4.95 \!\times\!10^{-1}i }[/math] [math]\displaystyle{ m=-1 }[/math] [math]\displaystyle{ -6.38 \!\times\!10^{-5}+1.47 \!\times\!10^{-3}i }[/math] [math]\displaystyle{ -3.92 \!\times\!10^{-3} + 3.99 \!\times\!10^{-3}i }[/math] [math]\displaystyle{ 1.41 \!\times\!10^{-3}+2.82 \!\times\!10^{-3}i }[/math] [math]\displaystyle{ -4.28 \!\times\!10^{-3} +3.89 \!\times\!10^{-3}i }[/math] [math]\displaystyle{ m=0 }[/math] [math]\displaystyle{ -3.29 \!\times\!10^{-4}+1.43 \!\times\!10^{-3}i }[/math] [math]\displaystyle{ 4.26 \!\times\!10^{-3} -3.62 \!\times\!10^{-3}i }[/math] [math]\displaystyle{ -2.62 \!\times\!10^{-3}+1.76 \!\times\!10^{-3}i }[/math] [math]\displaystyle{ 4.68 \!\times\!10^{-3} -3.39 \!\times\!10^{-3}i }[/math] [math]\displaystyle{ m=1 }[/math] [math]\displaystyle{ 4.31 \!\times\!10^{-7}-3.18 \!\times\!10^{-6}i }[/math] [math]\displaystyle{ -6.64 \!\times\!10^{-6} -7.14 \!\times\!10^{-6}i }[/math] [math]\displaystyle{ 2.07 \!\times\!10^{-7}-7.89 \!\times\!10^{-7}i }[/math] [math]\displaystyle{ -6.30 \!\times\!10^{-6} -7.74 \!\times\!10^{-6}i }[/math] [math]\displaystyle{ m=2 }[/math] [math]\displaystyle{ 6.79 \!\times\!10^{-13}-5.01 \!\times\!10^{-12}i }[/math] [math]\displaystyle{ -5.78 \!\times\!10^{-12}-6.21 \!\times\!10^{-12}i }[/math] [math]\displaystyle{ 8.87 \!\times\!10^{-13}-3.38 \!\times\!10^{-12}i }[/math] [math]\displaystyle{ -5.54 \!\times\!10^{-12}-6.81 \!\times\!10^{-12}i }[/math] [math]\displaystyle{ m=3 }[/math] [math]\displaystyle{ 1.35 \!\times\!10^{-18}-9.95 \!\times\!10^{-18}i }[/math] [math]\displaystyle{ -9.69 \!\times\!10^{-18}-1.04 \!\times\!10^{-17}i }[/math] [math]\displaystyle{ 1.94 \!\times\!10^{-18}-7.39 \!\times\!10^{-18}i }[/math] [math]\displaystyle{ -9.37 \!\times\!10^{-18}-1.15 \!\times\!10^{-17}i }[/math]