Difference between revisions of "Eigenfunction Matching for a Semi-Infinite Floating Elastic Plate"
Mike smith (talk | contribs) m (sign error (however is irrelevant as rhs = 0)) |
|||
| (118 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | =Introduction= | + | {{complete pages}} |
| + | |||
| + | == Introduction == | ||
We show here a solution for a semi-infinite [[:Category:Floating Elastic Plate|Floating Elastic Plate]] on [[Finite Depth]]. | We show here a solution for a semi-infinite [[:Category:Floating Elastic Plate|Floating Elastic Plate]] on [[Finite Depth]]. | ||
The problem was solved by [[Fox and Squire 1994]] but the solution method here is slightly different. | The problem was solved by [[Fox and Squire 1994]] but the solution method here is slightly different. | ||
| − | The simpler theory for a [[Eigenfunction Matching | + | The simpler theory for a [[Eigenfunction Matching for a Semi-Infinite Dock|Dock]] describes |
many of the ideas here in more detail. | many of the ideas here in more detail. | ||
| − | = Equations = | + | [[Image:Semiinfinite plate.jpg|thumb|right|300px|Wave scattering by a submerged semi-infinite elastic plate]] |
| + | |||
| + | == Equations == | ||
We consider the problem of small-amplitude waves which are incident on a semi-infinite floating elastic | We consider the problem of small-amplitude waves which are incident on a semi-infinite floating elastic | ||
| Line 18: | Line 22: | ||
in the non-dimensional form of [[Tayler_1986a|Tayler 1986]] ([[Dispersion Relation for a Floating Elastic Plate]]). | in the non-dimensional form of [[Tayler_1986a|Tayler 1986]] ([[Dispersion Relation for a Floating Elastic Plate]]). | ||
We also assume that the waves are normally incident (incidence at an angle will be discussed later). | We also assume that the waves are normally incident (incidence at an angle will be discussed later). | ||
| − | <center><math> | + | <center><math> |
\Delta \phi = 0, \;\;\; -h < z \leq 0, | \Delta \phi = 0, \;\;\; -h < z \leq 0, | ||
| − | + | </math></center> | |
<center><math> | <center><math> | ||
\partial_z \phi = 0, \;\;\; z = - h, | \partial_z \phi = 0, \;\;\; z = - h, | ||
| Line 29: | Line 33: | ||
<center><math> | <center><math> | ||
\beta \partial_x^4\partial_z \phi | \beta \partial_x^4\partial_z \phi | ||
| − | - \gamma\alpha \partial_z \phi | + | - \left( \gamma\alpha - 1 \right) \partial_z \phi = \alpha\phi, \;\; |
z = 0, \;\;\; x \geq 0, | z = 0, \;\;\; x \geq 0, | ||
</math></center> | </math></center> | ||
where <math>\alpha = \omega^2</math>, <math>\beta</math> and <math>\gamma</math> | where <math>\alpha = \omega^2</math>, <math>\beta</math> and <math>\gamma</math> | ||
| − | + | are the stiffness and mass constant for the plate respectively. The free edge conditions | |
| − | at the edge of the plate | + | at the edge of the plate imply |
<center><math> | <center><math> | ||
\partial_x^3 \partial_z\phi = 0, \;\; z = 0, \;\;\; x = 0, | \partial_x^3 \partial_z\phi = 0, \;\; z = 0, \;\;\; x = 0, | ||
| Line 42: | Line 46: | ||
</math></center> | </math></center> | ||
| − | =Method of solution= | + | == Method of solution == |
| − | + | We use [http://en.wikipedia.org/wiki/Separation_of_Variables separation of variables] in the two regions, <math>x<0</math> | |
| + | and <math>x>0</math>. | ||
| − | + | {{separation of variables in two dimensions}} | |
| − | |||
| − | |||
| − | |||
| − | + | {{separation of variables for a free surface}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {{separation of variables for a floating elastic plate}} | |
| − | + | {{free surface floating elastic plate relations}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | {{incident potential for two dimensions}} | ||
| + | == An infinite dimensional system of equations == | ||
| − | = | + | The potential and its derivative must be continuous across the |
| + | transition from open water to the plate covered region. Therefore, the | ||
| + | potentials and their derivatives at <math>x=0</math> have to be equal. | ||
| + | We also truncate the sum at <math>N</math> being careful that we have | ||
| + | two extra modes on the plate covered region to satisfy the edge conditions. | ||
| + | We obtain | ||
| + | <center> | ||
| + | <math> | ||
| + | \phi_{0}\left( z\right) + \sum_{m=0}^{N} | ||
| + | a_{m} \phi_{m}\left( z\right) | ||
| + | =\sum_{m=-2}^{N}b_{m}\psi_{m}(z) | ||
| + | </math> | ||
| + | </center> | ||
| + | and | ||
| + | <center> | ||
| + | <math> | ||
| + | -k_{0}\phi_{0}\left( z\right) +\sum | ||
| + | _{m=0}^{N} a_{m}k_{m}\phi_{m}\left( z\right) | ||
| + | =-\sum_{m=-2}^{N}b_{m}\kappa_{m}\psi | ||
| + | _{m}(z) | ||
| + | </math> | ||
| + | </center> | ||
| + | for each <math>N</math>. | ||
| + | We solve these equations by multiplying both equations by | ||
| + | <math>\phi_{l}(z)\,</math> and integrating from <math>-h</math> to <math>0</math> to obtain: | ||
| + | <center> | ||
| + | <math> | ||
| + | A_{0}\delta_{0l}+a_{l}A_{l} | ||
| + | =\sum_{m=-2}^{N}b_{m}B_{ml},\,\,0 \leq l \leq N | ||
| + | </math> | ||
| + | </center> | ||
| + | and | ||
| + | <center> | ||
| + | <math> | ||
| + | -k_{0}A_{0}\delta_{0l}+a_{l}k_{l}A_l | ||
| + | =-\sum_{m=-2}^{N}b_{m}\kappa_{m}B_{ml},\,\,0 \leq l \leq N | ||
| + | </math> | ||
| + | </center> | ||
| + | If we multiply the first equation by <math>k_l</math> and subtract the second equation | ||
| + | we obtain | ||
| + | <center> | ||
| + | <math> | ||
| + | (k_{0}+k_l)A_{0}\delta_{0l} | ||
| + | =\sum_{m=-2}^{N}b_{m}(k_l + \kappa_{m})B_{ml} | ||
| + | </math> | ||
| + | </center> | ||
| + | Finally, we need to apply the conditions at the edge of the plate to give us two further equations, | ||
| + | <center> | ||
| + | <math> | ||
| + | \partial_x^2\partial_z\phi = \sum_{m=-2}^{N}b_{m} \kappa_m^3 \tan\kappa_m h = 0 | ||
| + | </math> | ||
| + | </center> | ||
| + | and | ||
| + | <center> | ||
| + | <math> | ||
| + | \partial_x^3\partial_z\phi = - \sum_{m=-2}^{N}b_{m} \kappa_m^4 \tan\kappa_m h = 0 | ||
| + | </math> | ||
| + | </center> | ||
| − | + | == Numerical Solution == | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | <center><math>\begin{ | + | To solve the system of equations previously defined we set the upper limit of <math>l</math> to |
| − | \ | + | be <math>N</math>, as stated before. In terms of matrix, we obtain |
| − | \ | + | <center> |
| − | \end{ | + | <math> |
| − | + | \begin{bmatrix} | |
| − | \ | + | \begin{bmatrix} |
| − | \end{ | + | A_0&0 \quad \cdots&0\\ |
| − | + | 0&&\\ | |
| − | \ | + | \vdots&A_l&\vdots\\ |
| − | - \ | + | &&0\\ |
| − | \ | + | 0&\cdots \quad 0 &A_N |
| − | \end{ | + | \end{bmatrix} |
| − | + | & | |
| − | \ | + | \begin{bmatrix} |
| − | \ | + | -B_{-2,0}&-B_{-1,0}\\ |
| − | \end{ | + | &\\ |
| − | + | \vdots&\vdots\\ | |
| − | + | &\\ | |
| − | + | -B_{-2,N}&-B_{-1,N} | |
| − | + | \end{bmatrix} | |
| − | + | & | |
| − | \end{ | + | \begin{bmatrix} |
| − | + | -B_{0,0}&\cdots&-B_{0,N}\\ | |
| − | \ | + | &&\\ |
| − | \ | + | \vdots&-B_{m,l}&\vdots\\ |
| − | \ | + | &&\\ |
| + | -B_{N,0}&\cdots&-B_{N,N} | ||
| + | \end{bmatrix} | ||
| + | \\ \\ | ||
| + | \begin{bmatrix} | ||
| + | 0&&\cdots&&0\\ | ||
| + | 0&&\cdots&&0 | ||
| + | \end{bmatrix} | ||
| + | & | ||
| + | \begin{bmatrix} | ||
| + | \kappa_{-2}^3\tan\kappa_{-2}h&\kappa_{-1}^3\tan\kappa_{-1}h\\ | ||
| + | \kappa_{-2}^4\tan\kappa_{-2}h&\kappa_{-1}^4\tan\kappa_{-1}h | ||
| + | \end{bmatrix} | ||
| + | & | ||
| + | \begin{bmatrix} | ||
| + | \kappa_0^3\tan\kappa_0h&\cdots&\kappa_N^3\tan\kappa_Nh\\ | ||
| + | \kappa_0^4\tan\kappa_0h&\cdots&\kappa_N^4\tan\kappa_Nh | ||
| + | \end{bmatrix} | ||
| + | \\ \\ | ||
| + | \begin{bmatrix} | ||
| + | 0&&\cdots&&0\\ | ||
| + | &&&&\\ | ||
| + | \vdots&&\ddots&&\vdots\\ | ||
| + | &&&&\\ | ||
| + | 0&&\cdots&&0 | ||
| + | \end{bmatrix} | ||
| + | & | ||
| + | \begin{bmatrix} | ||
| + | (k_0+\kappa_{-2})B_{-2,0}&(k_0+\kappa_{-1})B_{-1,0}\\ | ||
| + | &\\ | ||
| + | \vdots&\vdots\\ | ||
| + | &\\ | ||
| + | (k_N+\kappa_{-2})B_{-2,N}&(k_N+\kappa_{-1})B_{-1,N} | ||
| + | \end{bmatrix} | ||
| + | & | ||
| + | \begin{bmatrix} | ||
| + | (k_0 + \kappa_0) \, B_{0,0}&\cdots&(k_N + \kappa_{0}) \, B_{0,N}\\ | ||
| + | &&\\ | ||
| + | \vdots&(k_l + \kappa_{m}) \, B_{m,l}&\vdots\\ | ||
| + | &&\\ | ||
| + | (k_0 + \kappa_N) \, B_{N,0}&\cdots&(k_N + \kappa_{N}) \, B_{N,N}\\ | ||
| + | \end{bmatrix} | ||
| + | \end{bmatrix} | ||
| + | \begin{bmatrix} | ||
| − | = | + | \begin{bmatrix} |
| + | a_{0} \\ | ||
| + | \\ | ||
| + | \vdots \\ | ||
| + | \\ | ||
| + | a_N | ||
| + | \end{bmatrix} | ||
| + | \\ \\ | ||
| + | \begin{bmatrix} | ||
| + | b_{-2}\\ | ||
| + | b_{-1} | ||
| + | \end{bmatrix} | ||
| + | \\ \\ | ||
| + | \begin{bmatrix} | ||
| + | b_{0}\\ | ||
| + | \\ | ||
| + | \vdots \\ | ||
| + | \\ | ||
| + | b_N | ||
| + | \end{bmatrix} | ||
| + | \end{bmatrix} | ||
| + | = | ||
| + | \begin{bmatrix} | ||
| + | \begin{bmatrix} | ||
| + | - A_{0} \\ | ||
| + | 0 \\ | ||
| + | \vdots \\ | ||
| + | \\ | ||
| + | 0 | ||
| + | \end{bmatrix} | ||
| + | \\ \\ | ||
| + | \begin{bmatrix} | ||
| + | 0 \\ | ||
| + | 0 | ||
| + | \end{bmatrix} | ||
| + | \\ \\ | ||
| + | \begin{bmatrix} | ||
| + | 2k_{0}A_{0} \\ | ||
| + | 0 \\ | ||
| + | \vdots \\ | ||
| + | \\ | ||
| + | 0 | ||
| + | \end{bmatrix} | ||
| + | \end{bmatrix} | ||
| + | </math> | ||
| + | </center> | ||
| + | We then simply need to solve the linear system of equations. Note that we can solve this equation for | ||
| + | <math>b_n</math> first and then solve for <math>a_n</math> | ||
| − | == | + | == Waves Incident at an Angle == |
| − | We | + | We can consider the case of [[Waves Incident at an Angle]] <math>\theta</math>. |
| − | + | {{incident angle}} | |
| − | |||
| − | |||
| − | + | It is shown that the potential can be expanded as | |
| − | + | <center> | |
| − | + | <math> | |
| − | <math>\phi = e^{\ | + | \phi(x,z)=e^{-\hat{k}_0x}\phi_0(z)+\sum_{m=0}^{\infty}a_{m}e^{\hat{k}_{m}x}\phi_{m}(z), \;\;x<0 |
| − | + | </math> | |
| − | + | </center> | |
| − | + | and | |
| − | + | <center> | |
| − | + | <math> | |
| − | + | \phi(x,z)=\sum_{m=-2}^{\infty}b_{m} | |
| − | + | e^{-\hat{\kappa}_{m}x}\psi_{m}(z), \;\;x>0 | |
| − | + | </math> | |
| − | + | </center> | |
| − | + | where <math>\hat{k}_{m} = \sqrt{k_m^2 - k_y^2}</math> and <math>\hat{\kappa}_{m} = \sqrt{\kappa_m^2 - k_y^2}</math> | |
| − | + | where we always take the positive real root or the root with positive imaginary part. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | where the | ||
| − | + | The edge conditions are also different and are | |
| − | + | <center><math> | |
| − | + | \left(\frac{\partial^3}{\partial x^3} + (2 - \nu)k^2_y\frac{\partial}{\partial x}\right) \frac{\partial\phi}{\partial z}= 0, | |
| − | + | </math></center> | |
| − | + | and | |
| − | |||
<center><math> | <center><math> | ||
| − | + | \left(\frac{\partial^2}{\partial x^2} + \nu k^2_y\right)\frac{\partial\phi}{\partial z} = 0, | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
</math></center> | </math></center> | ||
| − | + | where <math>\nu</math> is Poisons ratio. | |
| − | |||
| + | We can expend these edge conditions, which respectively gives | ||
| + | <center> | ||
| + | <math> | ||
| + | -\sum_{m=-2}^{\infty}b_{m}\kappa_m (\hat{\kappa}_m^3+\hat{\kappa}_m k_y^2(2-\nu))\tan \kappa_m h=0 | ||
| + | </math> | ||
| + | </center> | ||
| + | and | ||
| + | <center> | ||
| + | <math> | ||
| + | -\sum_{m=-2}^{\infty}b_{m}\kappa_m (\hat{\kappa}_m^2+k_y^2\nu))\tan \kappa_m h=0 | ||
| + | </math> | ||
| + | </center> | ||
| + | The equations are derived almost identically to those above and we obtain | ||
| + | <center> | ||
| + | <math> | ||
| + | A_{0}\delta_{0l}+a_{l}A_{l} | ||
| + | =\sum_{m=-2}^{\infty}b_{m}B_{ml} | ||
| + | </math> | ||
| + | </center> | ||
| + | and | ||
| + | <center> | ||
| + | <math> | ||
| + | -\hat{k_{0}}A_{0}\delta_{0l}+a_{l}\hat{k}_{l}A_l | ||
| + | =-\sum_{m=-2}^{\infty}b_{m}\hat{\kappa}_{m}B_{ml} | ||
| + | </math> | ||
| + | </center> | ||
| + | and these are solved exactly as before. | ||
| − | == | + | == Energy Balance == |
| − | + | We present a derivation of the energy balance here and also refer to the derivation | |
| − | We | + | [[Energy Balance for Two Elastic Plates]] |
| − | |||
| − | |||
| − | |||
| − | |||
| − | for | ||
| − | |||
| − | + | {{energy contour and preliminaries}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | The contributions from the vertical ends are | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<center><math> | <center><math> | ||
| − | \ | + | \lim_{x\to-\infty} \Im\int_{-h}^{0}\phi^*\frac{\partial\phi}{\partial n} dz |
| − | + | = \lim_{x\to-\infty} \Im\int_{-h}^{0} \hat{k}_0 \left(e^{\hat{k}_0 x} + a_0^{*} e^{-\hat{k}_0 x} \right) | |
| − | + | \left(e^{-\hat{k}_0 x} - a_0 e^{\hat{k}_0 x} \right)\phi_0(z)^2 dz | |
| − | \ | ||
</math></center> | </math></center> | ||
| − | |||
<center><math> | <center><math> | ||
| − | + | = \frac{\hat{k}_0}{i} A_0 \left(1 - |a_0^2| \right) | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
</math></center> | </math></center> | ||
and | and | ||
| − | |||
| − | |||
<center><math> | <center><math> | ||
| − | \ | + | \lim_{x\to\infty} \Im\int_{-h}^{0}\phi^*\frac{\partial\phi}{\partial n} dz |
| − | {\ | + | = \lim_{x\to\infty} \Im\int_{-h}^{0} -\hat{\kappa}_0 \left(b_0^{*} e^{\hat{\kappa}_0 x} \right) |
| − | {\ | + | \left(b_0 e^{-\hat{\kappa}_0 x}\right)\psi_0(z)^2 dz |
| − | |||
</math></center> | </math></center> | ||
| − | |||
<center><math> | <center><math> | ||
| − | {\ | + | = -\frac{\hat{\kappa}_0}{i} |b_0^2| \int_{-h}^{0} \psi_0(z)^2 dz |
</math></center> | </math></center> | ||
| − | The | + | The contribution from the surface integral under the plate is |
<center><math> | <center><math> | ||
| − | \ | + | \Im\int_{0}^{\infty}\phi^*\frac{\partial\phi}{\partial n} dx |
| − | {\ | + | = \Im\int_{0}^{\infty} |
| − | {\ | + | 1/\alpha \left(\beta \partial_x^4 \frac{\partial\phi^{*}}{\partial n} - (\gamma\alpha - 1 ) \frac{\partial\phi^{*}}{\partial n} \right) |
| − | \ | + | \frac{\partial\phi}{\partial n} dx |
</math></center> | </math></center> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<center><math> | <center><math> | ||
| − | + | = \frac{2\beta}{\alpha} \frac{\hat{\kappa}_0^{3}}{i} |b_0^2| \partial_z\psi_0(0)^2 | |
| − | |||
| − | { | ||
| − | {\ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
</math></center> | </math></center> | ||
| + | where we have integrated by parts and used the condition at the ends of the plate. | ||
| − | + | The energy balance is therefore | |
| − | |||
<center><math> | <center><math> | ||
| − | {\ | + | {\hat{k}_0} A_0 |a_0^2| + {\hat{\kappa}_0} |b_0^2| \int_{-h}^{0} \psi_0(z)^2 dz |
| − | + | - \frac{2\beta}{\alpha}{ \hat{\kappa}_0^{3}} |b_0^2| \partial_z\psi_0(0)^2 = {\hat{k}_0} A_0 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
</math></center> | </math></center> | ||
| − | |||
| − | + | Note that this formula is only valid for angles <math>\theta \in [-\theta_0, \theta_0]</math>, where <math>\theta_0</math> | |
| − | + | is defined by <math>\sin \theta_0 =\frac{\kappa_0}{k_0}</math>. For large angles there is total reflection | |
| − | \ | + | and then <math>|R|^2=1</math> |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </math | ||
| − | + | == Matlab Code == | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | A program to calculate the coefficients for the semi-infinite dock problems can be found here | |
| − | + | [http://www.math.auckland.ac.nz/~meylan/code/eigenfunction_matching/semiinfinite_plate.m semiinfinite_plate.m] | |
| − | |||
| − | - | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | === Additional code === | |
| − | |||
| − | |||
| − | |||
| − | |||
| + | This program requires | ||
| + | * {{free surface dispersion equation code}} | ||
| + | * {{elastic plate dispersion equation code}} | ||
[[Category:Floating Elastic Plate]] | [[Category:Floating Elastic Plate]] | ||
[[Category:Eigenfunction Matching Method]] | [[Category:Eigenfunction Matching Method]] | ||
| − | + | [[Category:Complete Pages]] | |
| − | [[Category: | ||
| − | |||
Latest revision as of 20:51, 17 March 2010
Introduction
We show here a solution for a semi-infinite Floating Elastic Plate on Finite Depth. The problem was solved by Fox and Squire 1994 but the solution method here is slightly different. The simpler theory for a Dock describes many of the ideas here in more detail.
Equations
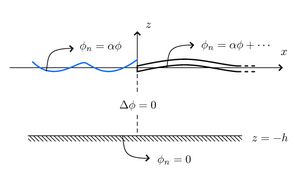
We consider the problem of small-amplitude waves which are incident on a semi-infinite floating elastic plate occupying water surface for [math]\displaystyle{ x\gt 0 }[/math]. The submergence of the plate is considered negligible. We assume that the problem is invariant in the [math]\displaystyle{ y }[/math] direction, although we allow the waves to be incident from an angle. We also assume that the plate edges are free to move at each boundary, although other boundary conditions could easily be considered using the methods of solution presented here. We begin with the Frequency Domain Problem for a semi-infinite Floating Elastic Plates in the non-dimensional form of Tayler 1986 (Dispersion Relation for a Floating Elastic Plate). We also assume that the waves are normally incident (incidence at an angle will be discussed later).
where [math]\displaystyle{ \alpha = \omega^2 }[/math], [math]\displaystyle{ \beta }[/math] and [math]\displaystyle{ \gamma }[/math] are the stiffness and mass constant for the plate respectively. The free edge conditions at the edge of the plate imply
Method of solution
We use separation of variables in the two regions, [math]\displaystyle{ x\lt 0 }[/math] and [math]\displaystyle{ x\gt 0 }[/math].
We express the potential as
[math]\displaystyle{ \phi(x,z) = X(x)Z(z)\, }[/math]
and then Laplace's equation becomes
[math]\displaystyle{ \frac{X^{\prime\prime}}{X} = - \frac{Z^{\prime\prime}}{Z} = k^2 }[/math]
Separation of variables for a free surface
We use separation of variables
We express the potential as
[math]\displaystyle{ \phi(x,z) = X(x)Z(z)\, }[/math]
and then Laplace's equation becomes
[math]\displaystyle{ \frac{X^{\prime\prime}}{X} = - \frac{Z^{\prime\prime}}{Z} = k^2 }[/math]
The separation of variables equation for deriving free surface eigenfunctions is as follows:
[math]\displaystyle{ Z^{\prime\prime} + k^2 Z =0. }[/math]
subject to the boundary conditions
[math]\displaystyle{ Z^{\prime}(-h) = 0 }[/math]
and
[math]\displaystyle{ Z^{\prime}(0) = \alpha Z(0) }[/math]
We can then use the boundary condition at [math]\displaystyle{ z=-h \, }[/math] to write
[math]\displaystyle{ Z = \frac{\cos k(z+h)}{\cos kh} }[/math]
where we have chosen the value of the coefficent so we have unit value at [math]\displaystyle{ z=0 }[/math]. The boundary condition at the free surface ([math]\displaystyle{ z=0 \, }[/math]) gives rise to:
which is the Dispersion Relation for a Free Surface
The above equation is a transcendental equation. If we solve for all roots in the complex plane we find that the first root is a pair of imaginary roots. We denote the imaginary solutions of this equation by [math]\displaystyle{ k_{0}=\pm ik \, }[/math] and the positive real solutions by [math]\displaystyle{ k_{m} \, }[/math], [math]\displaystyle{ m\geq1 }[/math]. The [math]\displaystyle{ k \, }[/math] of the imaginary solution is the wavenumber. We put the imaginary roots back into the equation above and use the hyperbolic relations
[math]\displaystyle{ \cos ix = \cosh x, \quad \sin ix = i\sinh x, }[/math]
to arrive at the dispersion relation
[math]\displaystyle{ \alpha = k\tanh kh. }[/math]
We note that for a specified frequency [math]\displaystyle{ \omega \, }[/math] the equation determines the wavenumber [math]\displaystyle{ k \, }[/math].
Finally we define the function [math]\displaystyle{ Z(z) \, }[/math] as
[math]\displaystyle{ \chi_{m}\left( z\right) =\frac{\cos k_{m}(z+h)}{\cos k_{m}h},\quad m\geq0 }[/math]
as the vertical eigenfunction of the potential in the open water region. From Sturm-Liouville theory the vertical eigenfunctions are orthogonal. They can be normalised to be orthonormal, but this has no advantages for a numerical implementation. It can be shown that
[math]\displaystyle{ \int\nolimits_{-h}^{0}\chi_{m}(z)\chi_{n}(z) \mathrm{d} z=A_{n}\delta_{mn} }[/math]
where
[math]\displaystyle{ A_{n}=\frac{1}{2}\left( \frac{\cos k_{n}h\sin k_{n}h+k_{n}h}{k_{n}\cos ^{2}k_{n}h}\right). }[/math]
Separation of variables under the Plate
[math]\displaystyle{ Z^{\prime\prime} + \kappa^2 Z =0. }[/math]
subject to the boundary conditions
[math]\displaystyle{ Z^{\prime}(-h) = 0 }[/math]
and
[math]\displaystyle{ \left(\beta \kappa^4 + 1 - \alpha\gamma\right)Z^{\prime}(0) = \alpha Z(0) }[/math]
(the first term comes from the beam eigenvalue problem, where [math]\displaystyle{ \partial_x^4 X = \kappa^4 X }[/math]). We then use the boundary condition at [math]\displaystyle{ z=-h \, }[/math] to write
[math]\displaystyle{ Z = \frac{\cos \kappa(z+h)}{\cos \kappa h} }[/math]
The boundary condition at the free surface ([math]\displaystyle{ z=0 }[/math]) is the Dispersion Relation for a Floating Elastic Plate
Solving for [math]\displaystyle{ \kappa \, }[/math] gives a pure imaginary root with positive imaginary part, two complex roots (two complex conjugate paired roots with positive imaginary part in most physical situations), an infinite number of positive real roots which approach [math]\displaystyle{ {n\pi}/{h} \, }[/math] as [math]\displaystyle{ n }[/math] approaches infinity, and also the negative of all these roots (Dispersion Relation for a Floating Elastic Plate) . We denote the two complex roots with positive imaginary part by [math]\displaystyle{ \kappa_{-2} \, }[/math] and [math]\displaystyle{ \kappa_{-1} \, }[/math], the purely imaginary root with positive imaginary part by [math]\displaystyle{ \kappa_{0} \, }[/math] and the real roots with positive imaginary part by [math]\displaystyle{ \kappa_{n} \, }[/math] for [math]\displaystyle{ n }[/math] a positive integer. The imaginary root with positive imaginary part corresponds to a reflected travelling mode propagating along the [math]\displaystyle{ x }[/math] axis. The complex roots with positive imaginary parts correspond to damped reflected travelling modes and the real roots correspond to reflected evanescent modes.
Inner product between free surface and elastic plate modes
[math]\displaystyle{ \int\nolimits_{-h}^{0}\phi_{n}(z)\psi_{m}(z) d z=B_{mn} }[/math]
where
Incident potential
To create meaningful solutions of the velocity potential [math]\displaystyle{ \phi }[/math] in the specified domains we add an incident wave term to the expansion for the domain of [math]\displaystyle{ x \lt 0 }[/math] above. The incident potential is a wave of amplitude [math]\displaystyle{ A }[/math] in displacement travelling in the positive [math]\displaystyle{ x }[/math]-direction. We would only see this in the time domain [math]\displaystyle{ \Phi(x,z,t) }[/math] however, in the frequency domain the incident potential can be written as
[math]\displaystyle{ \phi_{\mathrm{I}}(x,z) =e^{-k_{0}x}\chi_{0}\left( z\right). }[/math]
The total velocity (scattered) potential now becomes [math]\displaystyle{ \phi = \phi_{\mathrm{I}} + \phi_{\mathrm{D}} }[/math] for the domain of [math]\displaystyle{ x \lt 0 }[/math].
The first term in the expansion of the diffracted potential for the domain [math]\displaystyle{ x \lt 0 }[/math] is given by
[math]\displaystyle{ a_{0}e^{k_{0}x}\chi_{0}\left( z\right) }[/math]
which represents the reflected wave.
In any scattering problem [math]\displaystyle{ |R|^2 + |T|^2 = 1 }[/math] where [math]\displaystyle{ R }[/math] and [math]\displaystyle{ T }[/math] are the reflection and transmission coefficients respectively. In our case of the semi-infinite dock [math]\displaystyle{ |a_{0}| = |R| = 1 }[/math] and [math]\displaystyle{ |T| = 0 }[/math] as there are no transmitted waves in the region under the dock.
An infinite dimensional system of equations
The potential and its derivative must be continuous across the transition from open water to the plate covered region. Therefore, the potentials and their derivatives at [math]\displaystyle{ x=0 }[/math] have to be equal. We also truncate the sum at [math]\displaystyle{ N }[/math] being careful that we have two extra modes on the plate covered region to satisfy the edge conditions. We obtain
[math]\displaystyle{ \phi_{0}\left( z\right) + \sum_{m=0}^{N} a_{m} \phi_{m}\left( z\right) =\sum_{m=-2}^{N}b_{m}\psi_{m}(z) }[/math]
and
[math]\displaystyle{ -k_{0}\phi_{0}\left( z\right) +\sum _{m=0}^{N} a_{m}k_{m}\phi_{m}\left( z\right) =-\sum_{m=-2}^{N}b_{m}\kappa_{m}\psi _{m}(z) }[/math]
for each [math]\displaystyle{ N }[/math]. We solve these equations by multiplying both equations by [math]\displaystyle{ \phi_{l}(z)\, }[/math] and integrating from [math]\displaystyle{ -h }[/math] to [math]\displaystyle{ 0 }[/math] to obtain:
[math]\displaystyle{ A_{0}\delta_{0l}+a_{l}A_{l} =\sum_{m=-2}^{N}b_{m}B_{ml},\,\,0 \leq l \leq N }[/math]
and
[math]\displaystyle{ -k_{0}A_{0}\delta_{0l}+a_{l}k_{l}A_l =-\sum_{m=-2}^{N}b_{m}\kappa_{m}B_{ml},\,\,0 \leq l \leq N }[/math]
If we multiply the first equation by [math]\displaystyle{ k_l }[/math] and subtract the second equation we obtain
[math]\displaystyle{ (k_{0}+k_l)A_{0}\delta_{0l} =\sum_{m=-2}^{N}b_{m}(k_l + \kappa_{m})B_{ml} }[/math]
Finally, we need to apply the conditions at the edge of the plate to give us two further equations,
[math]\displaystyle{ \partial_x^2\partial_z\phi = \sum_{m=-2}^{N}b_{m} \kappa_m^3 \tan\kappa_m h = 0 }[/math]
and
[math]\displaystyle{ \partial_x^3\partial_z\phi = - \sum_{m=-2}^{N}b_{m} \kappa_m^4 \tan\kappa_m h = 0 }[/math]
Numerical Solution
To solve the system of equations previously defined we set the upper limit of [math]\displaystyle{ l }[/math] to be [math]\displaystyle{ N }[/math], as stated before. In terms of matrix, we obtain
[math]\displaystyle{ \begin{bmatrix} \begin{bmatrix} A_0&0 \quad \cdots&0\\ 0&&\\ \vdots&A_l&\vdots\\ &&0\\ 0&\cdots \quad 0 &A_N \end{bmatrix} & \begin{bmatrix} -B_{-2,0}&-B_{-1,0}\\ &\\ \vdots&\vdots\\ &\\ -B_{-2,N}&-B_{-1,N} \end{bmatrix} & \begin{bmatrix} -B_{0,0}&\cdots&-B_{0,N}\\ &&\\ \vdots&-B_{m,l}&\vdots\\ &&\\ -B_{N,0}&\cdots&-B_{N,N} \end{bmatrix} \\ \\ \begin{bmatrix} 0&&\cdots&&0\\ 0&&\cdots&&0 \end{bmatrix} & \begin{bmatrix} \kappa_{-2}^3\tan\kappa_{-2}h&\kappa_{-1}^3\tan\kappa_{-1}h\\ \kappa_{-2}^4\tan\kappa_{-2}h&\kappa_{-1}^4\tan\kappa_{-1}h \end{bmatrix} & \begin{bmatrix} \kappa_0^3\tan\kappa_0h&\cdots&\kappa_N^3\tan\kappa_Nh\\ \kappa_0^4\tan\kappa_0h&\cdots&\kappa_N^4\tan\kappa_Nh \end{bmatrix} \\ \\ \begin{bmatrix} 0&&\cdots&&0\\ &&&&\\ \vdots&&\ddots&&\vdots\\ &&&&\\ 0&&\cdots&&0 \end{bmatrix} & \begin{bmatrix} (k_0+\kappa_{-2})B_{-2,0}&(k_0+\kappa_{-1})B_{-1,0}\\ &\\ \vdots&\vdots\\ &\\ (k_N+\kappa_{-2})B_{-2,N}&(k_N+\kappa_{-1})B_{-1,N} \end{bmatrix} & \begin{bmatrix} (k_0 + \kappa_0) \, B_{0,0}&\cdots&(k_N + \kappa_{0}) \, B_{0,N}\\ &&\\ \vdots&(k_l + \kappa_{m}) \, B_{m,l}&\vdots\\ &&\\ (k_0 + \kappa_N) \, B_{N,0}&\cdots&(k_N + \kappa_{N}) \, B_{N,N}\\ \end{bmatrix} \end{bmatrix} \begin{bmatrix} \begin{bmatrix} a_{0} \\ \\ \vdots \\ \\ a_N \end{bmatrix} \\ \\ \begin{bmatrix} b_{-2}\\ b_{-1} \end{bmatrix} \\ \\ \begin{bmatrix} b_{0}\\ \\ \vdots \\ \\ b_N \end{bmatrix} \end{bmatrix} = \begin{bmatrix} \begin{bmatrix} - A_{0} \\ 0 \\ \vdots \\ \\ 0 \end{bmatrix} \\ \\ \begin{bmatrix} 0 \\ 0 \end{bmatrix} \\ \\ \begin{bmatrix} 2k_{0}A_{0} \\ 0 \\ \vdots \\ \\ 0 \end{bmatrix} \end{bmatrix} }[/math]
We then simply need to solve the linear system of equations. Note that we can solve this equation for [math]\displaystyle{ b_n }[/math] first and then solve for [math]\displaystyle{ a_n }[/math]
Waves Incident at an Angle
We can consider the case of Waves Incident at an Angle [math]\displaystyle{ \theta }[/math]. When a wave in incident at an angle [math]\displaystyle{ \theta }[/math] we have the wavenumber in the [math]\displaystyle{ y }[/math] direction is [math]\displaystyle{ k_y = \sin\theta k_0 }[/math] where [math]\displaystyle{ k_0 }[/math] is as defined previously (note that [math]\displaystyle{ k_y }[/math] is imaginary).
This means that the potential is now of the form [math]\displaystyle{ \phi(x,y,z)=e^{k_y y}\phi(x,z) }[/math] so that when we separate variables we obtain
[math]\displaystyle{ k^2 = k_x^2 + k_y^2 }[/math]
where [math]\displaystyle{ k }[/math] is the separation constant calculated without an incident angle.
It is shown that the potential can be expanded as
[math]\displaystyle{ \phi(x,z)=e^{-\hat{k}_0x}\phi_0(z)+\sum_{m=0}^{\infty}a_{m}e^{\hat{k}_{m}x}\phi_{m}(z), \;\;x\lt 0 }[/math]
and
[math]\displaystyle{ \phi(x,z)=\sum_{m=-2}^{\infty}b_{m} e^{-\hat{\kappa}_{m}x}\psi_{m}(z), \;\;x\gt 0 }[/math]
where [math]\displaystyle{ \hat{k}_{m} = \sqrt{k_m^2 - k_y^2} }[/math] and [math]\displaystyle{ \hat{\kappa}_{m} = \sqrt{\kappa_m^2 - k_y^2} }[/math] where we always take the positive real root or the root with positive imaginary part.
The edge conditions are also different and are
and
where [math]\displaystyle{ \nu }[/math] is Poisons ratio.
We can expend these edge conditions, which respectively gives
[math]\displaystyle{ -\sum_{m=-2}^{\infty}b_{m}\kappa_m (\hat{\kappa}_m^3+\hat{\kappa}_m k_y^2(2-\nu))\tan \kappa_m h=0 }[/math]
and
[math]\displaystyle{ -\sum_{m=-2}^{\infty}b_{m}\kappa_m (\hat{\kappa}_m^2+k_y^2\nu))\tan \kappa_m h=0 }[/math]
The equations are derived almost identically to those above and we obtain
[math]\displaystyle{ A_{0}\delta_{0l}+a_{l}A_{l} =\sum_{m=-2}^{\infty}b_{m}B_{ml} }[/math]
and
[math]\displaystyle{ -\hat{k_{0}}A_{0}\delta_{0l}+a_{l}\hat{k}_{l}A_l =-\sum_{m=-2}^{\infty}b_{m}\hat{\kappa}_{m}B_{ml} }[/math]
and these are solved exactly as before.
Energy Balance
We present a derivation of the energy balance here and also refer to the derivation Energy Balance for Two Elastic Plates
Based on the method used in Evans and Davies 1968, a check can be made to ensure the solutions energy balance. The energy balance equation is derived by applying Green's theorem to [math]\displaystyle{ \phi }[/math] and its conjugate. The domain of integration is shown in the figure on the right. We assume that the angle is sufficiently small that we do not get total reflection.
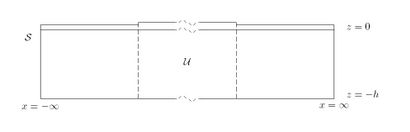
Applying Green's theorem to [math]\displaystyle{ \phi }[/math] and its conjugate [math]\displaystyle{ \phi^* }[/math] gives
where [math]\displaystyle{ n }[/math] denotes the outward plane normal to the boundary and [math]\displaystyle{ l }[/math] denotes the plane parallel to the boundary. As [math]\displaystyle{ \phi }[/math] and [math]\displaystyle{ \phi^* }[/math] satisfy the Laplace's equation, the left hand side of the Green theorem equation vanishes so that it reduces to
The contributions from the vertical ends are
and
The contribution from the surface integral under the plate is
where we have integrated by parts and used the condition at the ends of the plate.
The energy balance is therefore
Note that this formula is only valid for angles [math]\displaystyle{ \theta \in [-\theta_0, \theta_0] }[/math], where [math]\displaystyle{ \theta_0 }[/math]
is defined by [math]\displaystyle{ \sin \theta_0 =\frac{\kappa_0}{k_0} }[/math]. For large angles there is total reflection
and then [math]\displaystyle{ |R|^2=1 }[/math]
Matlab Code
A program to calculate the coefficients for the semi-infinite dock problems can be found here semiinfinite_plate.m
Additional code
This program requires