Difference between revisions of "Eigenfunction Matching for a Submerged Semi-Infinite Dock"
| (30 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | = Introduction = | + | {{complete pages}} |
| + | |||
| + | == Introduction == | ||
The problems consists of a region to the left | The problems consists of a region to the left | ||
| Line 7: | Line 9: | ||
We begin with the simply problem when the waves are normally incident (so that | We begin with the simply problem when the waves are normally incident (so that | ||
the problem is truly two-dimensional). We then consider the case when the waves are incident | the problem is truly two-dimensional). We then consider the case when the waves are incident | ||
| − | at an angle. For the later we refer to the solution [[Eigenfunction Matching for a Semi-Infinite Dock]] | + | at an angle. For the later we refer to the solution [[Eigenfunction Matching for a Semi-Infinite Dock]]. |
| + | The solution is a modified version of that given by [[Linton and Evans 1991]]. | ||
[[Image:submerged_inf_dock.jpg|thumb|right|300px|Wave scattering by a submerged semi-infinite dock]] | [[Image:submerged_inf_dock.jpg|thumb|right|300px|Wave scattering by a submerged semi-infinite dock]] | ||
| − | =Governing Equations= | + | == Governing Equations == |
We begin with the [[Frequency Domain Problem]] for the submerged dock in | We begin with the [[Frequency Domain Problem]] for the submerged dock in | ||
| Line 29: | Line 32: | ||
</math> | </math> | ||
</center> | </center> | ||
| − | <center><math> | + | <center> |
| + | <math> | ||
\partial_z\phi=\alpha\phi, \,\, z=0, | \partial_z\phi=\alpha\phi, \,\, z=0, | ||
| − | </math></center> | + | </math> |
| + | </center> | ||
<center> | <center> | ||
<math> | <math> | ||
| Line 43: | Line 48: | ||
and a wave propagating away. | and a wave propagating away. | ||
| − | =Solution Method= | + | == Solution Method == |
| − | We use [http://en.wikipedia.org/wiki/Separation_of_Variables separation of variables] in the three regions | + | We use [http://en.wikipedia.org/wiki/Separation_of_Variables separation of variables] in the three regions: {<math>x<0 \,</math>}, |
| − | <math>-d<z<0,\,\,x>0</math>, and <math>-h<z<-d,\,\,x>0</math>. The first two regions use the free-surface eigenfunction | + | {<math>-d<z<0,\,\,x>0</math> }, and {<math>-h<z<-d,\,\,x>0</math> }. The first two regions use the free-surface eigenfunction |
| − | and the third uses the dock eigenfunctions | + | and the third uses the dock eigenfunctions. |
| − | + | {{separation of variables in two dimensions}} | |
| − | in | + | |
| − | + | {{separation of variables for a free surface}} | |
| − | + | ||
| − | + | {{separation of variables for a dock}} | |
| − | + | We now adjust for the fact that the dock is submerged. | |
| − | + | {{separation of variables for a submerged dock}} | |
| − | + | ||
| − | + | {{free surface submerged plate relations}} | |
| + | |||
| + | === Expansion of the potential === | ||
| + | |||
| + | We need to apply some boundary conditions at plus and minus infinity, | ||
| + | where are essentially that the solution cannot grow. This means that we | ||
| + | only have the positive (or negative) roots of the dispersion equation. | ||
| + | However, it does not help us with the purely imaginary root. Here we | ||
| + | must use a different condition, essentially identifying one solution | ||
| + | as the incoming wave and the other as the outgoing wave. | ||
| − | + | Therefore the potential (without the incident wave, which will | |
| + | be added later) can | ||
be expanded as | be expanded as | ||
<center> | <center> | ||
<math> | <math> | ||
| − | \phi(x,z)= | + | \phi(x,z)=\sum_{m=0}^{\infty}a_{m}e^{k_{m}^{h}x}\phi_{m}^{h}(z), \;\;x<0 |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
</math> | </math> | ||
</center> | </center> | ||
| Line 77: | Line 84: | ||
<center> | <center> | ||
<math> | <math> | ||
| − | \phi(x,z)= \sum_{m=0}^{\infty} | + | \phi(x,z)=\sum_{m=0}^{\infty}b_{m} |
| − | e^{\ | + | e^{-\mu_{m}x}\chi_{m}(z), \;\;x>0 |
| − | , \;\; | ||
</math> | </math> | ||
</center> | </center> | ||
where <math>a_{m}</math> and <math>b_{m}</math> | where <math>a_{m}</math> and <math>b_{m}</math> | ||
| − | are the coefficients of the potential in the open water | + | are the coefficients of the potential in the open water and |
| − | + | the dock covered region respectively. | |
| − | covered region | + | |
| − | + | {{incident potential for two dimensions}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ==An infinite dimensional system of equations== | + | === An infinite dimensional system of equations === |
The potential and its derivative must be continuous across the | The potential and its derivative must be continuous across the | ||
| − | transition from open water to the | + | transition from open water to the plate covered region. Therefore, the |
potentials and their derivatives at <math>x=0</math> have to be equal. | potentials and their derivatives at <math>x=0</math> have to be equal. | ||
We obtain | We obtain | ||
<center> | <center> | ||
<math> | <math> | ||
| − | \phi_{0} | + | \phi_{0}\left( z\right) + \sum_{m=0}^{\infty} |
| − | a_{m} \phi_{m}^h\left( z\right) | + | a_{m} \phi_{m}^{h}\left( z\right) |
| − | =\sum_{m=0}^{\infty}b_{m}\ | + | =\sum_{m=0}^{\infty}b_{m}\chi_{m}(z) |
</math> | </math> | ||
</center> | </center> | ||
| + | and | ||
<center> | <center> | ||
<math> | <math> | ||
| − | \phi_{0} | + | -k_{0}^{h}\phi_{0}\left( z\right) +\sum |
| − | a_{m} \phi_{m}^h\left( z\right) | + | _{m=0}^{\infty} a_{m}k_{m}^{h}\phi_{m}^{h}\left( z\right) |
| − | =\sum_{m=0}^{\infty} | + | =-\sum_{m=0}^{\infty}b_{m}\mu_{m}\chi |
| + | _{m}(z) | ||
</math> | </math> | ||
</center> | </center> | ||
| + | for each <math>n</math>. | ||
| + | We solve these equations by multiplying both equations by | ||
| + | <math> \phi_{l}^{h}(z) \,</math> and integrating from <math>-h</math> to <math>0</math> to obtain: | ||
<center> | <center> | ||
<math> | <math> | ||
| − | + | A_{0}\delta_{0l}+a_{l}A_{l} | |
| − | + | =\sum_{n=0}^{\infty}b_{m}B_{ml} | |
| − | =\sum_{ | ||
</math> | </math> | ||
</center> | </center> | ||
| + | and | ||
<center> | <center> | ||
<math> | <math> | ||
| − | - | + | -k_{0}^{h}A_{0}\delta_{0l}+a_{l}k_{l}^{h}A_l |
| − | + | =-\sum_{m=0}^{\infty}b_{m}\mu_{m}B_{ml} | |
| − | =\sum_{m=0}^{\infty} | ||
</math> | </math> | ||
</center> | </center> | ||
| + | We solve these equations in the standard way by truncation. | ||
| + | |||
| + | == Solution with Waves Incident at an Angle == | ||
| − | + | We can consider the problem when the waves are incident at an angle <math>\theta</math>. | |
| − | + | {{incident angle}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Therefore the potential can | |
| + | be expanded as | ||
<center> | <center> | ||
<math> | <math> | ||
| − | \ | + | \phi(x,z)=e^{-\hat{k}_0x}\phi_0(z)+\sum_{m=0}^{\infty}a_{m}e^{\hat{k}_{m}x}\phi_{m}(z), \;\;x<0 |
| − | \ | ||
| − | \ | ||
| − | |||
| − | |||
</math> | </math> | ||
</center> | </center> | ||
| − | + | and | |
<center> | <center> | ||
<math> | <math> | ||
| − | \ | + | \phi(x,z)=\sum_{m=0}^{\infty}b_{m} |
| − | \ | + | e^{-\hat{\mu}_{m}x}\chi_{m}(z), \;\;x>0 |
| − | |||
| − | |||
| − | |||
</math> | </math> | ||
</center> | </center> | ||
| − | + | where <math>\hat{k}_{m} = \sqrt{k_m^2 - k_y^2}</math> and <math>\hat{\mu}_{m} = \sqrt{\mu_m^2 - k_y^2}</math> | |
| − | and | + | where we always take the positive real root or the root with positive imaginary part. |
| − | |||
| − | |||
| − | |||
| + | The equations are derived almost identically to those above and we obtain | ||
<center> | <center> | ||
<math> | <math> | ||
| − | + | A_{0}\delta_{0l}+a_{l}A_{l} | |
| − | a_{ | + | =\sum_{n=0}^{\infty}b_{m}B_{ml} |
| − | =\sum_{ | ||
</math> | </math> | ||
</center> | </center> | ||
| + | and | ||
<center> | <center> | ||
<math> | <math> | ||
| − | - | + | -\hat{k_{0}}A_{0}\delta_{0l}+a_{l}\hat{k}_{l}A_l |
| − | + | =-\sum_{m=0}^{\infty}b_{m}\hat{\mu}_{m}B_{ml} | |
| − | =\sum_{m=0} | ||
</math> | </math> | ||
</center> | </center> | ||
| − | + | and these are solved exactly as before. | |
| − | as | ||
| − | + | == Energy Balance == | |
| − | + | ||
| − | + | {{energy contour and preliminaries}} | |
| − | |||
| − | |||
| − | = | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | = | ||
| − | |||
| − | |||
| − | |||
| − | + | We only get contributions from the vertical ends and we obtain | |
| − | + | <center><math> | |
| − | is | + | \lim_{x\to-\infty} \Im\int_{-h}^{0}\phi^*\frac{\partial\phi}{\partial n} \mathrm{d}z |
| + | = \lim_{x\to-\infty} \Im\int_{-h}^{0} \hat{k}_0 \left(e^{\hat{k}_0 x} + a_0^{*} e^{-\hat{k}_0 x} \right) | ||
| + | \left(e^{-\hat{k}_0 x} - a_0 e^{\hat{k}_0 x} \right)\phi_0(z)^2 \mathrm{d}z | ||
| + | </math></center> | ||
| + | <center><math> | ||
| + | = \frac{\hat{k}_0}{i} A_0 \left(1 - |a_0^2| \right) | ||
| + | </math></center> | ||
| + | and | ||
| + | <center><math> | ||
| + | \lim_{x\to\infty} \Im\int_{-h}^{0}\phi^*\frac{\partial\phi}{\partial n} \mathrm{d}z | ||
| + | = \lim_{x\to\infty} \Im\int_{-h}^{0} -\hat{\mu}_0 \left(b_0^{*} e^{\hat{\mu}_0 x} \right) | ||
| + | \left(b_0 e^{-\hat{\mu}_0 x}\right)\chi_0(z)^2 \mathrm{d}z | ||
| + | </math></center> | ||
| + | <center><math> | ||
| + | = - \frac{\hat{\mu}_0}{i} |b_0^2| \int_{-h}^{0} \chi_0(z)^2 \mathrm{d}z | ||
| + | </math></center> | ||
| + | Therefore the energy balance can be written as | ||
| + | <center><math> | ||
| + | \hat{k}_0 A_0 |a_0^2| + \hat{\mu}_0 |b_0^2| \int_{-h}^{0} \chi_0(z)^2 \mathrm{d}z = \hat{k}_0 A_0 | ||
| + | </math></center> | ||
| + | Note that the second integral above is actually only from <math>-d</math> to 0. | ||
| − | = Matlab Code = | + | == Matlab Code == |
A program to calculate the coefficients for the submerged semi-infinite dock problems can be found here | A program to calculate the coefficients for the submerged semi-infinite dock problems can be found here | ||
[http://www.math.auckland.ac.nz/~meylan/code/eigenfunction_matching/submerged_semiinfinite_dock.m submerged_semiinfinite_dock.m] | [http://www.math.auckland.ac.nz/~meylan/code/eigenfunction_matching/submerged_semiinfinite_dock.m submerged_semiinfinite_dock.m] | ||
| − | == Additional code == | + | === Additional code === |
This program requires | This program requires | ||
| − | + | * {{free surface dispersion equation code}} | |
| − | + | ||
[[Category:Eigenfunction Matching Method]] | [[Category:Eigenfunction Matching Method]] | ||
[[Category:Pages with Matlab Code]] | [[Category:Pages with Matlab Code]] | ||
| + | [[Category:Complete Pages]] | ||
Latest revision as of 23:59, 16 October 2009
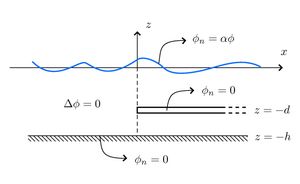
Introduction
The problems consists of a region to the left with a free surface and a region to the right with a free surface and a submerged dock/plate through which not flow is possible. We begin with the simply problem when the waves are normally incident (so that the problem is truly two-dimensional). We then consider the case when the waves are incident at an angle. For the later we refer to the solution Eigenfunction Matching for a Semi-Infinite Dock. The solution is a modified version of that given by Linton and Evans 1991.
Governing Equations
We begin with the Frequency Domain Problem for the submerged dock in the region [math]\displaystyle{ x\gt 0 }[/math] (we assume [math]\displaystyle{ e^{i\omega t} }[/math] time dependence). The water is assumed to have constant finite depth [math]\displaystyle{ h }[/math] and the [math]\displaystyle{ z }[/math]-direction points vertically upward with the water surface at [math]\displaystyle{ z=0 }[/math] and the sea floor at [math]\displaystyle{ z=-h }[/math]. The boundary value problem can therefore be expressed as
[math]\displaystyle{ \Delta\phi=0, \,\, -h\lt z\lt 0, }[/math]
[math]\displaystyle{ \phi_{z}=0, \,\, z=-h, }[/math]
[math]\displaystyle{ \partial_z\phi=\alpha\phi, \,\, z=0, }[/math]
[math]\displaystyle{ \partial_z\phi=0, \,\, z=-d,\,x\gt 0, }[/math]
We must also apply the Sommerfeld Radiation Condition as [math]\displaystyle{ |x|\rightarrow\infty }[/math]. This essentially implies that the only wave at infinity is propagating away and at negative infinity there is a unit incident wave and a wave propagating away.
Solution Method
We use separation of variables in the three regions: {[math]\displaystyle{ x\lt 0 \, }[/math]}, {[math]\displaystyle{ -d\lt z\lt 0,\,\,x\gt 0 }[/math] }, and {[math]\displaystyle{ -h\lt z\lt -d,\,\,x\gt 0 }[/math] }. The first two regions use the free-surface eigenfunction and the third uses the dock eigenfunctions.
We express the potential as
[math]\displaystyle{ \phi(x,z) = X(x)Z(z)\, }[/math]
and then Laplace's equation becomes
[math]\displaystyle{ \frac{X^{\prime\prime}}{X} = - \frac{Z^{\prime\prime}}{Z} = k^2 }[/math]
Separation of variables for a free surface
We use separation of variables
We express the potential as
[math]\displaystyle{ \phi(x,z) = X(x)Z(z)\, }[/math]
and then Laplace's equation becomes
[math]\displaystyle{ \frac{X^{\prime\prime}}{X} = - \frac{Z^{\prime\prime}}{Z} = k^2 }[/math]
The separation of variables equation for deriving free surface eigenfunctions is as follows:
[math]\displaystyle{ Z^{\prime\prime} + k^2 Z =0. }[/math]
subject to the boundary conditions
[math]\displaystyle{ Z^{\prime}(-h) = 0 }[/math]
and
[math]\displaystyle{ Z^{\prime}(0) = \alpha Z(0) }[/math]
We can then use the boundary condition at [math]\displaystyle{ z=-h \, }[/math] to write
[math]\displaystyle{ Z = \frac{\cos k(z+h)}{\cos kh} }[/math]
where we have chosen the value of the coefficent so we have unit value at [math]\displaystyle{ z=0 }[/math]. The boundary condition at the free surface ([math]\displaystyle{ z=0 \, }[/math]) gives rise to:
which is the Dispersion Relation for a Free Surface
The above equation is a transcendental equation. If we solve for all roots in the complex plane we find that the first root is a pair of imaginary roots. We denote the imaginary solutions of this equation by [math]\displaystyle{ k_{0}=\pm ik \, }[/math] and the positive real solutions by [math]\displaystyle{ k_{m} \, }[/math], [math]\displaystyle{ m\geq1 }[/math]. The [math]\displaystyle{ k \, }[/math] of the imaginary solution is the wavenumber. We put the imaginary roots back into the equation above and use the hyperbolic relations
[math]\displaystyle{ \cos ix = \cosh x, \quad \sin ix = i\sinh x, }[/math]
to arrive at the dispersion relation
[math]\displaystyle{ \alpha = k\tanh kh. }[/math]
We note that for a specified frequency [math]\displaystyle{ \omega \, }[/math] the equation determines the wavenumber [math]\displaystyle{ k \, }[/math].
Finally we define the function [math]\displaystyle{ Z(z) \, }[/math] as
[math]\displaystyle{ \chi_{m}\left( z\right) =\frac{\cos k_{m}(z+h)}{\cos k_{m}h},\quad m\geq0 }[/math]
as the vertical eigenfunction of the potential in the open water region. From Sturm-Liouville theory the vertical eigenfunctions are orthogonal. They can be normalised to be orthonormal, but this has no advantages for a numerical implementation. It can be shown that
[math]\displaystyle{ \int\nolimits_{-h}^{0}\chi_{m}(z)\chi_{n}(z) \mathrm{d} z=A_{n}\delta_{mn} }[/math]
where
[math]\displaystyle{ A_{n}=\frac{1}{2}\left( \frac{\cos k_{n}h\sin k_{n}h+k_{n}h}{k_{n}\cos ^{2}k_{n}h}\right). }[/math]
Separation of Variables for a Dock
The separation of variables equation for a floating dock
[math]\displaystyle{ Z^{\prime\prime} + k^2 Z =0, }[/math]
subject to the boundary conditions
[math]\displaystyle{ Z^{\prime} (-h) = 0, }[/math]
and
[math]\displaystyle{ Z^{\prime} (0) = 0. }[/math]
The solution is [math]\displaystyle{ k=\kappa_{m}= \frac{m\pi}{h} \, }[/math], [math]\displaystyle{ m\geq 0 }[/math] and
[math]\displaystyle{ Z = \psi_{m}\left( z\right) = \cos\kappa_{m}(z+h),\quad m\geq 0. }[/math]
We note that
[math]\displaystyle{ \int\nolimits_{-h}^{0}\psi_{m}(z)\psi_{n}(z) \mathrm{d} z=C_{m}\delta_{mn}, }[/math]
where
[math]\displaystyle{ C_{m} = \begin{cases} h,\quad m=0 \\ \frac{1}{2}h,\,\,\,m\neq 0 \end{cases} }[/math]
We now adjust for the fact that the dock is submerged. The depth above the plate is [math]\displaystyle{ d }[/math] and below the plate is [math]\displaystyle{ h-d }[/math]. We introduce a new dispersion value [math]\displaystyle{ \mu_n }[/math]:
[math]\displaystyle{ \mu_n = \begin{cases} k_n^{d},\qquad \qquad\mbox{for}\,\, 0 \leq n \leq N-M\\ n\pi/(h-d),\,\,\mbox{otherwise} \end{cases} }[/math]
where [math]\displaystyle{ k_n^{d} }[/math] are the roots of the Dispersion Relation for a Free Surface with depth [math]\displaystyle{ d }[/math]. We also order the roots with the first being the positive imaginary solution [math]\displaystyle{ k_0^{d} }[/math], the second being zero, then ordering by increasing size. We then define a new function
[math]\displaystyle{ \chi_n = \begin{cases} 0,\,\,\, \qquad-d\lt z\lt 0 \\ \psi_{n}(z),\,\,\,-h\lt z\lt -d \end{cases} }[/math]
or
[math]\displaystyle{ \chi_{n} = \begin{cases} \phi_{n}^{d}(z),\,\,\,-d\lt z\lt 0 \\ 0,\,\,\qquad-h\lt z\lt -d \end{cases} }[/math]
where
[math]\displaystyle{ \phi_{m}^{d}\left( z\right) =\frac{\cos k_{m}^{d}(z+d)}{\cos k_{m}^{d}d},\quad m\geq0 }[/math]
depending on whether the root [math]\displaystyle{ \mu_n }[/math] is above or below.
Inner product between free surface and submerged plate modes
We define
[math]\displaystyle{ \int\nolimits_{-d}^{0}\phi_{n}^h(z)\chi_{m}^d(z) \mathrm{d} z=B_{mn} }[/math]
where [math]\displaystyle{ B_{mn} }[/math] is either
[math]\displaystyle{ \int\nolimits_{-d}^{0}\phi_{n}^h(z)\phi_{m}^d(z) \mathrm{d} z }[/math]
or
[math]\displaystyle{ \int\nolimits_{-h}^{-d}\phi_{n}^h(z)\psi_{m}(z) \mathrm{d} z }[/math]
depending on whether the root [math]\displaystyle{ \mu_n }[/math] is above or below.
Expansion of the potential
We need to apply some boundary conditions at plus and minus infinity, where are essentially that the solution cannot grow. This means that we only have the positive (or negative) roots of the dispersion equation. However, it does not help us with the purely imaginary root. Here we must use a different condition, essentially identifying one solution as the incoming wave and the other as the outgoing wave.
Therefore the potential (without the incident wave, which will be added later) can be expanded as
[math]\displaystyle{ \phi(x,z)=\sum_{m=0}^{\infty}a_{m}e^{k_{m}^{h}x}\phi_{m}^{h}(z), \;\;x\lt 0 }[/math]
and
[math]\displaystyle{ \phi(x,z)=\sum_{m=0}^{\infty}b_{m} e^{-\mu_{m}x}\chi_{m}(z), \;\;x\gt 0 }[/math]
where [math]\displaystyle{ a_{m} }[/math] and [math]\displaystyle{ b_{m} }[/math] are the coefficients of the potential in the open water and the dock covered region respectively.
Incident potential
To create meaningful solutions of the velocity potential [math]\displaystyle{ \phi }[/math] in the specified domains we add an incident wave term to the expansion for the domain of [math]\displaystyle{ x \lt 0 }[/math] above. The incident potential is a wave of amplitude [math]\displaystyle{ A }[/math] in displacement travelling in the positive [math]\displaystyle{ x }[/math]-direction. We would only see this in the time domain [math]\displaystyle{ \Phi(x,z,t) }[/math] however, in the frequency domain the incident potential can be written as
[math]\displaystyle{ \phi_{\mathrm{I}}(x,z) =e^{-k_{0}x}\chi_{0}\left( z\right). }[/math]
The total velocity (scattered) potential now becomes [math]\displaystyle{ \phi = \phi_{\mathrm{I}} + \phi_{\mathrm{D}} }[/math] for the domain of [math]\displaystyle{ x \lt 0 }[/math].
The first term in the expansion of the diffracted potential for the domain [math]\displaystyle{ x \lt 0 }[/math] is given by
[math]\displaystyle{ a_{0}e^{k_{0}x}\chi_{0}\left( z\right) }[/math]
which represents the reflected wave.
In any scattering problem [math]\displaystyle{ |R|^2 + |T|^2 = 1 }[/math] where [math]\displaystyle{ R }[/math] and [math]\displaystyle{ T }[/math] are the reflection and transmission coefficients respectively. In our case of the semi-infinite dock [math]\displaystyle{ |a_{0}| = |R| = 1 }[/math] and [math]\displaystyle{ |T| = 0 }[/math] as there are no transmitted waves in the region under the dock.
An infinite dimensional system of equations
The potential and its derivative must be continuous across the transition from open water to the plate covered region. Therefore, the potentials and their derivatives at [math]\displaystyle{ x=0 }[/math] have to be equal. We obtain
[math]\displaystyle{ \phi_{0}\left( z\right) + \sum_{m=0}^{\infty} a_{m} \phi_{m}^{h}\left( z\right) =\sum_{m=0}^{\infty}b_{m}\chi_{m}(z) }[/math]
and
[math]\displaystyle{ -k_{0}^{h}\phi_{0}\left( z\right) +\sum _{m=0}^{\infty} a_{m}k_{m}^{h}\phi_{m}^{h}\left( z\right) =-\sum_{m=0}^{\infty}b_{m}\mu_{m}\chi _{m}(z) }[/math]
for each [math]\displaystyle{ n }[/math]. We solve these equations by multiplying both equations by [math]\displaystyle{ \phi_{l}^{h}(z) \, }[/math] and integrating from [math]\displaystyle{ -h }[/math] to [math]\displaystyle{ 0 }[/math] to obtain:
[math]\displaystyle{ A_{0}\delta_{0l}+a_{l}A_{l} =\sum_{n=0}^{\infty}b_{m}B_{ml} }[/math]
and
[math]\displaystyle{ -k_{0}^{h}A_{0}\delta_{0l}+a_{l}k_{l}^{h}A_l =-\sum_{m=0}^{\infty}b_{m}\mu_{m}B_{ml} }[/math]
We solve these equations in the standard way by truncation.
Solution with Waves Incident at an Angle
We can consider the problem when the waves are incident at an angle [math]\displaystyle{ \theta }[/math].
When a wave in incident at an angle [math]\displaystyle{ \theta }[/math] we have the wavenumber in the [math]\displaystyle{ y }[/math] direction is [math]\displaystyle{ k_y = \sin\theta k_0 }[/math] where [math]\displaystyle{ k_0 }[/math] is as defined previously (note that [math]\displaystyle{ k_y }[/math] is imaginary).
This means that the potential is now of the form [math]\displaystyle{ \phi(x,y,z)=e^{k_y y}\phi(x,z) }[/math] so that when we separate variables we obtain
[math]\displaystyle{ k^2 = k_x^2 + k_y^2 }[/math]
where [math]\displaystyle{ k }[/math] is the separation constant calculated without an incident angle.
Therefore the potential can be expanded as
[math]\displaystyle{ \phi(x,z)=e^{-\hat{k}_0x}\phi_0(z)+\sum_{m=0}^{\infty}a_{m}e^{\hat{k}_{m}x}\phi_{m}(z), \;\;x\lt 0 }[/math]
and
[math]\displaystyle{ \phi(x,z)=\sum_{m=0}^{\infty}b_{m} e^{-\hat{\mu}_{m}x}\chi_{m}(z), \;\;x\gt 0 }[/math]
where [math]\displaystyle{ \hat{k}_{m} = \sqrt{k_m^2 - k_y^2} }[/math] and [math]\displaystyle{ \hat{\mu}_{m} = \sqrt{\mu_m^2 - k_y^2} }[/math] where we always take the positive real root or the root with positive imaginary part.
The equations are derived almost identically to those above and we obtain
[math]\displaystyle{ A_{0}\delta_{0l}+a_{l}A_{l} =\sum_{n=0}^{\infty}b_{m}B_{ml} }[/math]
and
[math]\displaystyle{ -\hat{k_{0}}A_{0}\delta_{0l}+a_{l}\hat{k}_{l}A_l =-\sum_{m=0}^{\infty}b_{m}\hat{\mu}_{m}B_{ml} }[/math]
and these are solved exactly as before.
Energy Balance
Based on the method used in Evans and Davies 1968, a check can be made to ensure the solutions energy balance. The energy balance equation is derived by applying Green's theorem to [math]\displaystyle{ \phi }[/math] and its conjugate. The domain of integration is shown in the figure on the right. We assume that the angle is sufficiently small that we do not get total reflection.
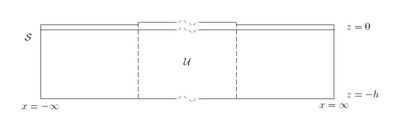
Applying Green's theorem to [math]\displaystyle{ \phi }[/math] and its conjugate [math]\displaystyle{ \phi^* }[/math] gives
where [math]\displaystyle{ n }[/math] denotes the outward plane normal to the boundary and [math]\displaystyle{ l }[/math] denotes the plane parallel to the boundary. As [math]\displaystyle{ \phi }[/math] and [math]\displaystyle{ \phi^* }[/math] satisfy the Laplace's equation, the left hand side of the Green theorem equation vanishes so that it reduces to
We only get contributions from the vertical ends and we obtain
and
Therefore the energy balance can be written as
Note that the second integral above is actually only from [math]\displaystyle{ -d }[/math] to 0.
Matlab Code
A program to calculate the coefficients for the submerged semi-infinite dock problems can be found here submerged_semiinfinite_dock.m
Additional code
This program requires