Difference between revisions of "Generalized Eigenfunction Expansion for Water Waves for a Fixed Body"
| (47 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | {{complete pages}} | |
| − | + | == Introduction == | |
| − | + | ||
| − | + | The generalized eigenfunction method goes back to | |
| − | + | the work of [[Povzner 1953]] and [[Ikebe 1960]]. The generalized eigenfunction | |
| − | |||
| − | the work of [[ | ||
method has been applied to water-wave problems by | method has been applied to water-wave problems by | ||
| − | + | [[Friedman and Shinbrot 1967]], [[Hazard_Lenoir2002a | Hazard and Lenoir 2002]] | |
| − | + | (for the case of a rigid body in water of infinite depth) | |
| − | + | and [[Meylan 2002b| Meylan 2002 ]] (for | |
| − | + | a thin plate on water of shallow draft). We will present here the theory for a rigid body | |
| − | + | in water of finite depth. | |
| − | + | rms of this solutions (which we call the generalised | |
| − | + | eigenfunctions) because they solve for | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | solutions | ||
| − | |||
| − | |||
| − | |||
| − | |||
The generalized eigenfunction method is based on an inner product in | The generalized eigenfunction method is based on an inner product in | ||
| Line 37: | Line 23: | ||
this is done, we can derive simple expressions which allow the | this is done, we can derive simple expressions which allow the | ||
time-domain problem to be solved in terms of the single-frequency | time-domain problem to be solved in terms of the single-frequency | ||
| − | solutions. The mathematical ideas | + | solutions. The mathematical ideas are discussed in detail in |
| − | + | [[Hazard and Loret 2007]]. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {{Equations for fixed bodies in the time domain}} | |
| − | + | == Equations in the Frequency Domain == | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {{frequency definition}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {{velocity potential in frequency domain}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | The equations are the following | |
| − | |||
| − | |||
| − | + | {{standard linear wave scattering equations without body condition}} | |
| − | + | {{frequency domain equations for a rigid body}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {{incident plane wave}} | |
| − | + | {{sommerfeld radiation condition two dimensions}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | == Time domain calculations == | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | =Time domain calculations= | ||
The solution in the frequency domain can be used to construct the | The solution in the frequency domain can be used to construct the | ||
| Line 210: | Line 56: | ||
transform. | transform. | ||
| − | + | We begin with the equations in the time domain subject to the initial conditions given by | |
| − | + | Denoting the potential at the surface by | |
| − | We begin with the equations in the time domain | ||
| − | |||
| − | |||
<center><math> | <center><math> | ||
| − | \ | + | \psi(x,t)=\left.\Phi\left(\mathbf{x},t\right)\right|_{z=0}, |
</math></center> | </math></center> | ||
we introduce the operator <math>\mathbf{G}</math> which maps the surface | we introduce the operator <math>\mathbf{G}</math> which maps the surface | ||
potential to the potential throughout the fluid domain. The operator | potential to the potential throughout the fluid domain. The operator | ||
<math>\mathbf{G}\psi</math> is found by solving | <math>\mathbf{G}\psi</math> is found by solving | ||
| − | |||
<center><math>\begin{matrix} | <center><math>\begin{matrix} | ||
\Delta\Psi\left( \mathbf{x}\right) & = 0,\ \ \mathbf{x}\in\Omega,\\ | \Delta\Psi\left( \mathbf{x}\right) & = 0,\ \ \mathbf{x}\in\Omega,\\ | ||
| Line 228: | Line 70: | ||
\Psi & =\psi,\ \ z = 0,\ x\in F, | \Psi & =\psi,\ \ z = 0,\ x\in F, | ||
\end{matrix}</math></center> | \end{matrix}</math></center> | ||
| − | + | and is defined by <math>\mathbf{G}\psi=\Psi.</math> The operator | |
| − | and is defined by <math>\mathbf{G}\psi=\Psi.</math> The operator < | + | <math>\partial_{n}\mathbf{G}</math>, which maps the surface potential to the normal |
| − | |||
derivative of potential at the surface (called the | derivative of potential at the surface (called the | ||
Dirichlet-to-Neumann map) is given by | Dirichlet-to-Neumann map) is given by | ||
| Line 236: | Line 77: | ||
\partial_{n}\mathbf{G}\psi=\left. \partial_{n}\Psi\right\vert _{z=0}. | \partial_{n}\mathbf{G}\psi=\left. \partial_{n}\Psi\right\vert _{z=0}. | ||
</math></center> | </math></center> | ||
| − | Therefore equations | + | Therefore the equations in the time domain can be written as |
| − | can be written as | ||
<center><math> | <center><math> | ||
\partial_{t}^2 \zeta + \partial_{n}\mathbf{G} \zeta = 0. | \partial_{t}^2 \zeta + \partial_{n}\mathbf{G} \zeta = 0. | ||
| Line 247: | Line 87: | ||
\left\langle \zeta,\eta \right\rangle _{\mathcal{H}}= | \left\langle \zeta,\eta \right\rangle _{\mathcal{H}}= | ||
\int_{F}\zeta \eta ^{*}\,\mathrm{d} x, | \int_{F}\zeta \eta ^{*}\,\mathrm{d} x, | ||
| − | |||
</math></center> | </math></center> | ||
| − | where <math> | + | where <math> *</math> denotes complex conjugate, and we assume that this |
symmetry implies that the operator is self-adjoint. We can prove the | symmetry implies that the operator is self-adjoint. We can prove the | ||
symmetry by using Green's second identity | symmetry by using Green's second identity | ||
| Line 266: | Line 105: | ||
<math>\zeta</math> and <math>\eta</math> respectively. | <math>\zeta</math> and <math>\eta</math> respectively. | ||
| − | + | == Eigenfunctions of <math>\partial_{n}\mathbf{G}</math> == | |
| − | ==Eigenfunctions of <math>\partial_{n | ||
The eigenfunctions of <math> \partial_{n}\mathbf{G}</math> satisfy | The eigenfunctions of <math> \partial_{n}\mathbf{G}</math> satisfy | ||
<center><math> | <center><math> | ||
\partial_{n}\mathbf{G} \zeta = \omega^2 \zeta. | \partial_{n}\mathbf{G} \zeta = \omega^2 \zeta. | ||
| − | |||
</math></center> | </math></center> | ||
| − | + | ||
| − | + | To solve | |
for the eigenfunctions of <math>\partial_{n}\mathbf{G}</math> we need to solve | for the eigenfunctions of <math>\partial_{n}\mathbf{G}</math> we need to solve | ||
the frequency-domain equations, and the radian frequency <math>\omega</math> is exactly | the frequency-domain equations, and the radian frequency <math>\omega</math> is exactly | ||
| Line 283: | Line 120: | ||
incident from the left and from the right). It is possible for there | incident from the left and from the right). It is possible for there | ||
to exist point spectra for this operator which correspond to the | to exist point spectra for this operator which correspond to the | ||
| − | existence of a trapped mode [[ | + | existence of a [[Trapped Modes|trapped mode]] [[McIver 1996]] |
| − | + | and the presence of a trapped mode requires that | |
| − | the generalized eigenfunction expansion we derive must be modified. | + | the generalized eigenfunction expansion we derive must be modified. |
| − | |||
==Normalization of the Eigenfunctions== | ==Normalization of the Eigenfunctions== | ||
The eigenfunctions of <math>\partial_{n}\mathbf{G}</math> (with eigenvalue | The eigenfunctions of <math>\partial_{n}\mathbf{G}</math> (with eigenvalue | ||
| − | <math>\omega</math>) are denoted by <math> \zeta_{\kappa}(x,k\left( \omega\right) ) </math>. | + | <math>\omega</math>) are denoted by <math> \zeta_{\kappa}(x,k\left( \omega\right) ) </math>, |
| + | where <math>\kappa = \pm 1</math> for waves incident from the left or right respectively. | ||
| + | We must also specify radiations conditions to normalize the eigenfunctions and they are given | ||
| + | by | ||
| + | <center><math> | ||
| + | {\zeta}_1 = \left( | ||
| + | \mathrm{e}^{\mathrm{i} kx} + R_1 e^{- \mathrm{i} k x} \right)\frac{\cos k_0\left( z+h\right) | ||
| + | }{\cos k_0h}, | ||
| + | \,\,\,\mathrm{as}\,\,x\to-\infty, | ||
| + | </math></center> | ||
| + | <center><math> | ||
| + | {\zeta}_1= | ||
| + | T_1\mathrm{e}^{\mathrm{i} k x}\frac{\cos k_0\left( z+h\right) }{\cos k_0h}, | ||
| + | \,\,\,\mathrm{as}\,\,x\to\infty, | ||
| + | </math></center> | ||
| + | <center><math> | ||
| + | {\zeta}_{-1} = | ||
| + | T_{-1}\mathrm{e}^{-\mathrm{i} k x} | ||
| + | \frac{\cos k_0\left( z+h\right) }{\cos k_0h}, | ||
| + | \,\,\,\mathrm{as}\,\,x\to\infty, | ||
| + | </math></center> | ||
| + | <center><math> | ||
| + | {\zeta}_{-1}= | ||
| + | \left( | ||
| + | \mathrm{e}^{-\mathrm{i} k x} + R_{-1} e^{\mathrm{i} k x} \right)\frac{\cos k_0\left( z+h\right) | ||
| + | }{\cos k_0 h}, | ||
| + | \,\,\,\mathrm{as}\,\,x\to-\infty. | ||
| + | </math></center> | ||
| + | |||
| + | Note that <math>R_{\kappa}</math> and <math>T_{\kappa}</math> are the reflection and | ||
| + | transmission coefficients respectively and that we have normalized so | ||
| + | that the amplitude (in displacement) is unity. Also <math>k = - \mathrm{i} k_0</math>. | ||
| + | |||
| + | |||
| + | and we will consider both <math>k(\omega)</math> and <math>\omega(k)</math> | ||
| + | in what follows as required. The solution of the single-frequency | ||
| + | equation may be computationally challenging and for the generalized | ||
| + | eigenfunction expansion the major numerical work is to determine the | ||
| + | single-frequency solutions. | ||
As mentioned previously, determining <math>\zeta_\kappa</math> is the major | As mentioned previously, determining <math>\zeta_\kappa</math> is the major | ||
computation of the generalized eigenfunction method, but we simply | computation of the generalized eigenfunction method, but we simply | ||
| Line 301: | Line 175: | ||
R_1 T_{-1}^{*} + R_{-1}^{*} T_{1}=0, | R_1 T_{-1}^{*} + R_{-1}^{*} T_{1}=0, | ||
</math></center> | </math></center> | ||
| − | [[ | + | [[Mei 1983]]. |
It therefore follows that | It therefore follows that | ||
<center><math> | <center><math> | ||
| Line 309: | Line 183: | ||
_{2}\right) \delta_{\kappa\kappa^{\prime}}, | _{2}\right) \delta_{\kappa\kappa^{\prime}}, | ||
</math></center> | </math></center> | ||
| − | but we need to determine the normalizing function < | + | but we need to determine the normalizing function |
| − | + | <math>\Lambda_{n}\left( \omega_{n}\right)</math>. This is achieved by using the result that the | |
eigenfunctions satisfy the same normalizing condition with and without | eigenfunctions satisfy the same normalizing condition with and without | ||
the scatterers present. This result, the proof of which is quite | the scatterers present. This result, the proof of which is quite | ||
technical, is well-known and has been shown for many different | technical, is well-known and has been shown for many different | ||
situations. The original proof was for Schr\"odinger's equation and was | situations. The original proof was for Schr\"odinger's equation and was | ||
| − | due to [[ | + | due to [[Povzner 1953]] and [[Ikebe 1960]]. A proof for the case of Helmholtz |
| − | equation was given by [[ | + | equation was given by [[Wilcox 1975]]. Recently the proof was given |
| − | for water waves by [[ | + | for water waves by [[Hazard and Lenoir 2002]] and [[Hazard and Loret 2007]]. |
Since the eigenfunctions satisfy the same normalizing condition with | Since the eigenfunctions satisfy the same normalizing condition with | ||
| Line 331: | Line 205: | ||
& =2\pi \delta_{\kappa\kappa^{\prime}}\delta\left( k_{1}-k_{2}\right) \\ | & =2\pi \delta_{\kappa\kappa^{\prime}}\delta\left( k_{1}-k_{2}\right) \\ | ||
& =2\pi\delta_{\kappa\kappa^{\prime}}\delta\left( \omega_{1}-\omega_{2}\right) | & =2\pi\delta_{\kappa\kappa^{\prime}}\delta\left( \omega_{1}-\omega_{2}\right) | ||
| − | \left. \frac{d\omega}{ | + | \left. \frac{\mathrm{d}\omega}{\mathrm{d}k}\right\vert _{\omega=\omega_{1}}. |
\end{matrix}</math></center> | \end{matrix}</math></center> | ||
This result allows us to calculate the time-dependent solution in the | This result allows us to calculate the time-dependent solution in the | ||
| Line 347: | Line 221: | ||
g_{\kappa}\left( \omega\right) | g_{\kappa}\left( \omega\right) | ||
\frac{\sin(\omega t)}{\omega}\right\} | \frac{\sin(\omega t)}{\omega}\right\} | ||
| − | \zeta_{\kappa}(x,k) d\omega, | + | \zeta_{\kappa}(x,k) \mathrm{d}\omega, |
| − | |||
</math></center> | </math></center> | ||
where <math>f_\kappa</math> and <math>g_\kappa</math> will be determined from the initial | where <math>f_\kappa</math> and <math>g_\kappa</math> will be determined from the initial | ||
| Line 359: | Line 232: | ||
\zeta_0\left( x\right) | \zeta_0\left( x\right) | ||
,\zeta_{\kappa}(x,k)\right\rangle _{\mathcal{H}}=2\pi f_{\kappa}\left( | ,\zeta_{\kappa}(x,k)\right\rangle _{\mathcal{H}}=2\pi f_{\kappa}\left( | ||
| − | \omega\right) \frac{d\omega}{ | + | \omega\right) \frac{\mathrm{d}\omega}{\mathrm{d}k}, |
</math></center> | </math></center> | ||
and | and | ||
<center><math> | <center><math> | ||
\left\langle | \left\langle | ||
| − | + | \partial_t\zeta_0\left( x\right) | |
,\zeta_{\kappa}(x,k)\right\rangle _{\mathcal{H}}=2\pi g_{\kappa}\left( | ,\zeta_{\kappa}(x,k)\right\rangle _{\mathcal{H}}=2\pi g_{\kappa}\left( | ||
| − | \omega\right) \frac{d\omega}{ | + | \omega\right) \frac{\mathrm{d}\omega}{\mathrm{d}k}. |
</math></center> | </math></center> | ||
| − | We can therefore write | + | We can therefore write, changing the |
variable of integration to <math>k</math>, as | variable of integration to <math>k</math>, as | ||
| − | + | <center><math> | |
\zeta\left( x,t\right) | \zeta\left( x,t\right) | ||
=\frac{1}{2\pi}\int_{\mathbb{R}^{+}} \sum_{\kappa\in\left\{ -1,1\right\}} | =\frac{1}{2\pi}\int_{\mathbb{R}^{+}} \sum_{\kappa\in\left\{ -1,1\right\}} | ||
| Line 376: | Line 249: | ||
\left\langle \zeta_0\left( x\right) | \left\langle \zeta_0\left( x\right) | ||
,\zeta_{\kappa}(x,k)\right\rangle _{\mathcal{H}} | ,\zeta_{\kappa}(x,k)\right\rangle _{\mathcal{H}} | ||
| − | \cos(\omega t) | + | \cos(\omega t) |
+ \left\langle | + \left\langle | ||
| − | + | \partial_t \zeta_0\left( x\right) | |
,\zeta_{\kappa}(x,k)\right\rangle _{\mathcal{H}} | ,\zeta_{\kappa}(x,k)\right\rangle _{\mathcal{H}} | ||
\frac{\sin(\omega t)}{\omega}\Big\} | \frac{\sin(\omega t)}{\omega}\Big\} | ||
| − | \zeta_{\kappa}(x,k) | + | \zeta_{\kappa}(x,k) \mathrm{d}k, |
| − | + | </math></center> | |
| − | \ | ||
| − | If we take the case when <math> | + | If we take the case when <math>\partial_t\zeta_0( x) =0</math> and |
write the integral given by the inner product explicitly, we obtain | write the integral given by the inner product explicitly, we obtain | ||
<center><math> | <center><math> | ||
| Line 391: | Line 263: | ||
-1,1\right\} }\left( \frac{1}{2\pi}\int_{F}\zeta_0\left( x^{\prime}\right) | -1,1\right\} }\left( \frac{1}{2\pi}\int_{F}\zeta_0\left( x^{\prime}\right) | ||
\zeta_{\kappa}(x^{\prime},k) ^{*}\,\mathrm{d} x^{\prime}\right) | \zeta_{\kappa}(x^{\prime},k) ^{*}\,\mathrm{d} x^{\prime}\right) | ||
| − | \zeta_{\kappa}(x,k)\Big\}\cos(\omega t) | + | \zeta_{\kappa}(x,k)\Big\}\cos(\omega t)\mathrm{d}k. |
</math></center> | </math></center> | ||
| + | == Case of a [[Trapped Modes|trapped mode]] == | ||
| − | + | If the scattering structure supports a [[Trapped Modes|trapped mode]] at a particular | |
| − | + | frequency <math>\omega_{0}</math> then the expression for the free-surface elevation becomes | |
| − | + | <center><math> | |
| − | + | \zeta\left( x,t\right) =\int_{\mathbb{R}^{+}}\Big\{ \sum_{\kappa\in\left\{ | |
| − | + | -1,1\right\} }\left( \frac{1}{2\pi}\int_{F}\zeta_0\left( x^{\prime}\right) | |
| − | + | \zeta_{\kappa}(x^{\prime},k) ^{*}\,\mathrm{d} x^{\prime}\right) | |
| − | + | \zeta_{\kappa}(x,k)\Big\}\cos(\omega t)\mathrm{d}k + \left(\frac{\int_{F}\zeta_{0}(x^{\prime})\tilde\zeta(x^{\prime})^{*}\mathrm{d}x^{\prime} } | |
| − | + | {\int_{F}\tilde\zeta(x^{\prime})\tilde\zeta(x^{\prime})^{*}\mathrm{d}x^{\prime} }\right)\tilde\zeta(x)\cos(\omega_{0} t) | |
| − | + | </math></center> | |
| − | + | <center><math> | |
| − | + | + \int_{\mathbb{R}^{+}}\Big\{ \sum_{\kappa\in\left\{ | |
| − | + | -1,1\right\} }\left( \frac{1}{2\pi}\int_{F}\partial_t\zeta_0\left( x^{\prime}\right) | |
| − | + | \zeta_{\kappa}(x^{\prime},k) ^{*}\,\mathrm{d} x^{\prime}\right) | |
| + | \zeta_{\kappa}(x,k)\Big\}\frac{\sin(\omega t)}{\omega} \mathrm{d}k | ||
| + | + \left(\frac{\int_{F} | ||
| + | \partial_t\zeta_{0}(x^{\prime})\tilde\zeta(x^{\prime})^{*}\mathrm{d}x^{\prime} }{\int_{F} | ||
| + | \tilde\zeta(x^{\prime})\tilde\zeta(x^{\prime})^{*}\mathrm{d}x^{\prime} }\right)\tilde\zeta(x)\frac{\sin(\omega_{0} t)}{\omega_0} | ||
| + | </math></center> | ||
| + | where <math>\tilde\zeta(x)</math> is the trapped mode free-surface elevation. This | ||
| + | formula can be extend to the case when there is more than one trapped mode. | ||
==An identity linking waves from the left and right== | ==An identity linking waves from the left and right== | ||
| Line 421: | Line 301: | ||
must be purely real. This can only be true if | must be purely real. This can only be true if | ||
<center><math> | <center><math> | ||
| − | |||
\Im \left\{ \zeta_{1}(x^\prime,k)^{*} \zeta_{1}(x,k) \right\} | \Im \left\{ \zeta_{1}(x^\prime,k)^{*} \zeta_{1}(x,k) \right\} | ||
= | = | ||
| Line 427: | Line 306: | ||
\,\,\,x,x^{\prime} \in F. | \,\,\,x,x^{\prime} \in F. | ||
</math></center> | </math></center> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | == Matlab Code == | ||
| + | *A program to solve two small docks [http://www.math.auckland.ac.nz/~meylan/code/gem/gem_two_small_dock.m gem_two_small_dock.m] | ||
| + | with output shown on the right | ||
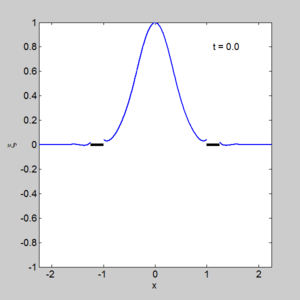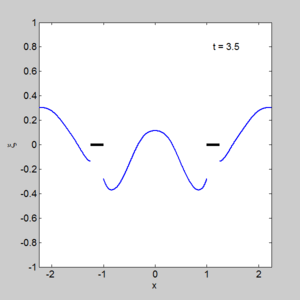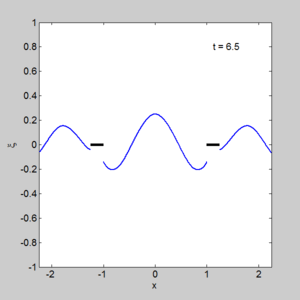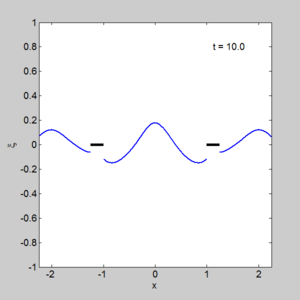
| + | [[Image:Small dock gem2.gif|300px|right|thumb|The evolution of an initial surface displacement, with two docks | ||
| + | as shown]] | ||
| + | === Additional code === | ||
| + | This program requires | ||
| − | + | * {{k_integrate}} | |
| − | + | * {{two docks eigenfunction matching symmetry}} | |
| − | + | * {{free surface dispersion equation code}} | |
| − | + | * {{gif_add_frame}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
[[Category:Time-Dependent Linear Water Waves]] | [[Category:Time-Dependent Linear Water Waves]] | ||
Latest revision as of 00:26, 25 February 2010
Introduction
The generalized eigenfunction method goes back to the work of Povzner 1953 and Ikebe 1960. The generalized eigenfunction method has been applied to water-wave problems by Friedman and Shinbrot 1967, Hazard and Lenoir 2002 (for the case of a rigid body in water of infinite depth) and Meylan 2002 (for a thin plate on water of shallow draft). We will present here the theory for a rigid body in water of finite depth. rms of this solutions (which we call the generalised eigenfunctions) because they solve for
The generalized eigenfunction method is based on an inner product in which the evolution operator is self-adjoint. It follows from the self-adjointness that we can expand the solution in the eigenfunctions of the operator. These eigenfunctions are nothing more than the single-frequency solutions. The main difficulty is that the eigenfunctions are associated with a continuous spectrum, and this requires that they be carefully normalized. Once this is done, we can derive simple expressions which allow the time-domain problem to be solved in terms of the single-frequency solutions. The mathematical ideas are discussed in detail in Hazard and Loret 2007.
We consider a two-dimensional fluid domain of constant depth, which
contains a finite number of fixed bodies of arbitrary geometry. We
denote the fluid domain by [math]\displaystyle{ \Omega }[/math], the boundary of the fluid domain
which touches the fixed bodies by [math]\displaystyle{ \partial\Omega }[/math], and the free
surface by [math]\displaystyle{ F. }[/math] The [math]\displaystyle{ x }[/math] and [math]\displaystyle{ z }[/math] coordinates are such that [math]\displaystyle{ x }[/math] is
pointing in the horizontal direction and [math]\displaystyle{ z }[/math] is pointing in the
vertical upwards direction (we denote [math]\displaystyle{ \mathbf{x}=\left( x,z\right) ). }[/math] The
free surface is at [math]\displaystyle{ z=0 }[/math] and the sea floor is at [math]\displaystyle{ z=-h }[/math]. The
fluid motion is described by a velocity potential [math]\displaystyle{ \Phi }[/math] and free surface by
[math]\displaystyle{ \zeta }[/math].
The equations of motion in the time domain are Laplace's equation through out the fluid
At the bottom surface we have no flow
At the free surface we have the kinematic condition
and the dynamic condition (the linearized Bernoulli equation)
The body boundary condition for a fixed body is
The initial conditions are
Equations in the Frequency Domain
We also assume that Frequency Domain Problem with frequency [math]\displaystyle{ \omega }[/math] and we assume that all variables are proportional to [math]\displaystyle{ \exp(-\mathrm{i}\omega t)\, }[/math]
The water motion is represented by a velocity potential which is denoted by [math]\displaystyle{ \phi\, }[/math] so that
[math]\displaystyle{ \Phi(\mathbf{x},t) = \mathrm{Re} \left\{\phi(\mathbf{x},\omega)e^{-\mathrm{i} \omega t}\right\}. }[/math]
The equations are the following
(note that the last expression can be obtained from combining the expressions:
where [math]\displaystyle{ \alpha = \omega^2/g \, }[/math]) The body boundary condition for a rigid body is just
The equation is subject to some radiation conditions at infinity. We assume the following.
[math]\displaystyle{ \phi^{\mathrm{I}}\, }[/math]
is a plane wave travelling in the [math]\displaystyle{ x }[/math] direction,
where [math]\displaystyle{ A }[/math] is the wave amplitude (in potential) [math]\displaystyle{ \mathrm{i} k }[/math] is the positive imaginary solution of the Dispersion Relation for a Free Surface (note we are assuming that the time dependence is of the form [math]\displaystyle{ \exp(-\mathrm{i}\omega t) }[/math]) and
In two-dimensions the Sommerfeld Radiation Condition is
where [math]\displaystyle{ \phi^{\mathrm{{I}}} }[/math] is the incident potential.
Time domain calculations
The solution in the frequency domain can be used to construct the solution in the time domain. This is well-known for the case of a plane incident wave which is initially far from the body, and in this case the solution can be calculated straightforwardly using the standard Fourier transform. However, when we consider an initial displacement which is non-zero around the bodies, we cannot express the time-dependent solution in terms of the single frequency solutions by a standard Fourier transform.
We begin with the equations in the time domain subject to the initial conditions given by Denoting the potential at the surface by
we introduce the operator [math]\displaystyle{ \mathbf{G} }[/math] which maps the surface potential to the potential throughout the fluid domain. The operator [math]\displaystyle{ \mathbf{G}\psi }[/math] is found by solving
and is defined by [math]\displaystyle{ \mathbf{G}\psi=\Psi. }[/math] The operator [math]\displaystyle{ \partial_{n}\mathbf{G} }[/math], which maps the surface potential to the normal derivative of potential at the surface (called the Dirichlet-to-Neumann map) is given by
Therefore the equations in the time domain can be written as
where we can recover the potential using the operator [math]\displaystyle{ \mathbf{G} }[/math]. The evolution operator [math]\displaystyle{ \partial_{n}\mathbf{G} }[/math] is symmetric in the Hilbert space given by the following inner product
where [math]\displaystyle{ * }[/math] denotes complex conjugate, and we assume that this symmetry implies that the operator is self-adjoint. We can prove the symmetry by using Green's second identity
where [math]\displaystyle{ \phi }[/math] and [math]\displaystyle{ \psi }[/math] are the surface potentials associated with [math]\displaystyle{ \zeta }[/math] and [math]\displaystyle{ \eta }[/math] respectively.
Eigenfunctions of [math]\displaystyle{ \partial_{n}\mathbf{G} }[/math]
The eigenfunctions of [math]\displaystyle{ \partial_{n}\mathbf{G} }[/math] satisfy
To solve for the eigenfunctions of [math]\displaystyle{ \partial_{n}\mathbf{G} }[/math] we need to solve the frequency-domain equations, and the radian frequency [math]\displaystyle{ \omega }[/math] is exactly the eigenvalue. To actually calculate the eigenfunctions of [math]\displaystyle{ \partial_{n}\mathbf{G} }[/math] we need to specify the incident wave potential, and for each frequency we have two eigenfunctions (waves incident from the left and from the right). It is possible for there to exist point spectra for this operator which correspond to the existence of a trapped mode McIver 1996 and the presence of a trapped mode requires that the generalized eigenfunction expansion we derive must be modified.
Normalization of the Eigenfunctions
The eigenfunctions of [math]\displaystyle{ \partial_{n}\mathbf{G} }[/math] (with eigenvalue [math]\displaystyle{ \omega }[/math]) are denoted by [math]\displaystyle{ \zeta_{\kappa}(x,k\left( \omega\right) ) }[/math], where [math]\displaystyle{ \kappa = \pm 1 }[/math] for waves incident from the left or right respectively. We must also specify radiations conditions to normalize the eigenfunctions and they are given by
Note that [math]\displaystyle{ R_{\kappa} }[/math] and [math]\displaystyle{ T_{\kappa} }[/math] are the reflection and transmission coefficients respectively and that we have normalized so that the amplitude (in displacement) is unity. Also [math]\displaystyle{ k = - \mathrm{i} k_0 }[/math].
and we will consider both [math]\displaystyle{ k(\omega) }[/math] and [math]\displaystyle{ \omega(k) }[/math]
in what follows as required. The solution of the single-frequency
equation may be computationally challenging and for the generalized
eigenfunction expansion the major numerical work is to determine the
single-frequency solutions.
As mentioned previously, determining [math]\displaystyle{ \zeta_\kappa }[/math] is the major
computation of the generalized eigenfunction method, but we simply
assume that they are known. We know that the eigenfunctions are
orthogonal for different [math]\displaystyle{ \omega }[/math] (from the self-adjointness of
[math]\displaystyle{ \partial_n\mathbf{G} }[/math]), and that the waves incident from the left and right
with the same [math]\displaystyle{ \omega }[/math] are orthogonal from the identity
Mei 1983. It therefore follows that
but we need to determine the normalizing function [math]\displaystyle{ \Lambda_{n}\left( \omega_{n}\right) }[/math]. This is achieved by using the result that the eigenfunctions satisfy the same normalizing condition with and without the scatterers present. This result, the proof of which is quite technical, is well-known and has been shown for many different situations. The original proof was for Schr\"odinger's equation and was due to Povzner 1953 and Ikebe 1960. A proof for the case of Helmholtz equation was given by Wilcox 1975. Recently the proof was given for water waves by Hazard and Lenoir 2002 and Hazard and Loret 2007.
Since the eigenfunctions satisfy the same normalizing condition with and without the scatterers, we normalize with the scatterers absent. This means that the eigenfunctions are simply the incident waves, and the free surface [math]\displaystyle{ F }[/math] is the entire axis. This allows us to derive
This result allows us to calculate the time-dependent solution in the eigenfunctions (or single-frequency solutions).
Expansion in Eigenfunctions
We expand the solution for the displacement in the time domain as
where [math]\displaystyle{ f_\kappa }[/math] and [math]\displaystyle{ g_\kappa }[/math] will be determined from the initial conditions. Note that here, and in subsequent equations, we are assuming that [math]\displaystyle{ k }[/math] is a function of [math]\displaystyle{ \omega }[/math] or that [math]\displaystyle{ \omega }[/math] is a function of [math]\displaystyle{ k }[/math] as required. If we take the inner product with respect to the eigenfunctions [math]\displaystyle{ \zeta_\kappa }[/math] we obtain
and
We can therefore write, changing the variable of integration to [math]\displaystyle{ k }[/math], as
If we take the case when [math]\displaystyle{ \partial_t\zeta_0( x) =0 }[/math] and write the integral given by the inner product explicitly, we obtain
Case of a trapped mode
If the scattering structure supports a trapped mode at a particular frequency [math]\displaystyle{ \omega_{0} }[/math] then the expression for the free-surface elevation becomes
where [math]\displaystyle{ \tilde\zeta(x) }[/math] is the trapped mode free-surface elevation. This formula can be extend to the case when there is more than one trapped mode.
An identity linking waves from the left and right
A consequence of the requirement that the displacement be real, if the initial displacement and initial derivative of displacement is real, is that
must be purely real. This can only be true if
Matlab Code
- A program to solve two small docks gem_two_small_dock.m
with output shown on the right
Additional code
This program requires
- Calculate Fourier integral k_integrate.m
- A program to calculate the coefficients for the finite dock problems can be found here two_finite_docks_symmetry.m
- dispersion_free_surface.m
- gif_add_frame.m