Linear Wave-Body Interaction

Wave and Wave Body Interactions
Current Chapter	Linear Wave-Body Interaction
Next Chapter	Added-Mass, Damping Coefficients And Exciting Forces
Previous Chapter	Ship Kelvin Wake

This is an incomplete page

Rigid body motions

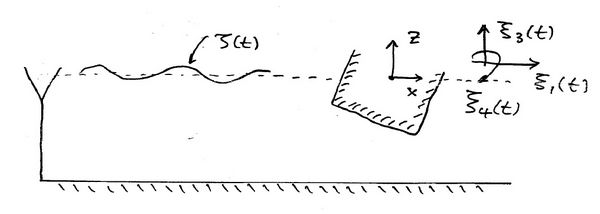
We consider a Linear Plane Progressive Regular Wave interacting with a floating body in two dimensions (the main concepts survive almost with no change in the more practical three-dimensional problem).

Introduction

We derive here the equations of motion for a body in Linear Plane Progressive Regular Waves in the frequency domain in two dimensions. We begin with the equations for a fixed body and then consider the equations for a rigid body.

Frequency Domain Equations

We assume small amplitude so that we can linearise all the equations (see Linear and Second-Order Wave Theory). We also assume that Frequency Domain Problem with frequency [math]\displaystyle{ \omega }[/math] and we assume that all variables are proportional to [math]\displaystyle{ \exp(-\mathrm{i}\omega t)\, }[/math] The water motion is represented by a velocity potential which is denoted by [math]\displaystyle{ \phi\, }[/math] so that

[math]\displaystyle{ \Phi(\mathbf{x},t) = \mathrm{Re} \left\{\phi(\mathbf{x},\omega)e^{-\mathrm{i} \omega t}\right\}. }[/math]

The coordinate system is the standard Cartesian coordinate system with the [math]\displaystyle{ z- }[/math]axis pointing vertically up. The water surface is at [math]\displaystyle{ z=0 }[/math] and the region of interest is [math]\displaystyle{ -h\lt z\lt 0 }[/math]. There is a body which occupies the region [math]\displaystyle{ \Omega }[/math] and we denote the wetted surface of the body by [math]\displaystyle{ \partial\Omega }[/math] We denote [math]\displaystyle{ \mathbf{r}=(x,y) }[/math] as the horizontal coordinate in two or three dimensions respectively and the Cartesian system we denote by [math]\displaystyle{ \mathbf{x} }[/math]. We assume that the bottom surface is of constant depth at [math]\displaystyle{ z=-h }[/math]. Variable Bottom Topography can also easily be included.

The equations are the following

[math]\displaystyle{ \begin{align} \Delta\phi &=0, &-h\lt z\lt 0,\,\,\mathbf{x} \in \Omega \\ \partial_z\phi &= 0, &z=-h, \\ \partial_z \phi &= \alpha \phi, &z=0,\,\,\mathbf{x} \in \partial \Omega_{\mathrm{F}}, \end{align} }[/math]

(note that the last expression can be obtained from combining the expressions:

[math]\displaystyle{ \begin{align} \partial_z \phi &= -\mathrm{i} \omega \zeta, &z=0,\,\,\mathbf{x} \in \partial \Omega_{\mathrm{F}}, \\ \mathrm{i} \omega \phi &= g\zeta, &z=0,\,\,\mathbf{x} \in \partial \Omega_{\mathrm{F}}, \end{align} }[/math]

where [math]\displaystyle{ \alpha = \omega^2/g \, }[/math])

[math]\displaystyle{ \partial_n\phi = \mathcal{L}\phi, \quad \mathbf{x}\in\partial\Omega_B, }[/math]

where [math]\displaystyle{ \mathcal{L} }[/math] is a linear operator which relates the normal and potential on the body surface through the physics of the body.

The simplest case is for a fixed body where the operator is [math]\displaystyle{ L=0 }[/math] and we will consider this boundary condition first before moving on to floating bodies.

The equation is subject to some radiation conditions at infinity. We assume the following. [math]\displaystyle{ \phi^{\mathrm{I}}\, }[/math] is a plane wave travelling in the [math]\displaystyle{ x }[/math] direction,

[math]\displaystyle{ \phi^{\mathrm{I}}(x,z)=A \phi_0(z) e^{\mathrm{i} k x} \, }[/math]

where [math]\displaystyle{ A }[/math] is the wave amplitude (in potential) [math]\displaystyle{ \mathrm{i} k }[/math] is the positive imaginary solution of the Dispersion Relation for a Free Surface (note we are assuming that the time dependence is of the form [math]\displaystyle{ \exp(-\mathrm{i}\omega t) }[/math]) and

[math]\displaystyle{ \phi_0(z) =\frac{\cosh k(z+h)}{\cosh k h} }[/math]

In two-dimensions the Sommerfeld Radiation Condition is

[math]\displaystyle{ \left( \frac{\partial}{\partial|x|} - \mathrm{i} k \right) (\phi-\phi^{\mathrm{{I}}})=0,\;\mathrm{{as\;}}|x|\rightarrow\infty\mathrm{.} }[/math]

where [math]\displaystyle{ \phi^{\mathrm{{I}}} }[/math] is the incident potential.

Equations for a Fixed Body in Frequency Domain

The equations for a fixed body are

[math]\displaystyle{ \begin{align} \Delta\phi &=0, &-h\lt z\lt 0,\,\,\mathbf{x} \in \Omega \\ \partial_z\phi &= 0, &z=-h, \\ \partial_z \phi &= \alpha \phi, &z=0,\,\,\mathbf{x} \in \partial \Omega_{\mathrm{F}}, \end{align} }[/math]

(note that the last expression can be obtained from combining the expressions:

[math]\displaystyle{ \begin{align} \partial_z \phi &= -\mathrm{i} \omega \zeta, &z=0,\,\,\mathbf{x} \in \partial \Omega_{\mathrm{F}}, \\ \mathrm{i} \omega \phi &= g\zeta, &z=0,\,\,\mathbf{x} \in \partial \Omega_{\mathrm{F}}, \end{align} }[/math]

where [math]\displaystyle{ \alpha = \omega^2/g \, }[/math]) The body boundary condition for a rigid body is just

[math]\displaystyle{ \partial_{n}\phi=0,\ \ \mathbf{x}\in\partial\Omega_{\mathrm{B}}, }[/math]

plus the radiation conditions.

We decompose the potential as

[math]\displaystyle{ \phi = \phi^{\mathrm{I}} + \phi^{\mathrm{D}} }[/math]

where [math]\displaystyle{ \phi^{\mathrm{I}} }[/math] is the incident potential and [math]\displaystyle{ \phi^{\mathrm{D}} }[/math] is the diffracted potential. The boundary condition for the diffracted potential is

[math]\displaystyle{ \Delta\phi^{\mathrm{D}}=0, \, -h\lt z\lt 0,\,\,\,\mathbf{x} \in \Omega }[/math] [math]\displaystyle{ \partial_n\phi^{\mathrm{D}} = 0, \, z=-h, }[/math] [math]\displaystyle{ \partial_n \phi^{\mathrm{D}} = \alpha \phi,\,z=0,\,\,\mathbf{x} \in F, }[/math]

plus

[math]\displaystyle{ \partial_n \phi^{\mathrm{D}} = - \partial_n \phi^{\mathrm{I}},\,\, \mathbf{x} \in \partial\Omega, }[/math]

Code to calculate the solution (using a slighly modified method) can be found Boundary Element Method for a Fixed Body in Finite Depth

Boundary Element Method for a Fixed Body in Finite Depth

Equations for a Floating Body in the Time Domain

The dynamic condition is the equation of motion for the structure in the frequency domain can be found from the time domain equations (Category:Time-Dependent Linear Water Waves) and are given by

[math]\displaystyle{ -\omega^2 M_{\mu\nu}\xi_{\nu}=-\mathrm{i}\omega\rho\iint_{\partial\Omega}\Phi n_{\mu}\, dS- C_{\mu\nu}\xi_{\nu},\quad \textrm{for} \qquad \mu=1,3,5, }[/math]

The equations of motion for [math]\displaystyle{ \zeta_\nu\, }[/math] follow from Newton's law applied to each mode in two dimensions. The same principles apply with very minor changes in three dimensions. We use the standard numbering of the modes of motion.

Equations for the Radiation Potential in Frequency Domain

We decompose the body motion into the rigid body modes of motion. Associated with each of these modes is a potential which must be solved for. The equations for the radiation potential in the frequency domain are

[math]\displaystyle{ \begin{align} \Delta\phi &=0, &-h\lt z\lt 0,\,\,\mathbf{x} \in \Omega \\ \partial_z\phi &= 0, &z=-h, \\ \partial_z \phi &= \alpha \phi, &z=0,\,\,\mathbf{x} \in \partial \Omega_{\mathrm{F}}, \end{align} }[/math]

(note that the last expression can be obtained from combining the expressions:

[math]\displaystyle{ \begin{align} \partial_z \phi &= -\mathrm{i} \omega \zeta, &z=0,\,\,\mathbf{x} \in \partial \Omega_{\mathrm{F}}, \\ \mathrm{i} \omega \phi &= g\zeta, &z=0,\,\,\mathbf{x} \in \partial \Omega_{\mathrm{F}}, \end{align} }[/math]

where [math]\displaystyle{ \alpha = \omega^2/g \, }[/math]) The body boundary condition for a radiation mode [math]\displaystyle{ m }[/math] is just

[math]\displaystyle{ \partial_{n}\phi=\mathbf{n}_\nu,\ \ \mathbf{x}\in\partial\Omega_{\mathrm{B}}, }[/math]

where [math]\displaystyle{ \mathbf{n}_{\nu} }[/math] is the normal derivative of the [math]\displaystyle{ \nu }[/math] mode on the body surface directed out of the fluid.

In two-dimensions the Sommerfeld Radiation Condition is

[math]\displaystyle{ \left( \frac{\partial}{\partial|x|}-k_0\right) \phi=0,\;\mathrm{{as\;}}|x|\rightarrow\infty\mathrm{.} }[/math]

Code to calculate the radiation potential can be found in Boundary Element Method for the Radiation Potential in Finite Depth

We denote the solution for each of the radiation potentials by [math]\displaystyle{ \phi_\nu^{\mathrm{R}} }[/math] and the total potential is written as

[math]\displaystyle{ \phi = \phi^{\mathrm{I}} + \phi^{\mathrm{D}} + \sum_\nu \zeta_\nu \phi_\nu^{\mathrm{R}} }[/math]

Added Mass and Damping.

We substitute the expansion for the potential into the equations in the frequency domain and we obtain

[math]\displaystyle{ -\omega^2 M_{\mu\nu}\xi_{\nu}=-\mathrm{i}\omega\rho\iint_{\partial\Omega_{B}} \left(\phi^{\mathrm{I}} + \phi^{\mathrm{D}} + \sum_{\lambda} \zeta_\lambda \phi_{\lambda}^{\mathrm{R}}\right) n_{\mu}\, dS- C_{\mu\nu}\xi_{\nu},\quad \textrm{for} \qquad \mu=1,3,5, }[/math]

We then define the matrices

[math]\displaystyle{ A_{\lambda\mu} = \mathrm{Re} \left\{ -\frac{\mathrm{i}}{\omega}\rho\iint_{\partial\Omega_{B}} \phi_m^{\mathrm{R}} n_{\mu}\, dS \right\} }[/math]

which is called the added mass matrix and We then define the matrices

[math]\displaystyle{ B_{\lambda\mu} = \mathrm{Im} \left\{ -\rho\iint_{\partial\Omega_{B}} \phi_m^{\mathrm{R}} n_{\mu}\, dS \right\} }[/math]

which is called the mass matrix then the equations can be expressed as follows.

Surge

[math]\displaystyle{ \sum_j \left[ -\omega^2 \left( M_{1j} + A_{1j} \right) + i\omega B_{1j} + C_{1j} \right] \zeta_j = F_1 (\omega), \quad j=1,3,5 }[/math]

Heave

[math]\displaystyle{ \sum_j \left[ -\omega^2 \left( M_{3j} + A_{3j} \right) + i\omega B_{3j} + C_{3j} \right] \zeta_j = F_3 (\omega), \quad j=1,3,5 }[/math]

Pitch

[math]\displaystyle{ \sum_j \left[ -\omega^2 \left( M_{5j} + A_{5j} \right) + i\omega B_{5j} + C_{5j} \right] \zeta_j = F_5 (\omega) , \quad j=1,3,5 }[/math]

The extension of these equations to six degrees of freedom is straightforward. However before discussing the general case we will study specific properties of the 2D Problem for the sake of clarity.

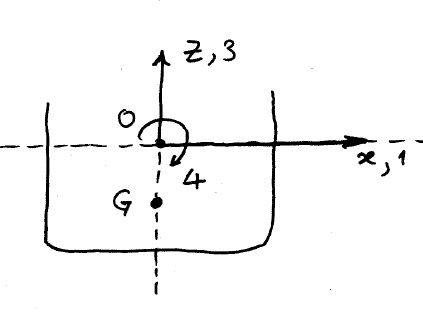
Symmetric body

Consider a body symmetric about the [math]\displaystyle{ X = 0\, }[/math] axis.

Symmetric body

For a body symmetric port/starboard:

• Verify that Heave is decoupled from Surge and Roll. In other words the Surge and Roll motions do not influence Heave and vice versa:

[math]\displaystyle{ \left[ -\omega^2 \left( M + A_{33} \right) + i\omega B_{33} + C_{33} \right] \Pi_3 = A }[/math]

• The only nonzero hydrostatic coefficients are [math]\displaystyle{ C_{33} \, }[/math] and [math]\displaystyle{ C_{44} \, }[/math]. Verify that this is the case even for non-symmetric sections.

• Surge and Roll are coupled for symmetric and non-symmetric bodies. The coupled equation of motion becomes:

Surge-Roll

[math]\displaystyle{ \sum_{j=1,4} \left[ -\omega^2 \left( M_{ij} + A_{ij} \right) + i\omega B_{ij} + C_{ij} \right] \Pi_j = \mathbf{X}_i, \quad i,j = 1,4 }[/math]

• When Newton's law is expressed about the center of gravity:

[math]\displaystyle{ M_{14} = M_{41} = 0, \ M_{11} = M, \ M_{44} = I_G }[/math]

where [math]\displaystyle{ I_G\, }[/math] is the body moment of inertia about the center of gravity. If the equations are to be expressed about the origin of the coordinate system, then the formulation must start with respect to [math]\displaystyle{ G\, }[/math] and expressions derived w.r.t. [math]\displaystyle{ O \, }[/math], via a coordinate transformation.

• The exciting forces [math]\displaystyle{ \mathbf{X}_1, \mathbf{X}_3 \, }[/math] are defined in an obvious manner along the X- and Z-axis. The Roll moment [math]\displaystyle{ \mathbf{X}_4 \, }[/math] is defined initially about [math]\displaystyle{ G\, }[/math].

Need to derive definitions for the coefficients that enter the Heave & Surge-Roll equations of motion:

[math]\displaystyle{ M = \rho \forall, \qquad \forall = \ }[/math] volume of water displaced by body (archimedian principle of buoyancy) [math]\displaystyle{ C_{33} = \rho g A_\omega = \rho g B, }[/math] [math]\displaystyle{ A_\omega = }[/math] body waterplane area = [math]\displaystyle{ B }[/math] (Beam in two dimensions) [math]\displaystyle{ \left( C_{44} \right)_G = \rho g \frac{B^3}{12} = \ }[/math] Roll restoring moment due to a small angular displacement about the center of gravity. Verify for all wall and non-wall sided sections [math]\displaystyle{ C_{44} \equiv \left( C_{44} \right)+G \ne \left( C_{44} \right)_O; \quad }[/math] Derive an expression for [math]\displaystyle{ \ \left( C_{44} \right)_O \ }[/math] in terms of [math]\displaystyle{ \ \left( C_{44} \right)_G. }[/math]

---

This article is based on the MIT open course notes and the original article can be found here