Difference between revisions of "Variable Depth Shallow Water Wave Equation"
Sean Curry (talk | contribs) |
|||
| (30 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | We consider here the problem of waves reflected by a region of variable depth in a finite region or in | |
| − | + | an otherwise uniform depth region assuming the equations of [[:Category:Shallow Depth|Shallow Depth]] (assuming the problem is linear). | |
| − | We consider here the problem of waves reflected by a region of variable depth in | + | We consider slightly more general equations of motion so that the same method could be used for a variable |
| − | an otherwise uniform depth region assuming the equations of [[:Category:Shallow Depth|Shallow Depth]]. | + | density string. |
== Equations == | == Equations == | ||
| Line 10: | Line 10: | ||
== Waves in a finite basin == | == Waves in a finite basin == | ||
| + | |||
| + | [[Image:finite_string.gif|right|A finite shallow basin with variable depth]] | ||
We consider the problem of waves in a finite basin <math>-L<x<L</math>. At the edge of the basin the boundary conditions are | We consider the problem of waves in a finite basin <math>-L<x<L</math>. At the edge of the basin the boundary conditions are | ||
| Line 89: | Line 91: | ||
</math></center> | </math></center> | ||
| − | === Matlab | + | === Matlab Code === |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Code to calculate the solution in a finite basin can be found here {{one dimensional shallow wave finite}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Waves in an infinite basin == | == Waves in an infinite basin == | ||
| Line 177: | Line 99: | ||
We assume that the density <math>\rho</math> and the depth <math>h</math> are constant and equal to one outside the region <math>-L<x<L</math>. | We assume that the density <math>\rho</math> and the depth <math>h</math> are constant and equal to one outside the region <math>-L<x<L</math>. | ||
We can therefore write the wave as | We can therefore write the wave as | ||
| + | <center><math>u(x,t) = e^{-i k x} + R e^{i k x},\,\,x<-L</math></center> | ||
| + | <center><math>u(x,t) = Te^{-i k x},\,\,x<-L</math></center> | ||
| + | for waves incident from the right. To solve we use a solution to the problem on the interval | ||
| + | <math>-L<x<L</math> subject to arbitrary boundary conditions and match. | ||
| − | == Solution | + | === Solution in Finite Interval of Variable Properties === |
Taking a separable solution gives the eigenvalue problem | Taking a separable solution gives the eigenvalue problem | ||
<center> | <center> | ||
| − | <math>\partial_x \left( h(x) \partial_x\zeta \right) = -\ | + | <math>\partial_x \left( h(x) \partial_x\zeta \right) = -\omega^{2}\rho(x)\zeta \quad (1)</math> |
</center> | </center> | ||
| Line 189: | Line 115: | ||
Substituting this form into (1) gives | Substituting this form into (1) gives | ||
<center> | <center> | ||
| − | <math> \partial_x(h(x)\partial_x \zeta_p)+\partial_x(h(x)\partial_xu) = -\ | + | <math> \partial_x(h(x)\partial_x \zeta_p)+\partial_x(h(x)\partial_xu) = -\omega^{2}\left(\zeta_p+u\right)</math> |
</center> | </center> | ||
Or, on rearranging | Or, on rearranging | ||
<center> | <center> | ||
| − | <math> \partial_x(h(x)\partial_xu)+\ | + | <math> \partial_x(h(x)\partial_xu)+\omega^{2}u = -\partial_x(h(x)\partial_x \zeta_p)-\omega^{2}\zeta_p = f(x)\quad (2)</math> |
</center> | </center> | ||
| − | so <center><math> f(x) = -\frac{(b-a)}{2L}\partial_xh(x) - \ | + | so <center><math> f(x) = -\partial_x(h(x)\partial_x \zeta_p)-\omega^{2}\zeta_p = -\frac{(b-a)}{2L}\partial_xh(x) - \omega^2 \left(\frac{(b-a)}{2L}x + \frac{b+a}{2}\right) </math> |
</center> | </center> | ||
Now consider the homogenous Sturm-Liouville problem for u | Now consider the homogenous Sturm-Liouville problem for u | ||
| Line 214: | Line 140: | ||
Substituting the fourier expansion for <math>u_k</math> into (4): | Substituting the fourier expansion for <math>u_k</math> into (4): | ||
<center> | <center> | ||
| − | <math> J = \int_{-L}^{L}\,h\left(\sum_{n=1}^{\infty} a_{n} \psi_n'\right)^{2}-\lambda \rho \left(\sum_{n=1}^{\infty} a_{n} \psi_n\right)^{2} \, dx \quad | + | <math> J = \int_{-L}^{L}\,h\left(\sum_{n=1}^{\infty} a_{n} \psi_n'\right)^{2}-\lambda \rho \left(\sum_{n=1}^{\infty} a_{n} \psi_n\right)^{2} \, dx \quad </math></center> |
Since <math>u_k</math> minimises J, we require <math> \frac{\partial J}{\partial a_{n}}=0 \quad \forall n </math> | Since <math>u_k</math> minimises J, we require <math> \frac{\partial J}{\partial a_{n}}=0 \quad \forall n </math> | ||
<center> | <center> | ||
| Line 225: | Line 151: | ||
| − | By defining a vector <math> \textbf{a} = \left(a_{n}\right)</math> and matrices <math>K_{(n,m)} = \int_{-L}^{L}h(x)\psi_m'(x)\psi_n'(x)dx </math> and <math>M_{(n,m)} = \int_{-L}^{L}\rho(x)\psi_m(x)\psi_n(x)dx </math> we have the linear system <math> K\textbf{a} = \ | + | By defining a vector <math> \textbf{a} = \left(a_{n}\right)</math> and matrices <math>K_{(n,m)} = \int_{-L}^{L}h(x)\psi_m'(x)\psi_n'(x)dx </math> and <math>M_{(n,m)} = \int_{-L}^{L}\rho(x)\psi_m(x)\psi_n(x)dx </math> we have the linear system <math> K\textbf{a} = \lambda M\textbf{a} </math> which returns the eigenvalues and eigenvectors of equation (3), with eigenvectors <math> \textbf{a} </math> representing coefficient vectors of the fourier expansions of eigenfunctions. |
| + | If we now construct <math> u(x,\omega) = \sum_{k=1}^{\infty} b_k u_k </math> and substitute this into equation (2) we get | ||
| + | <center><math> \sum_{k=1}^{\infty} (\partial_x(h(x)\partial_x u_k) + \omega^{2}\rho u_k)b_k = f(x) </math></center> | ||
| + | <center><math> \implies \sum_{k=1}^{\infty} (-\lambda_k\rho u_k + \omega^{2}\rho u_k)b_k = f(x) </math></center> | ||
| + | <center><math> \implies \sum_{k=1}^{\infty} (\omega^{2}-\lambda_k) b_k \rho u_k = f(x) \quad (5) </math></center> | ||
| + | And defining the RHS of equation (5) as <math> f(x) </math>, a known function, we can retrieve the coefficients <math> b_k </math> by integrating against <math> u_k </math> | ||
| + | <center> | ||
| + | <math> b_k = \frac{\int_{-L}^{L}\,f u_k\,dx}{(\omega^{2}-\lambda_k) \int_{-L}^{L}\, \rho u_{k}^{2}\,dx} </math> | ||
| + | </center> | ||
| + | The coefficients <math> c_n </math> of the fourier expansion of u are just <math> \sum_{k=1}^{\infty}a_{n,k}b_{k} </math> with <math> a_{n.k} </math> being the <math>n</math>th coefficient of the <math>k</math>th eigenfunction of the Sturm-Liouville problem. | ||
| + | So | ||
| + | <center><math> \zeta(x,\omega)=\frac{(b-a)}{2L}x + \frac{b+a}{2}+\sum_{n=1}^{\infty}c_{n} \sin\left(\frac{n\pi}{2}\left(\frac{x}{L} + 1\right)\right), \quad (6)</math> </center> | ||
| + | with <math> \zeta |_{-L}=a \quad \zeta |_{L}=b </math> and, given <math> a </math> and <math> b </math> explicitly differentiating <math> \zeta </math> gives <math> \partial_x \zeta |_{-L} </math> and <math> \partial_x \zeta |_L </math>. | ||
| + | === Matching at <math>\pm L</math> === | ||
| + | We choose a basis of the solution space for any particular <math>\omega</math> to be <math>\{\zeta_1,\,\zeta_2\}</math>, where <math> \zeta_1 </math> is the solution to the BVP(a=1,b=0) and <math> \zeta_1 </math> is the solution to the BVP(a=0,b=1). The functions <math> \zeta_1 </math> and <math> \zeta_2 </math> can be calculated for any <math> \omega </math> from (6). | ||
| − | + | The aim here is to construct a matrix '''S''' such that, given <math> a </math> and <math> b </math> | |
<center> | <center> | ||
| − | <math> \ | + | <math> S \begin{pmatrix} \zeta |_{-L} \\ \zeta |_L \end{pmatrix}=\begin{pmatrix} \partial_x \zeta |_{-L} \\ \partial_x \zeta |_L \end{pmatrix}</math> |
</center> | </center> | ||
| − | + | ||
| + | Taking <math> a=1,\,b=0 </math> to give <math> \zeta_1 </math> shows that the first column of '''S''' must be <math> \begin{pmatrix} \partial_x \zeta_1 |_{-L} \\ \partial_x \zeta_1 |_L \end{pmatrix} </math> and likewise taking <math> a=0,\,b=1 </math> to give <math> \zeta_2 </math> shows the second column must be <math> \begin{pmatrix} \partial_x \zeta_2 |_{-L} \\ \partial_x \zeta_2 |_L \end{pmatrix} </math>. So '''S''' is given by | ||
<center> | <center> | ||
| − | <math> | + | <math> \begin{pmatrix} \partial_x \zeta_1 |_{-L} \, \partial_x \zeta_2 |_{-L} \\ \partial_x \zeta_1 |_L \, \partial_x \zeta_2 |_L \end{pmatrix} </math> |
</center> | </center> | ||
| − | + | Now for the area of constant depth on the left hand side there is a potential of the form <math> e^{i\omega x} </math> which, creates reflected and transmitted potentials from the variable depth area of the form <math> Re^{-i\omega x} </math> and <math> Te^{i\omega x} </math> respectively where the magnitudes of <math> R </math> and <math> T </math> are unknown. We can calculate that the boundary conditions for <math> \zeta </math> must be | |
| − | |||
| − | |||
| − | |||
| − | |||
<center> | <center> | ||
| − | <math> | + | <math> \zeta |_{-L} = e^{-i\omega L}+Re^{i\omega L}, \quad \zeta |_L = Te^{i\omega L}, \quad \partial_x \zeta |_{-L} = i\omega e^{-i\omega L}-i\omega Re^{i\omega L}, \quad \partial_x \zeta |_L = i\omega Te^{i\omega L} </math> |
</center> | </center> | ||
| − | |||
<center> | <center> | ||
| − | <math> \begin{pmatrix} \ | + | <math> \begin{pmatrix} i\omega e^{-i\omega L}-i\omega Re^{i\omega L} \\ i\omega Te^{i\omega L} \end{pmatrix} = S\begin{pmatrix} e^{-i\omega L}+Re^{i\omega L} \\ Te^{i\omega L} \end{pmatrix} </math> |
</center> | </center> | ||
| − | + | Knowing '''S''' these boundary conditions can be solved for <math> R</math> and <math>T</math>, which in turn gives actual numerical boundary conditions to the original problem(<math>a_+=e^{-i\omega L}+Re^{i\omega L}</math> and <math> b_+=Te^{i\omega L}</math>). Taking a linear combination of the solutions already calculated (<math> a_+\zeta_1(x,\omega) + b_+\zeta_2(x,\omega) </math>) will provide the solution for these new boundary conditions. This solution, along with the potentials outside this region gives a generalised eigenfunction potential for the whole real axis which we denote as <math> \zeta_+(x,\omega)</math>. | |
| − | <center> | + | |
| − | <math> \zeta | + | Independent generalised eigenfunctons (which we denote as <math> \zeta_-(x,\omega)</math>)can be found by considering the potential <math> e^{-i\omega x} </math> on the right hand region of constant depth. The corresponding reflected and transmitted potentials from the variable depth area are of the form <math> Re^{i\omega x} </math> and <math> Te^{-i\omega x} </math> respectively. Again knowing '''S''' we can solve for R and T and hence find the numerical boundary conditions (<math>a_-=Te^{i\omega L}</math> and <math>b_-=e^{-i\omega L}+Re^{i\omega L}</math>). |
| − | </center> | + | |
| + | We come out with: | ||
| + | |||
| + | <center><math> | ||
| + | \zeta_+(x,\omega) = \left\{ \begin{matrix} | ||
| + | {e^{i\omega x}+Re^{-i\omega x}, \quad \mbox{ for } x<-L} | ||
| + | \\ {a_+\zeta_1(x,\omega) + b_+\zeta_2(x,\omega),\quad \mbox{ for } -L\leq x \leq L} | ||
| + | \\ {Te^{i\omega x}, \quad \mbox{ for } x>L} | ||
| + | \end{matrix} \right. | ||
| + | </math></center> | ||
| + | |||
| + | where R and T are found by solving: | ||
| + | |||
| + | <center><math> | ||
| + | \begin{pmatrix} (S_{11} + i\omega)e^{i\omega L} & S_{12}e^{i\omega L} \\ | ||
| + | S_{21}e^{i\omega L} & (S_{22}-i\omega)e^{i\omega L} \end{pmatrix} \begin{pmatrix}R\\T\end{pmatrix} | ||
| + | = \begin{pmatrix} (i\omega - S_{11}) e^{-i\omega L} \\ -S_{21}e^{-i\omega L} \end{pmatrix} | ||
| + | </math></center> | ||
| + | |||
| + | and <math>a_+=e^{-i\omega L}+Re^{i\omega L}</math> and <math> b_+=Te^{i\omega L}</math> | ||
| + | |||
| + | |||
| + | Note that the values of R and T for <math>\zeta_-</math> are different from those for <math>\zeta_+</math> | ||
| + | (although they are related through some identities). For <math>\zeta_-</math> we have: | ||
| + | |||
| + | <center><math> | ||
| + | \zeta_-(x,\omega) = \left\{ \begin{matrix} | ||
| + | {Te^{-i\omega x}, \quad \mbox{ for } x<-L} | ||
| + | \\ {a_-\zeta_1(x,\omega) + b_-\zeta_2(x,\omega),\quad \mbox{ for } -L\leq x \leq L} | ||
| + | \\ {e^{-i\omega x}+Re^{i\omega x}, \quad \mbox{ for } x>L} | ||
| + | \end{matrix} \right. | ||
| + | </math></center> | ||
| + | |||
| + | where R and T are found by solving: | ||
| + | |||
| + | <center><math> | ||
| + | \begin{pmatrix} S_{12}e^{i\omega L} & (S_{11}+i\omega)e^{i\omega L} \\ | ||
| + | (S_{22}-i\omega)e^{i\omega L} & S_{21}e^{i\omega L}\end{pmatrix} \begin{pmatrix}R\\T\end{pmatrix} | ||
| + | = \begin{pmatrix} S_{12}e^{-i\omega L} \\ -(i\omega + S_{21})e^{-i\omega L} \end{pmatrix} | ||
| + | </math></center> | ||
| + | |||
| + | Note a_+, b_+, a_- and b_- are found frm their corresponding R and T values. | ||
| + | |||
| + | === Generalised Eigenfunction Expansion === | ||
| + | |||
| + | |||
| + | Now we have the generalised eigenfunctions <math>\zeta_+(x,\omega)</math> and <math>\zeta_-(x,\omega)</math>, which have the orthogonality relationships: | ||
| + | <center><math> | ||
| + | \int_{-\infty}^{\infty}\zeta_+(x,\omega)\zeta_-(x,\omega')\mathrm{d}x= 0 \qquad (7) | ||
| + | </math></center> | ||
| + | <center><math> | ||
| + | \int_{-\infty}^{\infty}\zeta_+(x,\omega)\zeta_+(x,\omega')\mathrm{d}x= 2 \pi \delta(\omega-\omega') \qquad (8) | ||
| + | </math></center> | ||
| + | <center><math> | ||
| + | \int_{-\infty}^{\infty}\zeta_-(x,\omega)\zeta_-(x,\omega')\mathrm{d}x= 2 \pi \delta(\omega-\omega') \qquad (9) | ||
| + | </math></center> | ||
| + | |||
| + | For any particular <math>\omega </math> the general solution to the differential equation can be written as: | ||
| + | <center><math> | ||
| + | \zeta(x,t,\omega) = \cos(\omega t)\left(c_1(\omega)\zeta_+(x,\omega)+d_1(\omega)\zeta_-(x,\omega)\right) + \frac{\sin(\omega t)}{\omega}\left(c_2(\omega)\zeta_+(x,\omega)+d_2(\omega)\zeta_-(x,\omega)\right) | ||
| + | </math></center> | ||
| + | The general solution to the PDE is therefore: | ||
| + | <center><math> | ||
| + | \zeta(x,t) = \int_{0}^{\infty} \zeta(x,t,\omega) \mathrm{d} \omega | ||
| + | </math></center> | ||
| + | <center><math> | ||
| + | \implies \zeta(x,t) = \int_{0}^{\infty} \left\{ \cos(\omega t)\left(c_1(\omega)\zeta_+(x,\omega)+d_1(\omega)\zeta_-(x,\omega)\right) | ||
| + | + \frac{\sin(\omega t)}{\omega}\left(c_2(\omega)\zeta_+(x,\omega)+d_2(\omega)\zeta_-(x,\omega)\right) | ||
| + | \right\} \mathrm{d} \omega \qquad (10) | ||
| + | </math></center> | ||
| + | |||
| + | |||
| + | Giving the initial conditions: | ||
| + | <center><math> | ||
| + | F(x) = \zeta(x,0) = \int_{0}^{\infty} \left\{ c_1(\omega)\zeta_+(x,\omega)+d_1(\omega)\zeta_-(x,\omega) \right\} \mathrm{d} \omega | ||
| + | </math></center> | ||
| + | <center><math> | ||
| + | G(x) = \partial_t \zeta(x,0) = \int_{0}^{\infty} \left\{ c_2(\omega)\zeta_+(x,\omega)+d_2(\omega)\zeta_-(x,\omega) \right\} \mathrm{d} \omega | ||
| + | </math></center> | ||
| − | + | Using identities (7),(8) and (9) we can show: | |
| + | <center><math> | ||
| + | c_1(\omega) = \frac{1}{2\pi}\langle F(x), \zeta_+(x,\omega) \rangle | ||
| + | </math></center> | ||
| + | <center><math> | ||
| + | d_1(\omega) = \frac{1}{2\pi}\langle F(x), \zeta_-(x,\omega) \rangle | ||
| + | </math></center> | ||
| + | <center><math> | ||
| + | c_2(\omega) = \frac{1}{2\pi}\langle G(x), \zeta_+(x,\omega) \rangle | ||
| + | </math></center> | ||
| + | <center><math> | ||
| + | d_2(\omega) = \frac{1}{2\pi}\langle G(x), \zeta_-(x,\omega) \rangle | ||
| + | </math></center> | ||
| − | + | Which we can use in combination with (10) to solve the IVP. | |
| − | |||
| − | |||
| − | |||
| − | + | === Matlab Code === | |
| − | |||
| − | |||
| − | |||
| − | + | Code to calculate the solution in a infinite basin can be found here {{one dimensional shallow wave infinite}} | |
[[Category:Shallow Depth]] | [[Category:Shallow Depth]] | ||
| + | [[Category:Simple Linear Waves]] | ||
| + | [[Category:Complete Pages]] | ||
Latest revision as of 03:04, 18 July 2009
We consider here the problem of waves reflected by a region of variable depth in a finite region or in an otherwise uniform depth region assuming the equations of Shallow Depth (assuming the problem is linear). We consider slightly more general equations of motion so that the same method could be used for a variable density string.
Equations
We begin with the shallow depth equation
subject to the initial conditions
where [math]\displaystyle{ \zeta }[/math] is the displacement, [math]\displaystyle{ \rho }[/math] is the string density and [math]\displaystyle{ h(x) }[/math] is the variable depth (note that we are unifying the variable density string and the wave equation in variable depth because the mathematical treatment is identical).
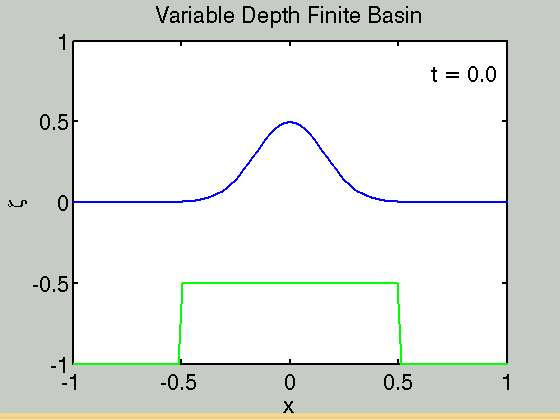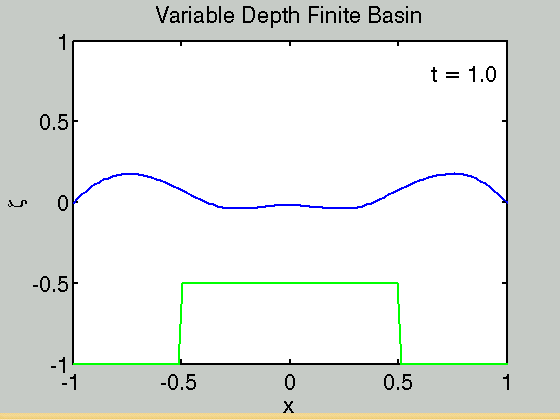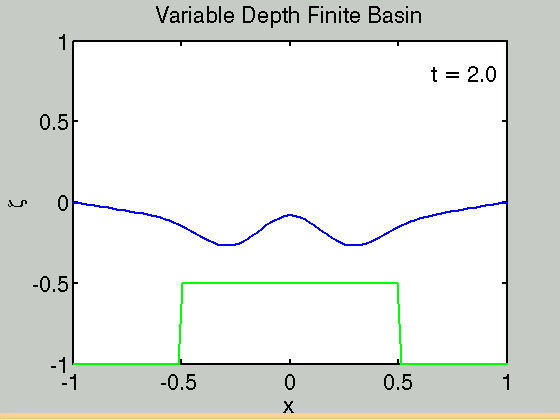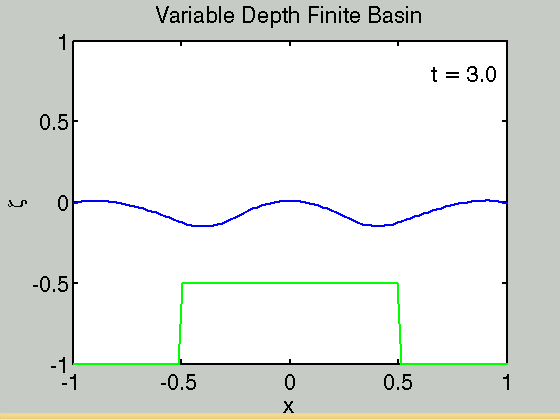
Waves in a finite basin
We consider the problem of waves in a finite basin [math]\displaystyle{ -L\lt x\lt L }[/math]. At the edge of the basin the boundary conditions are
.
We solve the equations by expanding in the modes for the basin which satisfy
normalised so that
The solution is then given by
where we have assumed that [math]\displaystyle{ \lambda_0 = 0 }[/math].
Calculation of [math]\displaystyle{ \zeta_n }[/math]
We can calculate the eigenfunctions [math]\displaystyle{ \zeta_n }[/math] by an expansion in the modes for the case of uniform depth. We use the Rayleigh-Ritz method. The eigenfunctions are local minimums of
[math]\displaystyle{ J[\zeta] = \int_{-L}^L \frac{1}{2}\left\{ h(x)\left(\partial_x \zeta\right)^2 - \lambda \rho(x) \zeta^2 \right\} }[/math]
subject to the boundary conditions that the normal derivative vanishes (where [math]\displaystyle{ \lambda }[/math] is the eigenvalue).
We expand the displacement in the eigenfunctions for constant depth [math]\displaystyle{ h=1 }[/math]
[math]\displaystyle{ \zeta = \sum_{n=0}^{N} a_n \psi_n(x) }[/math]
where
[math]\displaystyle{ \psi_n = \frac{1}{\sqrt{L}} \cos( n \pi (\frac{1}{2L}x + \frac{1}{2})),\,\,n\ne 1 }[/math]
[math]\displaystyle{ \psi_0 = \frac{1}{\sqrt{2L}},\, }[/math]
and substitute this expansion into the variational equation we obtain
this equation can be rewritten using matrices as
[math]\displaystyle{ \mathbf{K} \vec{a} = \lambda\mathbf{M} \vec{a} }[/math]
where the elements of the matrices K and M are
[math]\displaystyle{ \mathbf{K}_{mn} = \int_{-L}^L \left\{ \left(\partial_x \psi_m h(x) \partial_x \psi_n\right) \right\} }[/math]
and
Matlab Code
Code to calculate the solution in a finite basin can be found here finite_basin_variable_h_and_rho.m
Waves in an infinite basin
We assume that the density [math]\displaystyle{ \rho }[/math] and the depth [math]\displaystyle{ h }[/math] are constant and equal to one outside the region [math]\displaystyle{ -L\lt x\lt L }[/math]. We can therefore write the wave as
for waves incident from the right. To solve we use a solution to the problem on the interval [math]\displaystyle{ -L\lt x\lt L }[/math] subject to arbitrary boundary conditions and match.
Solution in Finite Interval of Variable Properties
Taking a separable solution gives the eigenvalue problem
[math]\displaystyle{ \partial_x \left( h(x) \partial_x\zeta \right) = -\omega^{2}\rho(x)\zeta \quad (1) }[/math]
Given boundary conditions [math]\displaystyle{ \zeta \mid_{-L} = a }[/math] and [math]\displaystyle{ \zeta \mid_L = b }[/math] we can take [math]\displaystyle{ \zeta = \zeta_p + u }[/math] With [math]\displaystyle{ \zeta_p = \frac{(b-a)}{2L}x + \frac{b+a}{2} }[/math] satisfying the boundary conditions and [math]\displaystyle{ u }[/math] satisfying [math]\displaystyle{ u |_{-L} = u |_L = 0 }[/math]
Substituting this form into (1) gives
[math]\displaystyle{ \partial_x(h(x)\partial_x \zeta_p)+\partial_x(h(x)\partial_xu) = -\omega^{2}\left(\zeta_p+u\right) }[/math]
Or, on rearranging
[math]\displaystyle{ \partial_x(h(x)\partial_xu)+\omega^{2}u = -\partial_x(h(x)\partial_x \zeta_p)-\omega^{2}\zeta_p = f(x)\quad (2) }[/math]
so
Now consider the homogenous Sturm-Liouville problem for u
[math]\displaystyle{ \partial_x(h(x)\partial_xu)+\lambda u = 0\quad u|_0=u|_1=0 \quad (3) }[/math]
By Sturm-Liouville theory this has an infinite set of eigenvalues [math]\displaystyle{ \lambda_k }[/math] with corresponding eigenfunctions [math]\displaystyle{ u_k }[/math]. Also since [math]\displaystyle{ u_k|_0=u_k|_1=0\quad \forall k }[/math] Each [math]\displaystyle{ u_k }[/math] can be expanded as a fourier series in terms of sine functions.
[math]\displaystyle{ u_k = \sum_{n=1}^{\infty} a_{n,k} \psi_n }[/math]
where
[math]\displaystyle{ \psi_n = \sin\left(\frac{n\pi}{2}\left(\frac{x}{L} + 1\right)\right) }[/math]
Transforming (3) into the equivalent variational problem gives
[math]\displaystyle{ J[u] = \int_{-L}^{L}\,hu'^{2}-\lambda \rho u^{2} \, dx \quad (4) }[/math]
Substituting the fourier expansion for [math]\displaystyle{ u_k }[/math] into (4):
Since [math]\displaystyle{ u_k }[/math] minimises J, we require [math]\displaystyle{ \frac{\partial J}{\partial a_{n}}=0 \quad \forall n }[/math]
[math]\displaystyle{ \frac{\partial J}{\partial a_{m}}=\int_{-L}^{L}\left\{2h\psi_m'\sum_{n=1}^{\infty} a_{n}\psi_n'-2\lambda\rho \psi_m \sum_{n=1}^{\infty} a_{n} \psi_n\right\}dx=0 }[/math]
[math]\displaystyle{ \implies \int_{-L}^{L}2h\psi_m'\sum_{n=1}^{\infty} a_{n}\psi_n'dx= \int_{-L}^{L}2\lambda\rho \psi_m \sum_{n=1}^{\infty} a_{n} \psi_ndx }[/math]
By defining a vector [math]\displaystyle{ \textbf{a} = \left(a_{n}\right) }[/math] and matrices [math]\displaystyle{ K_{(n,m)} = \int_{-L}^{L}h(x)\psi_m'(x)\psi_n'(x)dx }[/math] and [math]\displaystyle{ M_{(n,m)} = \int_{-L}^{L}\rho(x)\psi_m(x)\psi_n(x)dx }[/math] we have the linear system [math]\displaystyle{ K\textbf{a} = \lambda M\textbf{a} }[/math] which returns the eigenvalues and eigenvectors of equation (3), with eigenvectors [math]\displaystyle{ \textbf{a} }[/math] representing coefficient vectors of the fourier expansions of eigenfunctions.
If we now construct [math]\displaystyle{ u(x,\omega) = \sum_{k=1}^{\infty} b_k u_k }[/math] and substitute this into equation (2) we get
And defining the RHS of equation (5) as [math]\displaystyle{ f(x) }[/math], a known function, we can retrieve the coefficients [math]\displaystyle{ b_k }[/math] by integrating against [math]\displaystyle{ u_k }[/math]
[math]\displaystyle{ b_k = \frac{\int_{-L}^{L}\,f u_k\,dx}{(\omega^{2}-\lambda_k) \int_{-L}^{L}\, \rho u_{k}^{2}\,dx} }[/math]
The coefficients [math]\displaystyle{ c_n }[/math] of the fourier expansion of u are just [math]\displaystyle{ \sum_{k=1}^{\infty}a_{n,k}b_{k} }[/math] with [math]\displaystyle{ a_{n.k} }[/math] being the [math]\displaystyle{ n }[/math]th coefficient of the [math]\displaystyle{ k }[/math]th eigenfunction of the Sturm-Liouville problem.
So
with [math]\displaystyle{ \zeta |_{-L}=a \quad \zeta |_{L}=b }[/math] and, given [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math] explicitly differentiating [math]\displaystyle{ \zeta }[/math] gives [math]\displaystyle{ \partial_x \zeta |_{-L} }[/math] and [math]\displaystyle{ \partial_x \zeta |_L }[/math].
Matching at [math]\displaystyle{ \pm L }[/math]
We choose a basis of the solution space for any particular [math]\displaystyle{ \omega }[/math] to be [math]\displaystyle{ \{\zeta_1,\,\zeta_2\} }[/math], where [math]\displaystyle{ \zeta_1 }[/math] is the solution to the BVP(a=1,b=0) and [math]\displaystyle{ \zeta_1 }[/math] is the solution to the BVP(a=0,b=1). The functions [math]\displaystyle{ \zeta_1 }[/math] and [math]\displaystyle{ \zeta_2 }[/math] can be calculated for any [math]\displaystyle{ \omega }[/math] from (6).
The aim here is to construct a matrix S such that, given [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math]
[math]\displaystyle{ S \begin{pmatrix} \zeta |_{-L} \\ \zeta |_L \end{pmatrix}=\begin{pmatrix} \partial_x \zeta |_{-L} \\ \partial_x \zeta |_L \end{pmatrix} }[/math]
Taking [math]\displaystyle{ a=1,\,b=0 }[/math] to give [math]\displaystyle{ \zeta_1 }[/math] shows that the first column of S must be [math]\displaystyle{ \begin{pmatrix} \partial_x \zeta_1 |_{-L} \\ \partial_x \zeta_1 |_L \end{pmatrix} }[/math] and likewise taking [math]\displaystyle{ a=0,\,b=1 }[/math] to give [math]\displaystyle{ \zeta_2 }[/math] shows the second column must be [math]\displaystyle{ \begin{pmatrix} \partial_x \zeta_2 |_{-L} \\ \partial_x \zeta_2 |_L \end{pmatrix} }[/math]. So S is given by
[math]\displaystyle{ \begin{pmatrix} \partial_x \zeta_1 |_{-L} \, \partial_x \zeta_2 |_{-L} \\ \partial_x \zeta_1 |_L \, \partial_x \zeta_2 |_L \end{pmatrix} }[/math]
Now for the area of constant depth on the left hand side there is a potential of the form [math]\displaystyle{ e^{i\omega x} }[/math] which, creates reflected and transmitted potentials from the variable depth area of the form [math]\displaystyle{ Re^{-i\omega x} }[/math] and [math]\displaystyle{ Te^{i\omega x} }[/math] respectively where the magnitudes of [math]\displaystyle{ R }[/math] and [math]\displaystyle{ T }[/math] are unknown. We can calculate that the boundary conditions for [math]\displaystyle{ \zeta }[/math] must be
[math]\displaystyle{ \zeta |_{-L} = e^{-i\omega L}+Re^{i\omega L}, \quad \zeta |_L = Te^{i\omega L}, \quad \partial_x \zeta |_{-L} = i\omega e^{-i\omega L}-i\omega Re^{i\omega L}, \quad \partial_x \zeta |_L = i\omega Te^{i\omega L} }[/math]
[math]\displaystyle{ \begin{pmatrix} i\omega e^{-i\omega L}-i\omega Re^{i\omega L} \\ i\omega Te^{i\omega L} \end{pmatrix} = S\begin{pmatrix} e^{-i\omega L}+Re^{i\omega L} \\ Te^{i\omega L} \end{pmatrix} }[/math]
Knowing S these boundary conditions can be solved for [math]\displaystyle{ R }[/math] and [math]\displaystyle{ T }[/math], which in turn gives actual numerical boundary conditions to the original problem([math]\displaystyle{ a_+=e^{-i\omega L}+Re^{i\omega L} }[/math] and [math]\displaystyle{ b_+=Te^{i\omega L} }[/math]). Taking a linear combination of the solutions already calculated ([math]\displaystyle{ a_+\zeta_1(x,\omega) + b_+\zeta_2(x,\omega) }[/math]) will provide the solution for these new boundary conditions. This solution, along with the potentials outside this region gives a generalised eigenfunction potential for the whole real axis which we denote as [math]\displaystyle{ \zeta_+(x,\omega) }[/math].
Independent generalised eigenfunctons (which we denote as [math]\displaystyle{ \zeta_-(x,\omega) }[/math])can be found by considering the potential [math]\displaystyle{ e^{-i\omega x} }[/math] on the right hand region of constant depth. The corresponding reflected and transmitted potentials from the variable depth area are of the form [math]\displaystyle{ Re^{i\omega x} }[/math] and [math]\displaystyle{ Te^{-i\omega x} }[/math] respectively. Again knowing S we can solve for R and T and hence find the numerical boundary conditions ([math]\displaystyle{ a_-=Te^{i\omega L} }[/math] and [math]\displaystyle{ b_-=e^{-i\omega L}+Re^{i\omega L} }[/math]).
We come out with:
where R and T are found by solving:
and [math]\displaystyle{ a_+=e^{-i\omega L}+Re^{i\omega L} }[/math] and [math]\displaystyle{ b_+=Te^{i\omega L} }[/math]
Note that the values of R and T for [math]\displaystyle{ \zeta_- }[/math] are different from those for [math]\displaystyle{ \zeta_+ }[/math]
(although they are related through some identities). For [math]\displaystyle{ \zeta_- }[/math] we have:
where R and T are found by solving:
Note a_+, b_+, a_- and b_- are found frm their corresponding R and T values.
Generalised Eigenfunction Expansion
Now we have the generalised eigenfunctions [math]\displaystyle{ \zeta_+(x,\omega) }[/math] and [math]\displaystyle{ \zeta_-(x,\omega) }[/math], which have the orthogonality relationships:
For any particular [math]\displaystyle{ \omega }[/math] the general solution to the differential equation can be written as:
The general solution to the PDE is therefore:
Giving the initial conditions:
Using identities (7),(8) and (9) we can show:
Which we can use in combination with (10) to solve the IVP.
Matlab Code
Code to calculate the solution in a infinite basin can be found here infinite_basin_variable_h_and_rho.m