Wavemaker Theory

Introduction

Wavemaker

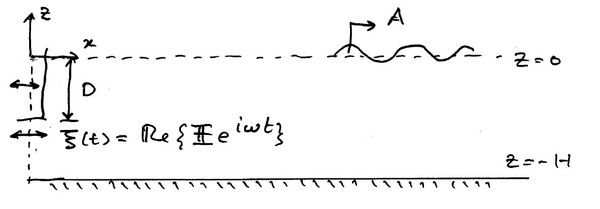
We will derive the potential in a two-dimensional wavetank due the motion of the wavemaker. The method is based on the Eigenfunction Matching Method. A paddle with draft [math]\displaystyle{ D\, }[/math] is undergoing small amplitude horizontal oscillations with displacement

[math]\displaystyle{ \xi (t) = \mathfrak{Re} \left \{ \Pi (Z) e^{i\omega t} \right \} }[/math]

where [math]\displaystyle{ \Pi\, }[/math] is assumed known and real. Because the oscillations are small the linear equations apply (which will be given formally below). This excitation creates plane progressive waves with amplitude [math]\displaystyle{ A \, }[/math] down the tank. The principal objective of wavemaker theory is to determine [math]\displaystyle{ A \, }[/math] as a function of [math]\displaystyle{ \omega, \Pi \, }[/math] and [math]\displaystyle{ H \, }[/math]. Time-dependent wavemaker theories can also be developed.

Expansion of the solution

In general, the wavemaker displacement at [math]\displaystyle{ X=0\, }[/math] may be written in the form

[math]\displaystyle{ \xi(t) = \mathfrak{Re} \left \{ \Pi (Z) e^{i\omega t} \right \} }[/math]

where [math]\displaystyle{ \Pi(Z) \, }[/math] is a known function of [math]\displaystyle{ Z \, }[/math]. The standard linear equations apply. Let the total velocity potential be

[math]\displaystyle{ \Phi = \mathfrak{Re} \left \{ \phi e^{i\omega t} \right \} }[/math]

where

[math]\displaystyle{ \phi = \phi_\omega \ + \psi }[/math]

The first term is a velocity potential that represents a Linear Plane Progressive Regular Wave down the tank with amplitude [math]\displaystyle{ A \, }[/math], yet unknown. Thus

[math]\displaystyle{ \phi_\omega = \frac{igA}{\omega} \frac{\cosh K (Z+H)}{\cosh KH} e^{-iKX + i\omega t} }[/math]

with [math]\displaystyle{ \omega^2 = gK \tanh KH. \, }[/math] (the Dispersion Relation for a Free Surface).

Evanescent modes and separation of variables

The second component potential [math]\displaystyle{ \psi\, }[/math] is by definition a decaying disturbance as [math]\displaystyle{ X \to \infty \, }[/math] and otherwise satisfies the following boundary value problem

[math]\displaystyle{ \begin{cases} \nabla^2 \psi = \psi_{XX} + \psi_{ZZ} = 0, -H \lt Z \lt 0 \\ \psi_Z - \frac{\omega^2}{g} \psi = 0, Z=0 \\ \psi_Z = 0, Z=-H \\ \psi \to 0, X \to \infty \end{cases} }[/math]

The condition on the wavemaker [math]\displaystyle{ (X=0) \, }[/math] is yet to be enforced. Note that unlike [math]\displaystyle{ \phi_\omega,\, \psi \, }[/math] does not representing a propagating wave down the tank so it is called a non-wavelike (evanescent) mode. Such modes do exist as will be shown below. On the wavemaker [math]\displaystyle{ (X=0) \, }[/math] the horizontal velocity due to [math]\displaystyle{ \phi_\omega\, }[/math] and that due to [math]\displaystyle{ \psi\, }[/math] must sum to the forcing velocity due to [math]\displaystyle{ \xi(t) \, }[/math].

When we solve Laplace's equation by separation of variables and apply the bottom boundary conditions we obtain solutions of the form [math]\displaystyle{ e^{-iKX} \cosh K(Z+H) }[/math] (which represent propagating waves and of the form [math]\displaystyle{ \cos \lambda (Z+H) \, }[/math]. Not that this solution satisfies the condition of vanishing value as [math]\displaystyle{ X \to \infty }[/math] provided that [math]\displaystyle{ \lambda \gt 0 \, }[/math]. These solutions satisfy Laplace's equation [math]\displaystyle{ \psi_{XX} + \psi_{ZZ} = 0, \, }[/math] for all [math]\displaystyle{ \lambda }[/math] and the seafloor condition : [math]\displaystyle{ \psi_Z = 0, Z=-H. }[/math] The free-surface condition implies that

[math]\displaystyle{ \psi_Z - \frac{\omega^2}{g} \psi = 0 \qquad \qquad \Longrightarrow \quad - \lambda \sin \lambda H - \frac{\omega^2}{g} \cos \lambda H = 0 }[/math] [math]\displaystyle{ \Longrightarrow \quad \lambda \tan \lambda H = - \nu \equiv \frac{\omega^2}{g} }[/math]

So for the non-wavelike modes [math]\displaystyle{ \psi, \lambda \, }[/math] must satisfy the Dispersion Relation for a Free Surface,

[math]\displaystyle{ \lambda \tan \lambda H = - \nu = - \frac{\omega^2}{g} \lt 0 }[/math]

For positive values of [math]\displaystyle{ \lambda \, }[/math] so that [math]\displaystyle{ e^{-\lambda X} \to 0, X \to + \infty \, }[/math]. Values of [math]\displaystyle{ \lambda_i \, }[/math] satisfying the dispersion relation follow from the solution of the non-dimensional nolinear equation

[math]\displaystyle{ \tan \omega = - \frac{\nu}{\omega}, \omega = \lambda H \, }[/math]

Solutions [math]\displaystyle{ \omega_i, i = 1, 2, \cdots \, }[/math] exist as shown above with [math]\displaystyle{ \omega_i \sim i \pi \, }[/math] for large [math]\displaystyle{ i \, }[/math]. These values are known as the eigenvalues or eigen-wavenumbers of the non-wavelike modes. The eigen-wavenumber of the wavelike solution [math]\displaystyle{ K\, }[/math] is given by the dispersion relation:

[math]\displaystyle{ \frac{\omega^2 H}{g} = KH \tan KH. \, }[/math]

It can easily be shown that setting [math]\displaystyle{ K = i \lambda \, }[/math], the dispersion relation of the non-wavelike nodes follows. In summary the purely imaginary roots of the surface wave dispersion relation and its single real positive root enter the solution of the wavemaker problem.

Orthogonal eigenfunctions

The solution of the for Dispersion Relation for a Free Surface leads to an infinite series of vertical eigenfunctions from Sturm-Liouville theory. This theory also shows that the eigenfunctions are orthogonal and we may define the following orthogonal eigenfunctions in the vertical direction [math]\displaystyle{ Z \, }[/math]:

[math]\displaystyle{ f_0 (Z) = \frac{\sqrt{2} \cosh K ( Z + H )}{{ (H + \frac{1}{v} \sinh^2 KH )}^{1/2}} }[/math] [math]\displaystyle{ f_n (Z) = \frac{\sqrt{2} \cosh \lambda_n ( Z + H )}{(H + \frac{1}{v} \sinh^2 \lambda_n H )}, \qquad n = 1, 2, \cdots }[/math]

Selected to satisfy:

[math]\displaystyle{ \begin{cases} \int_{-H}^0 f_0^2 (Z) dZ = \int_{-H}^0 f_n^2 (Z) dZ = 1 \\ \int_{-H}^0 f_m^2 (Z) f_n (Z) dZ = 0, \quad m \ne n \end{cases} }[/math]

So the wavemaker velocity potentials [math]\displaystyle{ \phi_w \, }[/math] and [math]\displaystyle{ \psi\, }[/math] can be expressed simply in terms of their respective eigen modes:

[math]\displaystyle{ \phi_w = a_0 f_0 (Z) e{-iKX} }[/math] [math]\displaystyle{ \psi = \sum_{n=1}^{\infty} a_n f_n (Z) e^{-\lambda_n X} }[/math]

and:

[math]\displaystyle{ \Phi = \mathfrak{Re} \left \{ ( \phi_w + \psi) e^{i\omega t} \right \} }[/math]

On [math]\displaystyle{ X=0 \, }[/math]:

[math]\displaystyle{ \Phi_X = \mathfrak{Re} \left \{ ( \phi_W + \psi_X)_X e^{i\omega t} \right \} }[/math] [math]\displaystyle{ \frac{d\xi}{dt} = \mathfrak{Re} \left \{ \Pi (Z) i \omega e^{i\omega t} \right \} }[/math]

Or:

[math]\displaystyle{ \frac{\partial}{\partial X} (\phi_W + \psi)_{X=0} = \Pi (Z) i \omega }[/math] [math]\displaystyle{ \left. \frac{\partial\phi_W}{\partial X} \right |_{X=0} = a_0 ( -iK) f_0 (Z) }[/math] [math]\displaystyle{ \left. \frac{\partial\psi}{\partial X} \right |_{X=0} = \sum_{n=1}^{\infty} a_n ( -\lambda_n) f_n (Z) }[/math]

It follows that:

[math]\displaystyle{ - i K a_0 f_0 (Z) + \sum_{n=1}^{\infty} a_n (- \lambda_n) f_n (Z) = i \omega \Pi (Z) }[/math]

Far Field Wave

One of the primary objecives of wavemaker theory is to determine [math]\displaystyle{ a_0 \, }[/math] (or the far-field wave amplitude [math]\displaystyle{ A \, }[/math] ) in terms of [math]\displaystyle{ \Pi (Z) \, }[/math]. Multiplying both sides by [math]\displaystyle{ f_0 (Z) \, }[/math], integrating from [math]\displaystyle{ - H \to 0 \, }[/math] and using orthogonality we obtain:

[math]\displaystyle{ - i K a_0 = i \omega \int_{-H}^0 dZ f_0 (Z) \Pi (Z) }[/math] [math]\displaystyle{ \Rightarrow \quad a_0 = - \frac{\omega}{K} \int_{-H}^0 dZ f_0 (Z) \Pi (Z) }[/math]

The far-field wave component representing progagating waves is given by:

[math]\displaystyle{ \phi_w = a_0 \frac{\sqrt{2} \cosh K (Z+H)}{{\left( H+\frac{1}{v} \sinh^2 KH \right)}^{1/2}} e^{-iKX} }[/math] [math]\displaystyle{ \equiv \frac{igA}{\omega} \frac{\cosh K (Z +H)}{\cosh KH} e^{-iKX} }[/math]

Plugging in [math]\displaystyle{ a_0\, }[/math] and solving for [math]\displaystyle{ A \, }[/math] we obtain the complex amplitude of the propagating wave at infinity, namely modulus and phase, in terms of the wave maker displacement [math]\displaystyle{ \Pi (Z) \, }[/math] and the other flow parameters.

---

This article is based on the MIT open course notes and the original article can be found here

Ocean Wave Interaction with Ships and Offshore Energy Systems