Multipole Expansions
Multipole expansions are a technique used in linear water wave theory where the potential is represented as a sum of singularities (multipoles) placed within any structures that are present. Multipoles can be constructed with their singularity submerged or on the free surface and these are treated separately.
Multipoles satisfy:
[math]\displaystyle{
\begin{align}
\Delta\phi &=0, &-h\lt z\lt 0,\,\,\mathbf{x} \in \Omega \\
\partial_z\phi &= 0, &z=-h, \\
\partial_z \phi &= \alpha \phi, &z=0,\,\,\mathbf{x} \in \partial \Omega_{\mathrm{F}},
\end{align}
}[/math]
(note that the last expression can be obtained from combining the expressions:
[math]\displaystyle{
\begin{align}
\partial_z \phi &= -\mathrm{i} \omega \zeta, &z=0,\,\,\mathbf{x} \in \partial \Omega_{\mathrm{F}}, \\
\mathrm{i} \omega \phi &= g\zeta, &z=0,\,\,\mathbf{x} \in \partial \Omega_{\mathrm{F}},
\end{align}
}[/math]
where [math]\displaystyle{ \alpha = \omega^2/g \, }[/math])
In two-dimensions the Sommerfeld Radiation Condition is
[math]\displaystyle{
\left( \frac{\partial}{\partial|x|} - \mathrm{i} k \right)
(\phi-\phi^{\mathrm{{I}}})=0,\;\mathrm{{as\;}}|x|\rightarrow\infty\mathrm{.}
}[/math]
where [math]\displaystyle{ \phi^{\mathrm{{I}}} }[/math] is the incident potential.
We consider here the theory only in two dimensions.
The multipoles are singular at a point [math]\displaystyle{ \mathbf{x^{\prime}} }[/math] and they have various orders of singularity.
For [math]\displaystyle{ n=0 }[/math]
[math]\displaystyle{ \phi_0 \to \ln r \,\mathrm{as}\, \mathbf{x} \to \mathbf{x}^{\prime} }[/math]
and for [math]\displaystyle{ n\gt 0 }[/math]
[math]\displaystyle{ \phi_n \to \frac{e^{in\theta}}{r^n} + \psi_n }[/math] as [math]\displaystyle{ \mathbf{x} \to \mathbf{x}^{\prime} }[/math]
where [math]\displaystyle{ (r,\theta) }[/math] are the polar coordinates centered at [math]\displaystyle{ \mathbf{x^{\prime}} }[/math]
A linear combination of these multipoles can then be made to satisfy the body boundary conditions.
Motivation for Multipoles
We present here the motivation for multipoles. For the case of Laplace's equation in an infinite
region surrounding a disk we may construct the solution very simply using a separation of variables
solution.
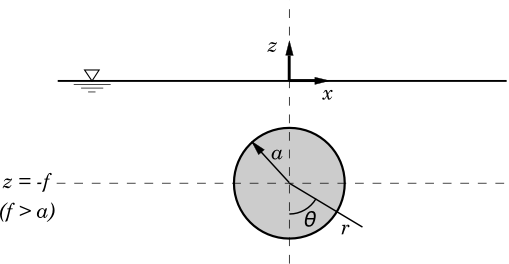
Consider Laplace's equation for
a disk of radius [math]\displaystyle{ a }[/math] (refer to Figure 1) centered at the origin in an infinite medium. The Laplace's equation in polar coordinates is
[math]\displaystyle{
\Delta \phi = \left[ \partial_r^2 + \frac{1}{r}\partial_r + \frac{1}{r^2} \partial_\theta^2 \right] \phi= 0 \quad
\mathrm{for} \quad r\gt a
}[/math]
We also have boundary conditions at the disk which we assume are Neumann given by
[math]\displaystyle{ \partial_n \phi |_{r=a} = 0
}[/math]
and we have a decay condition at infinity
[math]\displaystyle{
|\nabla\phi| \rightarrow 0 \quad \mathrm{as} \quad r \rightarrow \infty.
}[/math]
Using separation of variables
we write
[math]\displaystyle{ \phi(r,\theta) = R(r)\Theta(\theta).\, }[/math] Substituting into Laplace's equations gives
[math]\displaystyle{ \frac{r^2}{R}\partial_r^2 R + \frac{r}{R}\partial_r R = - \frac{1}{\Theta}\partial_\theta^2 \Theta = m^2
}[/math]
The equation for [math]\displaystyle{ \Theta\, }[/math] is
[math]\displaystyle{ \quad \frac{d^2\Theta}{d\theta^2} = -m^2\Theta }[/math]
[math]\displaystyle{ \Rightarrow \quad \Theta_m(\theta) = A_m \cos m\theta + B_m \sin m\theta \quad \mathrm{for} \quad m \gt 0 }[/math]
When [math]\displaystyle{ m=0\, }[/math] the solution is
[math]\displaystyle{ \Theta_0(\theta) = A_0 + B_0\theta, \quad \mathrm{we \ know \ that} \quad \Theta_0(0) = \Theta_0(2\pi) \, }[/math]
[math]\displaystyle{ A_0 = A_0 + B_02\pi \quad \therefore \quad B_0 = 0 \quad \mathrm{and} \quad \Theta_0(\theta) = A_0 \, }[/math]
The equation for [math]\displaystyle{ R\, }[/math] is
[math]\displaystyle{ \quad r^2\frac{d^2R}{dr^2} + r\frac{dR}{dr} = m^2 R \quad \mathrm{for} \quad m \gt 0 }[/math]
This is a standard differential equation, to solve we substitute [math]\displaystyle{ R(r)=r^n\, }[/math] giving:
[math]\displaystyle{ n(n-1)r^n + nr^n = m^2r^n \quad \Rightarrow \quad n^2 = m^2 \quad \Rightarrow \quad n= \pm m }[/math]
This gives two independent solutions for all [math]\displaystyle{ m\gt 0\, }[/math].
[math]\displaystyle{ \quad R_m(r) = C_m r^m + D_m r^{-m} }[/math]
Now
[math]\displaystyle{ r^2\frac{d^2R}{dr^2} + r\frac{dR}{dr} = 0 \quad \mathrm{for} \quad m = 0 }[/math]
[math]\displaystyle{ \Rightarrow \quad \frac{d}{dr} \left(r\frac{dR}{dr}\right) = 0, \quad \quad \frac{dR}{dr} = \frac{1}{r}D_0 }[/math]
So the solution for [math]\displaystyle{ m=0\, }[/math] is
[math]\displaystyle{ \quad R_0(r) = C_0 + D_0 \ln|r| }[/math]
The derivatives of the radial eigenfunctions must go to zero indicating zero fluid flow at infinity:
[math]\displaystyle{ |\nabla\phi| \rightarrow 0 \quad \mathrm{as} \quad r \rightarrow \infty \quad \quad \Rightarrow \quad \quad \frac{dR}{dr} \rightarrow 0 \quad \mathrm{as} \quad r \rightarrow \infty }[/math]
[math]\displaystyle{ \quad \frac{dR_m}{dr} = \frac{C_m m}{r}r^m - \frac{D_m m}{r}r^{-m} }[/math]
[math]\displaystyle{ C_m r^m - \frac{D_m}{r^m} \rightarrow 0 \quad \mathrm{as} \quad r \rightarrow \infty \quad \therefore \quad \mathrm{if} \quad m \gt 0 \quad \mathrm{then} \quad C_m = 0. }[/math]
[math]\displaystyle{ \quad R_m(r) = \frac{D_m}{r^m} }[/math]
Hence the general solution can be expressed as:
[math]\displaystyle{ \quad \phi(r,\theta) = R(r)\Theta(\theta) }[/math]
[math]\displaystyle{ \phi = R_0(r)\Theta_0(\theta) + \sum_{m=1}^\infty R_m(r)\Theta_m(\theta) }[/math]
[math]\displaystyle{ \phi = (C_0 + D_0 \ln r)A_0 + \sum_{m=1}^\infty \frac{D_m}{r^m}\left( A_m\cos m\theta + B_m\sin m\theta \right) }[/math]
[math]\displaystyle{ \phi = E_0 + F_0 \ln r + \sum_{m=1}^\infty \left( E_m\frac{\cos m\theta}{r^m} + F_m\frac{\sin m\theta}{r^m} \right) }[/math]
The solution can also be expressed simply in terms of complex exponentials.
[math]\displaystyle{ \phi(r,\theta) = E_0 + F_0 \ln r + \sum_{n=1}^\infty \left( G_n\frac{e^{in\theta}}{r^n} + H_n\frac{e^{-in\theta}}{r^n} \right) }[/math]
With the Free Surface Boundary Condition
When we introduce the free surface boundary condition we need to find a new set of eigenfunctions. We can use eigenfunctions from the infinite domain problem to construct them.
Here [math]\displaystyle{ r\, }[/math] and [math]\displaystyle{ \theta\, }[/math] are polar coordinates defined by [math]\displaystyle{ z + f = -r\cos\theta\, }[/math], [math]\displaystyle{ \quad \, }[/math] [math]\displaystyle{ x = r\sin\theta \, }[/math], note also that the origin is in the free surface directly above the center of the disc for cartesian coordinates. However the origin for the polar coordinates is still at the center of the disk, as shown in Figure 1.
We add a solution of Laplace's equation to the eigenfunctions for the infinite domain problem and require that these new functions (multipoles) satisfy the free surface condition.
For [math]\displaystyle{ n\gt 0\, }[/math]
[math]\displaystyle{ \phi_n = \frac{e^{in\theta}}{r^n} + \psi_n }[/math]
and for [math]\displaystyle{ n=0\, }[/math]
[math]\displaystyle{ \phi_0 = \ln r + \psi_0 \, }[/math]
Where
[math]\displaystyle{ \Delta \psi_n = 0 \quad \mathrm{for} \quad n = 0,1,2, \ldots }[/math]
We want the multipoles to satisfy the free surface condition
[math]\displaystyle{ \partial_z \phi_n |_{z=0} = k\phi_n|_{z=0} \quad \forall \ n = 0,1,2, \ldots }[/math]
For [math]\displaystyle{ n=0\, }[/math] the free surface condition gives our boundary condition for [math]\displaystyle{ \psi_0\, }[/math]:
[math]\displaystyle{ f_0(x) = (\partial_z - k)\psi_0|_{z=0} = (k - \partial_z) \ln\left(\frac{r}{a}\right)|_{z=0} }[/math]
[math]\displaystyle{ = k \ln\left(\frac{\sqrt{x^2 + f^2}}{a}\right) - \int_0^\infty \mu e^{-\mu f}\cos\mu x \ d\mu \quad \quad \quad \quad \quad \quad (1) }[/math]
where we used the following integral representation of the singularity (see Ref.)
[math]\displaystyle{ \ln r = \int_0^\infty (e^{-\mu}- e^{-\mu|z+f|}\cos\mu x)\frac{d\mu}{\mu} \quad \quad \quad \quad \quad \quad (2) }[/math]
The singularity at [math]\displaystyle{ (0,-f)\, }[/math] (refer to Figure 1) is not of the form [math]\displaystyle{ \ln r\, }[/math] since this would give a potential that corresponds to a pulsating source of fluid. From this point on Multipoles with higher order with a submerged singularity are only considered for this problem
For [math]\displaystyle{ n\gt 0\, }[/math] the free surface condition yields the boundary condition for [math]\displaystyle{ \psi_n\, }[/math]:
[math]\displaystyle{ f_n(x) = (\partial_z - k)\psi_n|_{z=0} = \left(k - \partial_z \right) \left(\frac{e^{in\theta}}{r^n}\right)|_{z=0} }[/math]
[math]\displaystyle{ = \frac{(-1)^n}{(n-1)!} \int_0^\infty(k+\mu)\mu^{n-1}e^{-\mu f}e^{-i\mu x} d\mu \quad \quad \quad \quad \quad \quad (3) }[/math]
where we used the following integral representation of the singularity (see Ref.) (valid for [math]\displaystyle{ z\gt -f\, }[/math])
[math]\displaystyle{ \frac{e^{in\theta}}{r^n} = \frac{(-1)^n}{(n-1)!} \int_0^\infty\mu^{n-1}e^{-\mu(z+f) }e^{-i\mu x} d\mu \quad \quad \quad \quad \quad \quad (4) }[/math]
The [math]\displaystyle{ \psi_n(x,z)\, }[/math] functions now satisfy the following problem:
[math]\displaystyle{ \Delta \psi_n = 0 \quad \mathrm{for} \quad n = 0,1,2, \ldots }[/math]
[math]\displaystyle{ \partial_z\psi_n \rightarrow 0 \quad \mathrm{as} \quad z \rightarrow -\infty }[/math]
[math]\displaystyle{ \partial_z \psi_n |_{z=0} - k\psi_n|_{z=0} = f_n(x) }[/math]
We solve for [math]\displaystyle{ \hat{\psi}_n\, }[/math] by taking a Fourier transform in [math]\displaystyle{ x\, }[/math] to simplify Laplace's equation
[math]\displaystyle{ \hat{\psi}_n(\mu,z) = \int_{-\infty}^\infty \psi_n(x,z) e^{i\mu x}dx }[/math]
After applying the Fourier transform we have
[math]\displaystyle{ \partial_z^2 \hat{\psi}_n - \mu^2\hat{\psi}_n = 0 }[/math]
The solution of this equation is
[math]\displaystyle{ \hat{\psi}_n = A_n(\mu)e^{|\mu| z} + B_n(\mu)e^{-|\mu| z} }[/math]
After applying the boundary condition at
[math]\displaystyle{ z \rightarrow -\infty \quad \Rightarrow \quad B_n(\mu) = 0 \quad \forall \ n }[/math]
We apply the Fourier transform to the surface boundary condition
[math]\displaystyle{ \partial_z \hat{\psi}_n |_{z=0} - k\hat{\psi}_n|_{z=0} = \hat{f}_n(\mu) }[/math]
[math]\displaystyle{ A_n(\mu)|\mu| - k A_n(\mu) = \hat{f}_n(\mu), \quad A_n(\mu) = \frac{\hat{f}_n(\mu)}{|\mu| - k}, \quad \hat{\psi}_n(\mu,z) = \frac{\hat{f}_n(\mu)}{|\mu| - k}e^{|\mu|z} }[/math]
we can obtain [math]\displaystyle{ \psi_n\, }[/math] by the inverse Fourier transform
[math]\displaystyle{ \psi_n(x,z) = \frac{1}{2\pi}\int_{-\infty}^\infty \hat{\psi}_n(\mu,z) e^{-i\mu x}d\mu \quad \quad = \frac{1}{2\pi}\int_{-\infty}^\infty \frac{\hat{f}_n(|\mu|)}{|\mu| - k} e^{|\mu| z} e^{-i\mu x}d\mu \quad \quad \quad \quad \quad \quad (5) }[/math]
For [math]\displaystyle{ n\gt 0\, }[/math] the form of [math]\displaystyle{ \hat{f}_n(|\mu|) }[/math] can be obtained from [math]\displaystyle{ f_n(x)\, }[/math] [math]\displaystyle{ (3)\, }[/math] by rewriting it as a Fourier transform. Refer to Appendix A2 for confirmation that changing the limits of integration with different constant outside of integration for [math]\displaystyle{ \psi_n(x,z)\, }[/math] gives the same result. Now substituting the result into [math]\displaystyle{ (5)\, }[/math], [math]\displaystyle{ \psi_n\, }[/math] easily simplifies to:
[math]\displaystyle{ \psi_n(x,z) = \frac{(-1)^n}{(n-1)!} \int_0^\infty \frac{\mu + k}{\mu - k} \mu^{n-1} e^{\mu (z-f)} e^{-i\mu x}d\mu \quad \quad \quad \quad \quad \quad (6) }[/math]
Note: the integral is singular at [math]\displaystyle{ \mu=k\, }[/math].
[math]\displaystyle{ \psi_n(x,z)\, }[/math] can be expanded in a power series:
[math]\displaystyle{ \psi_n(r,\theta) = \sum_{m=0}^\infty A_{mn}r^m e^{im\theta} \quad \textrm{for} \quad n\gt 0 }[/math]
where
[math]\displaystyle{ A_{mn}= \frac{(-1)^{m+n}}{m!(n-1)!} \int_0^\infty \frac{\mu + k}{\mu - k} \mu^{m+n-1} e^{-2\mu f} d\mu \quad \quad \quad \quad \quad \quad (7) }[/math]
Note: the integral is singular at [math]\displaystyle{ \mu=k\, }[/math]. Refer to Appendix A1 on steps required to numerically integrate this singular integral.
This result is arrived at by expanding the exponential part of the integral of [math]\displaystyle{ \psi_n(x,z)\, }[/math]. So we have
[math]\displaystyle{ \quad = e^{\mu(z-f) -i\mu x} }[/math]
[math]\displaystyle{ \quad = e^{\mu[(-f - r \cos\theta-f) - i r \sin\theta]} }[/math]
[math]\displaystyle{ = e^{-2\mu f}e^{-\mu r e^{i\theta}} }[/math]
[math]\displaystyle{ = e^{-2\mu f}\sum_{m=0}^\infty \frac{(-1)^m}{m!} \mu^m r^m e^{im\theta} }[/math]
This identity is then substituted into the expression for [math]\displaystyle{ \psi_n\, }[/math] to complete the power series.
In order to have a complete set to expand our fluid potential we need to include [math]\displaystyle{ \bar{\phi}_n \, }[/math] for [math]\displaystyle{ n\gt 0 \, }[/math].
This accounts for the second linearly independent solution for [math]\displaystyle{ n\gt 0 \, }[/math].
Wave-Free Potentials
The combination [math]\displaystyle{ \phi_{n+1}(x,z) + kn^{-1}\phi_n(x,z)\, }[/math], [math]\displaystyle{ n=1,2,3,...\, }[/math] corresponds to a wave free singularity i.e. no waves are radiated to infinity so the potential dies off in the far field.
[math]\displaystyle{ \phi_{n+1} \ + \ kn^{-1}\phi_n = \left(\frac{e^{i(n+1)\theta}}{r^{(n+1)}} + \frac{(-1)^{(n+1)}}{n!} \int_0^\infty \frac{\mu + k}{\mu - k} \mu^{n} e^{\mu (z-f)} e^{-i\mu x}d\mu \right) \ + \ \frac{k}{n}\left( \frac{e^{in\theta}}{r^n} + \psi_n(x,z) \right) \quad \quad \quad \quad \quad \quad (12) }[/math]
where [math]\displaystyle{ \psi_n(x,z) \, }[/math] is defined by [math]\displaystyle{ (6)\, }[/math].
The above relationship can be simplified by using the coordinate relationships defined below. The coordinates that are use are illustrated in Figure 2.
[math]\displaystyle{ r = \sqrt{x^2 + (z+f)^2}, \quad r_1 = \sqrt{x^2 + (z-f)^2}, }[/math]
[math]\displaystyle{ x = r \sin \theta = r_1 \sin \theta_1,\, }[/math]
[math]\displaystyle{ -z-f = r \cos \theta, \quad z-f = r_1 \cos \theta_1. }[/math]
Resulting in the expression:
[math]\displaystyle{ \phi_{n+1}(r,\theta) + kn^{-1}\phi_n(r,\theta) = \frac{e^{i(n+1)\theta}}{r^{(n+1)}} + \frac{k}{n}\frac{e^{in\theta}}{r^n} + \frac{e^{-i(n+1)\theta_1}}{r_1^{(n+1)}} - \frac{k}{n}\frac{e^{-in\theta_1}}{r_1^n} }[/math]
i.e.
[math]\displaystyle{ \phi_{n+1} + kn^{-1}\phi_n = \left( \frac{e^{i(n+1)\theta}}{r^{(n+1)}} + \frac{e^{-i(n+1)\theta_1}}{r_1^{(n+1)}} \right) + \frac{k}{n} \left( \frac{e^{in\theta}}{r^n} - \frac{e^{-in\theta_1}}{r_1^n} \right) \quad \quad \quad \quad \quad \quad (13) }[/math]
Once again to obtain a complete set we also use the complex conjugates of these potentials.
Example: 2D Wave Scattering for a Submerged Horizontal Cylinder (in Infinite Depth)
- Picture to show problem set up***
The potential for the scattering problem splits as incident and diffracted potentials and also into symmetric and antisymmetric parts.
[math]\displaystyle{ \phi = \phi_I + \phi_D \, }[/math]
[math]\displaystyle{ = (\phi^s_I + \phi^a_I) + (\phi^s_D + \phi^a_D) }[/math]
[math]\displaystyle{ = (\phi^s_I + \phi^s_D) + (\phi^a_I + \phi^a_D) }[/math]
[math]\displaystyle{ = \phi^s + \phi^a \, }[/math]
where
[math]\displaystyle{ \partial_n \phi |_{r=a} = 0 \quad \Rightarrow \quad \partial_r \phi_I |_{r=a} = - \partial_r \phi_D |_{r=a} }[/math]
and [math]\displaystyle{ \phi^s, \,\, \phi^a }[/math] are the symmetric and antisymmetric parts of [math]\displaystyle{ \phi \, }[/math] respectively.
For a wave incident from the left we have where [math]\displaystyle{ k = \frac{\omega^2}{g} \, }[/math]
[math]\displaystyle{ \phi_I = e^{kz} e^{ikx} = e^{-kf}\sum_{n=0}^\infty \frac{(-kr)^n }{n!} e^{-in\theta} }[/math]
[math]\displaystyle{ = e^{-kf}\sum_{n=0}^\infty \frac{(-kr)^n }{n!} \cos n\theta + ie^{-kf}\sum_{n=0}^\infty \frac{(-kr)^n }{n!} \sin n\theta }[/math]
[math]\displaystyle{ = \phi^s_I + \phi^a_I \, }[/math]
[math]\displaystyle{ \phi_D = \sum_{n=1}^{\infty}a^n \alpha_n \phi_n^s + \sum_{n=1}^{\infty}a^n \beta_n \phi_n^a }[/math]
[math]\displaystyle{ = \phi^s_D + \phi^a_D \, }[/math]
[math]\displaystyle{ \phi^s(r,\theta) = e^{-kf}\sum_{n=0}^\infty \frac{(-kr)^n }{n!} \cos n\theta + \sum_{n=1}^{\infty}a^n \alpha_n \left(\frac{\cos n\theta}{r^n} + \sum_{m=0}^\infty A_{mn}^+ r^m \cos m\theta\right) \quad \quad \quad \quad \quad \quad (8) }[/math]
[math]\displaystyle{ \phi^a(r,\theta) = ie^{-kf}\sum_{n=0}^\infty \frac{(-kr)^n }{n!} \sin n\theta + \sum_{n=1}^{\infty}a^n \beta_n \left(\frac{\sin n\theta}{r^n} + \sum_{m=0}^\infty A_{mn}^- r^m \sin m\theta\right) \quad \quad \quad \quad \quad \quad (9) }[/math]
The above power series converge for [math]\displaystyle{ r \lt 2f \, }[/math] where [math]\displaystyle{ A^+_{mn} \, }[/math] and [math]\displaystyle{ A^-_{mn} \, }[/math] are both defined by [math]\displaystyle{ (7)\, }[/math].
Applying the body boundary condition [math]\displaystyle{ \partial_r \phi^{s,a} |_{r=a} = 0 }[/math] and noting that the cosines are orthogonal over [math]\displaystyle{ \theta \in (-\pi,\pi] }[/math] gives the results
[math]\displaystyle{ \alpha_m - \sum_{n=1}^{\infty}a^{n+m} A^+_{mn} \alpha_n = e^{-kf}\frac {(-ka)^m}{m!}; \quad m=1,2,3,\ldots \quad \quad \quad \quad \quad \quad (10) }[/math]
[math]\displaystyle{ \beta_m - \sum_{n=1}^{\infty}a^{n+m} A^-_{mn} \beta_n = -ie^{-kf}\frac {(-ka)^m}{m!}; \quad m=1,2,3,\ldots }[/math]
From which we can see that [math]\displaystyle{ \beta_n = -i\alpha_n\, }[/math].
The above sums can be truncated at the Nth term yielding NxN system of linear equations that can be solved for the coefficients [math]\displaystyle{ \alpha_n\, }[/math]
Hence we can calculate [math]\displaystyle{ \phi\, }[/math] from:
[math]\displaystyle{ \phi = \phi^s + \phi^a = \phi_I + \sum_{n=1}^{\infty}a^n \alpha_n ( \phi^s_n - i\phi^a_n ) \quad \quad \quad \quad \quad \quad (11) }[/math]
This expression also gives the values of the reflection and transmission coefficients when we substitute the far field expressions for the symmetric and antisymmetric multipoles.
In the far field:
[math]\displaystyle{ \phi^s_n(x,z) \sim \frac{2\pi i (-k)^n}{(n-1)!} e^{k(z-f)} e^{\pm ikx} \quad \mathrm{as} \quad x \rightarrow \pm \infty }[/math]
[math]\displaystyle{ \phi^a_n(x,z) \sim \mp \frac{2\pi (-k)^n}{(n-1)!} e^{k(z-f)} e^{\pm ikx} \quad \mathrm{as} \quad x \rightarrow \pm \infty }[/math]
Giving:
[math]\displaystyle{ R=0, \quad T = 1 + 4 \pi i e^{-kf} \sum_{n=1}^{\infty} \alpha_n \frac{(-ka)^n}{(n-1)!} }[/math]
Hydrodynamic Forces
Soon will write something here
Appendix A
Appendix A1
The coefficients [math]\displaystyle{ A_{mn}\, }[/math] are evaluated by the following singular integral:
[math]\displaystyle{ A_{mn} = \frac{(-1)^{m+n}}{m!(n-1)!} \int_{0}^\infty \frac{\mu + k}{\mu - k} \mu^{m+n-1} e^{-2\mu f} \ d \mu }[/math]
To evaluate this singular integral numerically we separate into less onerous components. If we let
[math]\displaystyle{ A_{mn} = \frac{(-1)^{m+n}}{m!(n-1)!} \int_{0}^\infty \frac{h(\mu)}{\mu - k} e^{-2\mu f} \ d \mu \quad \quad \mathrm{where} \quad \quad h(\mu) = (\mu+k)\mu^{m+n-1} }[/math]
and if we let [math]\displaystyle{ \xi = 2\mu f \, }[/math] it follows that [math]\displaystyle{ d \xi = 2fd \mu \, }[/math], then
[math]\displaystyle{ A_{mn} = \frac{(-1)^{m+n}}{m!(n-1)!} \int_{0}^\infty \frac{h(\frac{\xi}{2f})}{\frac{\xi}{2f} - k} e^{-\xi} \ \frac{d \xi}{2f} }[/math]
[math]\displaystyle{ = \frac{(-1)^{m+n}}{m!(n-1)!} \left( \frac{1}{2f} \int_{0}^\infty \frac{h(\frac{\xi}{2f})-h(k)}{\frac{\xi}{2f} - k} e^{-\xi} \ d \xi + \frac{1}{2f} \int_{0}^\infty \frac{h(k)}{\frac{\xi}{2f} - k} e^{-\xi} \ d \xi\right) }[/math]
[math]\displaystyle{
= \frac{(-1)^{m+n}}{m!(n-1)!} \left(\int_{0}^\infty \frac{h(\frac{\xi}{2f})-h(k)}{\xi - \upsilon} e^{-\xi} \ d \xi + h(k) \int_{0}^\infty \frac{e^{-\xi}}{\xi - \upsilon} \ d \xi\right) \quad \quad \mathrm{where} \quad \quad \upsilon = 2fk }[/math]
The first integral is no longer singular and can be numerically evaluated using an adaptive Gauss-Kronrod quadrature. The second integral remains singular and can be transformed into a series of known functions as follows:
[math]\displaystyle{ h(k) \int_{0}^\infty \frac{e^{-\xi}}{\xi - \upsilon} \ d \xi\ = \ h(k) \left[f(\upsilon) + i\pi e^{-\upsilon} \right] \quad \quad \mathrm{where} \quad \quad f(\upsilon) = \int_{0}^\infty \frac{e^{-\xi}}{\xi - \upsilon} \ d \xi }[/math]
now if we let [math]\displaystyle{ t = -\xi + \upsilon \, }[/math] it follows that [math]\displaystyle{ dt = -d \xi \, }[/math]. The limits of integration follow suit, at [math]\displaystyle{ \xi = 0 \, }[/math] [math]\displaystyle{ t = \upsilon \, }[/math] and at [math]\displaystyle{ \xi = \infty \, }[/math] [math]\displaystyle{ t = -\infty \, }[/math].
[math]\displaystyle{ = h(k) \left( \int_{\upsilon}^{-\infty} \frac{e^{t-\upsilon}}{-t} \ (-d t) + i\pi e^{-\upsilon} \right) }[/math]
[math]\displaystyle{ = h(k) \left(e^{-\upsilon} \int_{\upsilon}^{-\infty} \frac{e^{t}}{t} \ d t + i\pi e^{-\upsilon} \right) }[/math]
[math]\displaystyle{ = h(k) \left(-e^{-\upsilon} \int_{-\infty}^{\upsilon} \frac{e^{t}}{t} \ d t + i\pi e^{-\upsilon} \right) }[/math]
[math]\displaystyle{ = h(k) \left[-e^{-\upsilon} Ei(\upsilon) \ + \ i\pi e^{-\upsilon} \right] \quad \quad \mathrm{where} \quad \quad Ei(\upsilon) \quad \mathrm{is \ the \ Cauchy \ principal \ value \ of \ the \ integral} }[/math]
[math]\displaystyle{ = h(k) \left\{e^{-\upsilon} [E_1(-\upsilon) + i\pi] + i\pi e^{-\upsilon} \right\} \quad \quad \mathrm{where} \quad \quad E_1(\upsilon) \quad \mathrm{is \ the \ Exponential \ integral} }[/math]
Therefore
[math]\displaystyle{ A_{mn} = \frac{(-1)^{m+n}}{m!(n-1)!} \left\{\int_{0}^\infty \frac{h(\frac{\xi}{2f}) - h(k)}{\xi - \upsilon} e^{-\xi} \ d \xi + h(k)e^{-\upsilon} \left[E_1(-\upsilon) + 2i\pi \right] \right\} \quad \mbox{ where } }[/math]
[math]\displaystyle{ h(\frac{\xi}{2f}) = (\frac{\xi}{2f}+k)(\frac{\xi}{2f})^{m+n-1} }[/math]
Appendix A2
We can write:
[math]\displaystyle{ f_n(x) = \int_0^\infty g_n(\mu)e^{-i\mu x} d\mu \quad \quad \textrm{where} \quad g_n(\mu)= \frac{(-1)^n}{(n-1)!}(\mu+k)\mu^{n-1}e^{-\mu f} }[/math]
We can rewrite [math]\displaystyle{ f_n(x)\, }[/math] as an inverse Fourier transform by using the Euler identity and the odd and even properties of sine and cosine. Allowing us to obtain [math]\displaystyle{ \hat{f}_n(\mu)\, }[/math]:
[math]\displaystyle{ f_n(x) = \int_0^\infty g_n(\mu)\cos\mu x \ d\mu -i \int_0^\infty g_n(\mu)\sin\mu x \ d\mu }[/math]
[math]\displaystyle{ = \frac{1}{2}\int_{-\infty}^\infty g_n(|\mu|)\cos\mu x \ d\mu -\frac{i}{2} \int_{-\infty}^\infty \frac{\mu}{|\mu|}g_n(|\mu|)\sin\mu x \ d\mu }[/math]
Since [math]\displaystyle{ g_n(|\mu|)\, }[/math] is even, its integral against sine over all [math]\displaystyle{ x\, }[/math] is zero so we can replace the cosine with a complex exponential in the first integral (similarly we replace (-i sine) for the second).
[math]\displaystyle{ f_n(x) = \frac{1}{2}\int_{-\infty}^\infty g_n(|\mu|)e^{-i\mu x} d\mu + \frac{1}{2} \int_{-\infty}^\infty sgn(\mu)g_n(|\mu|)e^{-i\mu x} d\mu }[/math]
Finally, combining the integrals, [math]\displaystyle{ \hat{f}_n(\mu) }[/math] emerges:
[math]\displaystyle{ f_n(x) = \int_{-\infty}^\infty \frac{1}{2}\left[ g_n(|\mu|) + sgn(\mu)g_n(|\mu|)\right] e^{-i\mu x} d\mu \quad = \int_0^\infty g_n(\mu)e^{-i\mu x} d\mu }[/math]
and so these two integrals are equivalent
[math]\displaystyle{ \psi_n(x,z) = \frac{1}{2\pi}\int_{-\infty}^\infty \ldots \quad , \quad \psi_n(x,z) = \int_0^\infty \ldots }[/math]