Category:Symmetry in Two Dimensions
Introduction
If we consider the problem of an incident wave from the left on a body, or group of bodies, which are symmetric about [math]\displaystyle{ x=0 }[/math] then we can decompose the problem into an symmetric and anti-symmetric problem. The first problem can be thought of as having Neuman boundary conditions at [math]\displaystyle{ x=0 }[/math] and the second as having Dirichlet boundary conditions at [math]\displaystyle{ x=0 }[/math]. The solution to the original problem is then found by adding these two problems together thanks to the superposition principle.
Original Problem
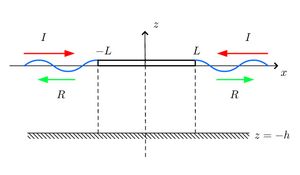
We consider here a body or a group of bodies which are geometrically symmetric about [math]\displaystyle{ x=0 }[/math]. An incident wave coming from the left will be reflected on the left and transmitted on the right side of the domain. The body extend up to [math]\displaystyle{ |x|=L }[/math] (where we will place a matching boundary) and the finite depth [math]\displaystyle{ h }[/math].
Symmetric solution
We consider here a solution where the potential and the corresponding velocity is symmetric about the plane [math]\displaystyle{ x=0 }[/math]. The symmetric problem consists of two identical incident waves coming from each side of the symmetric body. Their horizontal spatial dependence is respectively [math]\displaystyle{ \exp\,(-k_{0}(x+L)) }[/math] and [math]\displaystyle{ \exp\,(k_{0}(x-L)) }[/math] and they have both unit amplitude and same phase. Two waves are emitted at the edges of the body and propagate away from it on each side, again with the same amplitude and phase.
The symmetry of velocity field implies that the normal velocity is zero on the symmetry plane at [math]\displaystyle{ x=0 }[/math]. We need to solve the problem on the plane [math]\displaystyle{ x\lt 0 }[/math] only and then we can build the solution on the other plane simply by symmetry.
The symmetric solution on the left half plane can now be obtained from the solution with a semi-infinite body. To that extent, we first translate horizontally the origin for the open-water region and we write the symmetric potential [math]\displaystyle{ \, \phi_s }[/math] as
[math]\displaystyle{ \phi_s(x,z)=e^{-k_{0}(x+L)}\phi_{0}\left( z\right) + \sum_{m=0}^{\infty}a_{m}e^{k_{m}(x+L)}\phi_{m}(z), \;\;x\lt -L }[/math]
In the region under the body, for [math]\displaystyle{ -L\lt x\lt 0 }[/math], the potential satisfies a Neumann condition at [math]\displaystyle{ x=0 }[/math]. This will change the modes of the semi-infinite solution into some even functions of [math]\displaystyle{ x }[/math].
The matching conditions lead to a set of equations very similar to the semi-infinite one.
Anti-symmetric solution
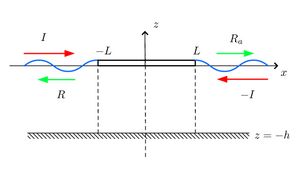
We consider now a solution where the corresponding velocity is anti-symmetric about the plane [math]\displaystyle{ x=0 }[/math]. Or equivalently the potential is an odd function of the horizontal direction. The anti-symmetric problem consists of two incident waves coming from each side of the symmetric body, with the same amplitude but out of phase. Their horizontal spatial dependence is respectively [math]\displaystyle{ \exp\,(-k_{0}(x+L)) }[/math] and [math]\displaystyle{ -\exp\,(k_{0}(x-L)) }[/math]. Two waves are emitted at the edges of the body and propagate away from it on each side, again out of phase.
The fact that the potential is odd field implies that it is equal to zero on the symmetry plane at [math]\displaystyle{ x=0 }[/math]. We need to solve the problem on the plane [math]\displaystyle{ x\lt 0 }[/math] only and then we can build the solution on the other plane simply by anti-symmetry.
The anti-symmetric solution on the left half plane can here also be obtained from the solution with a semi-infinite body. The potential in the open-water region is identical as the one in the symmetric solution.
In the region under the body, for [math]\displaystyle{ -L\lt x\lt 0 }[/math], the anti-symmetric potential [math]\displaystyle{ \, \phi_a }[/math] now satisfies a Dirichlet condition at [math]\displaystyle{ x=0 }[/math]. This again changes the modes of the semi-infinite solution into odd functions of [math]\displaystyle{ x }[/math].
The matching conditions lead to a set of equations very similar to the semi-infinite one.
Solution to the original problem
The solution for the symmetric body with an incident wave coming from the left can be evaluated from the previous symmetric and anti-symmetric solutions by using the principle of superposition. The velocity potential in the left open-water region, for [math]\displaystyle{ x\lt 0 }[/math], is simply
[math]\displaystyle{ \phi(x,z) = \frac{1}{2} \left( \phi_s(x,z) + \phi_a(x,z) \right) }[/math]
whereas in the right-open water region, for [math]\displaystyle{ x\gt 0 }[/math]
[math]\displaystyle{ \phi(x,z) = \frac{1}{2} \left( \phi_s(x,z) + \phi_a(x,z) \right) = \frac{1}{2} \left( \phi_s(-x,z) - \phi_a(-x,z) \right) }[/math]
In the last expression, the first equality comes from the superposition principle and the second one is obtained considering that the symmetric potential is an even function of [math]\displaystyle{ x }[/math] whereas the anti-symmetric potential is an odd function.
Application
This theory of symmetry is used for the case of a finite dock (see Eigenfunction Matching for a Finite Dock), for two identical docks (see Two Identical Docks using Symmetry)
Pages in category "Symmetry in Two Dimensions"
The following 4 pages are in this category, out of 4 total.