Green Function Method for a Finite Dock
Introduction
The problem of a two-dimensional finite dock is solved using a green function. The same problem is solved using eigenfunction matching in Eigenfunction Matching for a Finite Dock. The problem of a floating body on the surface using the same method is treated in Green Function Method for a Floating Body on the Surface and for a floating elastic plate in Green Function Methods for Floating Elastic Plates
Equations for a Dock in the Frequency Domain
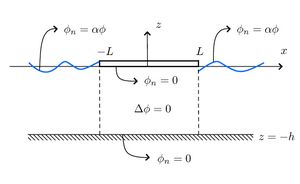
We consider here the Frequency Domain Problem for a finite dock which occupies the region [math]\displaystyle{ -L\lt x\lt L }[/math] (we assume [math]\displaystyle{ e^{i\omega t} }[/math] time dependence). The water is assumed to have constant finite depth [math]\displaystyle{ h }[/math] and the [math]\displaystyle{ z }[/math]-direction points vertically upward with the water surface at [math]\displaystyle{ z=0 }[/math] and the sea floor at [math]\displaystyle{ z=-h }[/math]. The boundary value problem can therefore be expressed as
[math]\displaystyle{ \Delta\phi=0, \,\, -h\lt z\lt 0, }[/math]
[math]\displaystyle{ \phi_{z}=0, \,\, z=-h, }[/math]
[math]\displaystyle{ \partial_z\phi=0, \,\, z=0,\,-L\lt x\lt L, }[/math]
We must also apply the Sommerfeld Radiation Condition as [math]\displaystyle{ |x|\rightarrow\infty }[/math]. This essentially implies that the only wave at infinity is propagating away and at negative infinity there is a unit incident wave and a wave propagating away.
We begin with the diffraction potential [math]\displaystyle{ \phi^{\mathrm{D}} }[/math] which satisfies the following equations
[math]\displaystyle{ \phi^{\mathrm{D}} }[/math] satisfies the Sommerfeld Radiation Condition
[math]\displaystyle{ \phi^{\mathrm{I}}\, }[/math] is a plane wave travelling in the [math]\displaystyle{ x }[/math] direction,
where [math]\displaystyle{ A }[/math] is the wave amplitude (in potential) [math]\displaystyle{ \mathrm{i} k }[/math] is the positive imaginary solution of the Dispersion Relation for a Free Surface (note we are assuming that the time dependence is of the form [math]\displaystyle{ \exp(-\mathrm{i}\omega t) }[/math]) and
As the plate is floating on the surface, we can denote it as follows:
Solution for Diffracted Potential
We use the Free-Surface Green Function for two-dimensional waves, with singularity at the water surface since we are only interested in its value at [math]\displaystyle{ z=0 }[/math] (details about this method can be found in Integral Equation for the Finite Depth Green Function at Surface). Using this we can transform the system of equations to
Reflection and Transmission Coefficients
The Reflection and Transmission Coefficients represent the ratio of the amplitude of the reflected or transmitted wave to the amplitude of the incident wave. Conservation of energy means that [math]\displaystyle{ |R|^2+|T|^2=1\, }[/math].
We can calculate the Reflection and Transmission coefficients by applying Green's theorem to [math]\displaystyle{ \phi\, }[/math] and [math]\displaystyle{ \phi^{\mathrm{I}}\, }[/math] [math]\displaystyle{ \phi^{\mathrm{I}}\, }[/math] is a plane wave travelling in the [math]\displaystyle{ x }[/math] direction,
where [math]\displaystyle{ A }[/math] is the wave amplitude (in potential) [math]\displaystyle{ \mathrm{i} k }[/math] is the positive imaginary solution of the Dispersion Relation for a Free Surface (note we are assuming that the time dependence is of the form [math]\displaystyle{ \exp(-\mathrm{i}\omega t) }[/math]) and
We assume that [math]\displaystyle{ A=1 }[/math]. This gives us
This means that (using the far field behaviour of the potential [math]\displaystyle{ \phi }[/math])
For the present case the body is present only on the surface and we therefore have
Therefore
and using a wave incident from the right we obtain
Note that an expression for the integral in the denominator can be found in Eigenfunction Matching for a Semi-Infinite Dock
Matlab Code
A program to calculate the solution in elastic modes can be found here
Additional code
This program requires