Method of Characteristics for Linear Equations
| Nonlinear PDE's Course | |
|---|---|
| Current Topic | Method of Characteristics for Linear Equations |
| Next Topic | Traffic Waves |
| Previous Topic | |
We present here a brief account of the method of characteristic for linear waves.
Introduction
The method of characteristics is an important method for hyperbolic PDE's which applies to both linear and nonlinear equations.
We begin with the simplest wave equation
subject to the initial conditions
We consider the solution along the curve [math]\displaystyle{ (x,t) = (X(t),t) }[/math]. We then have
Therefore along the curve [math]\displaystyle{ \frac{\mathrm{d} X}{\mathrm{d}t} = 1 }[/math] [math]\displaystyle{ u(x,t) }[/math] must be a constant. These are nothing but the straight lines [math]\displaystyle{ x = t+c }[/math] This means that we have
Therefore the solution is [math]\displaystyle{ u(x,t) = f(x-t)\, }[/math].
General Form
If we consider the equation
then we can apply the method of characteristics. We consider the solution along the curve [math]\displaystyle{ (x,t) = (X(t),t) }[/math]. We then have
[math]\displaystyle{ \frac{\mathrm{d} }{\mathrm{d} t} u(X(t),t) = \partial_t u + \frac{\mathrm{d} X}{\mathrm{d}t}\partial_x u = \partial_x u \left(\frac{\mathrm{d} X}{\mathrm{d}t} - a(x,t) \right). }[/math]
This gives us the following o.d.e. for the characteristic curves (along which the solution is a constant)
[math]\displaystyle{ \frac{\mathrm{d} X}{\mathrm{d} t} = a(x,t) . }[/math]
Example 1
Consider the equation
subject to the initial conditions
We consider the solution along the curve [math]\displaystyle{ (x,t) = (X(t),t) }[/math]. We then have
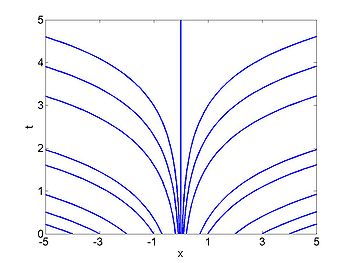
Therefore along the curve [math]\displaystyle{ \frac{\mathrm{d} X}{\mathrm{d}t} = x }[/math] [math]\displaystyle{ u(x,t) }[/math] must be a constant. These are the curves [math]\displaystyle{ x = ce^t }[/math] This means that we have
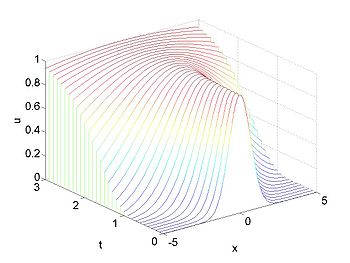
Therefore the solution is given [math]\displaystyle{ u(x,t) = f(xe^{-t})\, }[/math].
Example 2
Consider the equation
subject to the initial conditions
We consider the solution along the curve [math]\displaystyle{ (x,t) = (X(t),t) }[/math]. We then have
Therefore along the curve [math]\displaystyle{ \frac{\mathrm{d} X}{\mathrm{d}t} = t }[/math] [math]\displaystyle{ u(x,t) }[/math] must be a constant. These are the curves [math]\displaystyle{ x = t^2/2+c }[/math] This means that we have
Therefore the solution is given [math]\displaystyle{ u(x,t) = f(x - t^2/2)\, }[/math].
Non-homogeneous Example
We can also use the method of characteristics in the non-homogeneous case. We show this through an example Consider the equation
subject to the initial conditions
We consider the solution along the curve [math]\displaystyle{ (x,t) = (X(t),t) }[/math]. We then have
Therefore along the curve [math]\displaystyle{ \frac{\mathrm{d} X}{\mathrm{d}t} = t }[/math] which are the curves [math]\displaystyle{ x = t^2/2+c }[/math]
[math]\displaystyle{ \frac{\mathrm{d}}{\mathrm{d}t}u(x,t) = xt = t^3/2 + c t }[/math]
Therefore
[math]\displaystyle{ u(t^2/2+c,t) = t^4/8 + c t^2/2 + c_2\, }[/math]
Now
Therefore the solution is given [math]\displaystyle{ u(x,t) = t^4/8 + (x -t^2/2) t^2/2 + f(x-t^2/2)\, }[/math] or [math]\displaystyle{ u(x,t) = -t^4/8 + x t^2/2 + f(x-t^2/2)\, }[/math]
Lecture Videos
Part 1
Part 2
Part 3