Numerical Solution of the KdV

Nonlinear PDE's Course
Current Topic	Numerical Solution of the KdV
Next Topic	Conservation Laws for the KdV
Previous Topic	Introduction to KdV

Introduction

We present here a method to solve the KdV equation numerically. There are many different methods to solve the KdV and we use here a spectral method which has been found to work well. Spectral methods work by using the Fourier transform (or some varient of it) to calculate the derivative.

Fourier Transform

Recall that the Fourier transform is given by

[math]\displaystyle{ \mathcal{F}\left[ f(x)\right] =\hat{f}\left( k\right) =\int_{-\infty }^{\infty }f\left( x\right) \mathrm{e}^{-\mathrm{i}kx}\mathrm{d}x }[/math]

and the inverse Fourier transform is given by

[math]\displaystyle{ f\left( x\right) =\mathcal{F}^{-1}\left[ \hat{f}\left( k\right) \right] = \frac{1}{2\pi }\int_{-\infty }^{\infty }\hat{f}\left( k\right) \mathrm{e}^{\mathrm{i}kx}\mathrm{d}k }[/math]

(note that there are other ways of writing this transform). The most important property of the Fourier transform is that

[math]\displaystyle{ \begin{matrix} \int_{-\infty }^{\infty }\left( \partial _{x}f\left( x\right) \right) \mathrm{e}^{-\mathrm{i}kx}\mathrm{d}x &=&-\int_{-\infty }^{\infty }f\left( x\right) \left( \partial_{x}\mathrm{e}^{-\mathrm{i}kx}\right) \mathrm{d}x \\ &=&ik\int_{-\infty }^{\infty }f\left( x\right) \mathrm{e}^{-\mathrm{i}kx}\mathrm{d}x \end{matrix} }[/math]

where we have assumed that the function [math]\displaystyle{ f\left( x\right) }[/math] vanishes at [math]\displaystyle{ \pm \infty . }[/math] This means that the Fourier transform converts differentiation to multiplication by [math]\displaystyle{ i k }[/math].

Solution for the Linearized KdV

We begin with a simple example. Suppose we want to solve the linearized KdV equation

[math]\displaystyle{ \partial _{t}u+\partial _{x}^{3}u=0,\ \ -\infty \lt x \lt \infty }[/math]

subject to solve initial conditions

[math]\displaystyle{ u\left( x,0\right) =f\left( x\right) }[/math]

We can solve this equation by taking the Fourier transform. and obtain

[math]\displaystyle{ \partial _{t}\hat{u}-ik^{3}\hat{u}=0 }[/math]

So that

[math]\displaystyle{ \hat{u}\left( k,t\right) =\hat{f}\left( k\right) \mathrm{e}^{\mathrm{i}k^{3}t} }[/math]

Therefore

[math]\displaystyle{ u\left( x,t\right) = \frac{1}{2\pi} \int_{-\infty}^{\infty }\hat{f}\left( k\right) \mathrm{e}^{\mathrm{i}k^{3}t}\mathrm{e}^{\mathrm{i}kx}\mathrm{d}k }[/math]

Numerical Implementation Using the FFT

The Fast Fourier Transform (FFT) is a method to calculate the fourier transform efficiently for discrete sets of points. These points need to be evenly spaced in the [math]\displaystyle{ x }[/math] plane and are given by

[math]\displaystyle{ x_{n}=x_{0}+n\Delta x,\ \ 0\leq n\leq N-1 }[/math]

(note they can start at any [math]\displaystyle{ x }[/math] value). For the FFT to be as efficient as possible [math]\displaystyle{ N }[/math] should be a power of [math]\displaystyle{ 2. }[/math] Corresponding to the discrete set of points in the [math]\displaystyle{ x }[/math] domain is a discrete set of points in the [math]\displaystyle{ k }[/math] plane given by

[math]\displaystyle{ k_{n}=\left\{ \begin{matrix} n\Delta k,\ \ 0\leq n\leq \frac{N}{2} \\ \left( n-N\right) \Delta k,\ \ \frac{N}{2}+1\leq n\leq N-1 \end{matrix} \right. }[/math]

where [math]\displaystyle{ \Delta k=2\pi /(N\Delta x). }[/math] Note that this numbering seems slighly odd and is due to aliasing. We are not that interested in the frequency domain solution but we need to make sure that we select the correct values of [math]\displaystyle{ k }[/math] for our numerical code.

Numerical Code for the Linear KdV

Here is the code to solve the linear KdV using MATLAB

N = 1024;

t=0.1;

x = linspace(-10,10,N);

delta_x = x(2) - x(1);

delta_k = 2*pi/(N*delta_x);

k = [0:delta_k:N/2*delta_k,-(N/2-1)*delta_k:delta_k:-delta_k];

f = exp(-x.^2);

f_hat = fft(f);

u = real(ifft(f_hat.*exp(i*k.^3*t)));

Numerical Solution of the KdV

It turns out that a method to solve the KdV equation can be derived using spectral methods. We begin with the KdV equation written as

[math]\displaystyle{ \partial _{t}u+3\partial _{x}\left( u\right) ^{2}+\partial _{x}^{3}u=0. }[/math]

The Fourier transform of the KdV is therefore

[math]\displaystyle{ \partial _{t}\hat{u}+3ik\widehat{\left( u^{2}\right)} -ik^{3}\hat{u}=0 }[/math]

We solve this equation by a split step method. We write the equation as

[math]\displaystyle{ \partial _{t}\hat{u}=-3ik\widehat{\left( u^{2}\right)} +ik^{3}\hat{u} }[/math]

We can solve

[math]\displaystyle{ \partial _{t}\hat{u}=ik^{3}\hat{u} }[/math]

exactly while the equation

[math]\displaystyle{ \partial _{t}\hat{u}=-3ik\widehat{\left( u^{2}\right)} }[/math]

needs to be solved by time stepping. The idea of the split step method is to solve alternatively each of these equations when stepping from [math]\displaystyle{ t }[/math] to [math]\displaystyle{ t+\Delta t. }[/math] Therefore we solve

[math]\displaystyle{ \begin{matrix} \hat{u}_{1}\left( k,t+\Delta t\right) &=&\hat{u}\left( k,t\right) \mathrm{e}^{\mathrm{i}k^{3}\Delta t} \\ \hat{u}\left( k,t+\Delta t\right) &=&\hat{u}_{1}\left( k,t+\Delta t\right) -3ik \Delta t\widehat{\left( u_{1}^{2}\right)} \end{matrix} }[/math]

Note that we are using Euler's method to time step and that the solution could be improved by using a better method, such as the Runge-Kutta 4 method.

The only slighly tricky thing is that we have both [math]\displaystyle{ u }[/math] and [math]\displaystyle{ \hat{u} }[/math] in the equation, but we can simply use the Fourier transform to connect these. The equation then becomes

[math]\displaystyle{ \begin{matrix} \hat{u}_{1}\left( k,t+\Delta t\right) &=&\hat{u}\left( k,t\right) \mathrm{e}^{\mathrm{i}k^{3}\Delta t} \\ \hat{u}\left( k,t+\Delta t\right) &=&\hat{u}_{1}\left( k,t+\Delta t\right) - 3ik\Delta t\left( \mathcal{F}\left( \left( \mathcal{F}^{-1}\left[ \hat{u}_{1}\left( k,t+\Delta t\right)\right] \right) ^{2}\right) \right) \end{matrix} }[/math]

Numerical Code to solve the KdV by the split step method

Here is some code to solve the KdV using MATLAB

N = 256;

x = linspace(-10,10,N);

delta_x = x(2) - x(1);

delta_k = 2*pi/(N*delta_x);

k = [0:delta_k:N/2*delta_k,-(N/2-1)*delta_k:delta_k:-delta_k];

c=16;

u = 1/2*c*(sech(sqrt(c)/2*(x+8))).^2;

delta_t = 0.4/N^2;

tmax = 0.1; nmax = round(tmax/delta_t);

U = fft(u);

for n = 1:nmax

% first we solve the linear part

U = U.*exp(1i*k.^3*delta_t);

%then we solve the non linear part

U = U - delta_t*(3i*k.*fft(real(ifft(U)).^2));

end

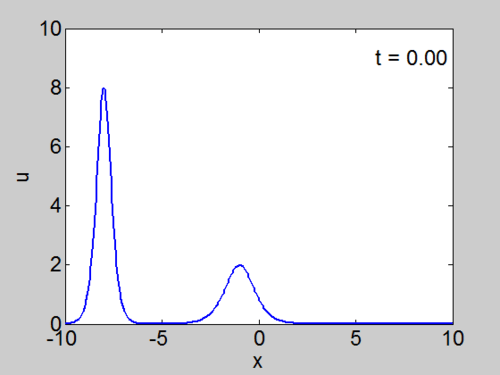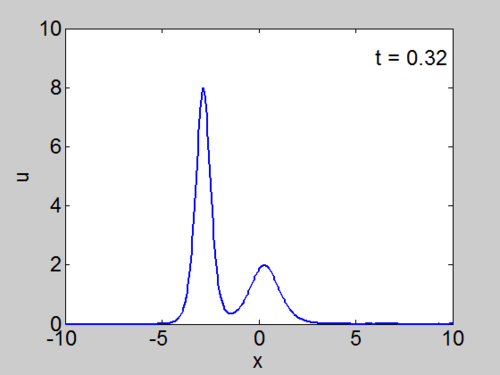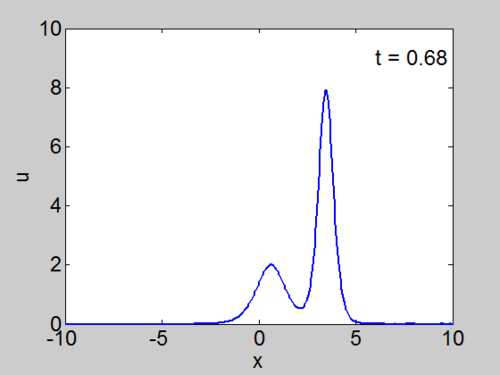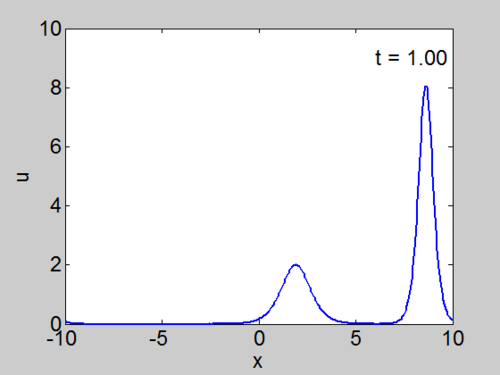
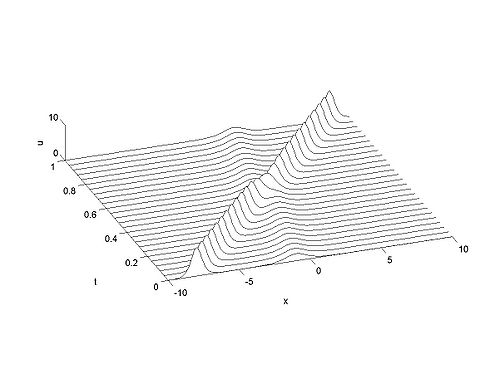
Example Calculations

We cosider the evolution of the KdV with two solitons as initial condition as given below.

[math]\displaystyle{ u(x,0) = 8\,\mathrm{sech}^{2}\left(2(x+8)\right) + \, 2 \mathrm{sech}^{2}\left(\left( x +1\right) \right) }[/math]

Animation	Three-dimensional plot.
Evolution of [math]\displaystyle{ u(x,t) }[/math] for two solitons.	Evolution of [math]\displaystyle{ u(x,t) }[/math] for two solitons. Note the phase shift which occurs in the soliton interaction.