Wave Forecasting
Our understanding of ocean waves, their spectra, their generation by the wind, and their interactions are now sufficiently well understood that the wave spectrum can be forecast using winds calculated from numerical weather models. If we observe some small ocean area, or some area just offshore, we can see waves generated by the local wind, the wind sea, plus waves that were generated in other areas at other times and that have propagated into the area we are observing, the swell. Forecasts of local wave conditions must include both sea and swell, hence wave forecasting is not a local problem. We saw, for example, that waves off California can be generated by storms more than 10,000km away.
Various techniques have been used to forecast waves. The earliest attempts were based on empirical relationships between wave-height and wave-length and wind speed, duration, and fetch. The development of the wave spectrum allowed evolution of individual wave components with frequency [math]\displaystyle{ f }[/math] traveling in direction [math]\displaystyle{ \theta }[/math] of the directional wave spectrum [math]\displaystyle{ \psi\mbox{ }( f,\mbox{ } \theta) }[/math] using
where [math]\displaystyle{ \psi_0 = \psi_0\mbox{ }( f,\mbox{ } \theta,\mbox{ } x,\mbox{ } t ) }[/math] varies in space [math]\displaystyle{ (x) }[/math] and time [math]\displaystyle{ t,\mbox{ } S_i }[/math] is input from the wind given by the Phillips 1957 and Miles 1957 mechanisms, [math]\displaystyle{ S_{nl} }[/math] is the transfer among wave components due to nonlinear interactions (Figure 1), and [math]\displaystyle{ S_d }[/math] is dissipation.
The third-generation wave-forecasting models now used by meteorological agencies throughout the world are based on integrations of the above equation using many individual wave components (The SWAMP Group 1985; The WAMDI Group, 1988; Komen et al., 1994). The forecasts follow individual components of the wave spectrum in space and time, allowing each component to grow or decay depending on local winds, and allowing wave components to interact according to Hasselmann's theory. Typically the sea is represented by 300 components: 25 wavelengths going in 12 directions (30°). Each component is allowed to propagate from grid point to grid point, growing with the wind or decaying in time, all the while interacting with other waves in the spectrum. To reduce computing time, the models use a nested grid of points: the grid has a high density of points in storms and near coasts and a low density in other regions. Typically, grid points in the open ocean are 3° apart.
Some recent experimental models take the wave-forecasting process one step further by assimilating altimeter and scatterometer observations of wind speed and wave-height into the model. Forecasts of waves using assimilated satellite data are available from the European Centre for Medium-Range Weather Forecasts. Details of the third-generation models produced by the Wave Analysis Group (WAM) are described in the book by Komen et al. 1996.
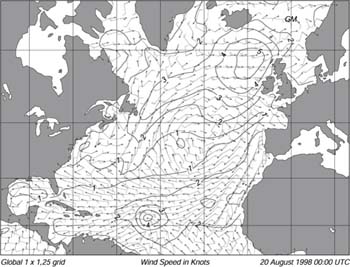
NOAA's Ocean Modelling Branch at the National Centers for Environmental Predictions also produces regional and global forecasts of waves. The Branch use a third-generation model based on the Cycle-4 WAM model. It accommodates ever-changing ice edge, and it assimilates buoy and satellite altimeter wave data. The model calculates directional frequency spectra in 12 directions and 25 frequencies at 3-hour intervals up to 72 hours in advance. The lowest frequency is 0.04177 Hz and higher frequencies are spaced logarithmically at increments of 0.1 times the lowest frequency. Wave spectral data are available on a 2.5° ?2.5° grid for deep-water points between 67.5°S and 77.5°N. The model is driven using 10m winds calculated from the lowest winds from the Centers weather model adjusted to a height of 10m by using a logarithmic profile (8.19). The Branch is testing an improved forecast with 1° ?1.25° resolution (Figure 1).
Figure 1 Output of a third-generation wave forecast model produced by NOAA Ocean Modeling Branch for 20 August 1998. Contours are significant wave-height in meters, arrows give direction of waves at the peak of the wave spectrum, and barbs give wind speed in m/s and direction. From NOAA Ocean Modeling Branch.
Acknowledgement
The material in this page has come from Introduction to Physical Oceanography by Robert Stewart.