Waves and the Concept of a Wave Spectrum

Introduction

If we look out to sea, we notice that waves on the sea surface are not simple sinusoids. The surface appears to be composed of random waves of various lengths and periods. How can we describe this surface? The simple answer is, Not very easily. We can however, with some simplifications, come close to describing the surface. The simplifications lead to the concept of the spectrum of ocean waves. The spectrum gives the distribution of wave energy among different wave frequencies of wave-lengths on the sea surface.

The concept of a spectrum is based on work by Joseph Fourier (1768 - 1830), who showed that almost any function [math]\displaystyle{ \zeta(t) }[/math] (or [math]\displaystyle{ \zeta(x) }[/math] if you like), can be represented over the interval [math]\displaystyle{ -T/2 \lt t \lt T/2 }[/math] as the sum of an infinite series of sine and cosine functions with harmonic wave frequencies:

[math]\displaystyle{ \zeta(t) = \frac{a_0}{2}+\sum_{n=1}^\infty (a_n\cos(2{\pi}nft)+b_n\sin(2{\pi}nft)) \,\! }[/math]

where

[math]\displaystyle{ a_n=\frac{2}{T}\int_{-T/2}^{T/2}\zeta(t)\cos(2{\pi}nft)\mathrm{d}t,\qquad (n=0,1,2,...) }[/math] [math]\displaystyle{ b_n=\frac{2}{T}\int_{-T/2}^{T/2}\zeta(t)\sin(2{\pi}nft)\mathrm{d}t,\qquad(n=0,1,2,...) }[/math]

[math]\displaystyle{ f = 1/T }[/math] is the fundamental frequency, and [math]\displaystyle{ nf }[/math] are harmonics of the fundamental frequency. This form of [math]\displaystyle{ \zeta(t) }[/math] is called a Fourier series. Notice that [math]\displaystyle{ a_0 }[/math] is the mean value of [math]\displaystyle{ \zeta(t) }[/math] over the interval.

These equations can be simplified using

[math]\displaystyle{ \exp(2{\pi}inft)=\cos(2{\pi}nft)+i\sin(2{\pi}nft)\, }[/math]

where [math]\displaystyle{ i = \sqrt{-1} }[/math]. The equations for the Fourier Series then become:

[math]\displaystyle{ \zeta(t)=\sum_{n=-\infty}^\infty Z_n\,\exp^{i2{\pi}nft} }[/math]

where

[math]\displaystyle{ Z_n=\frac{1}{T}\int_{-T/2}^{T/2}\zeta(t)\,\exp^{-i2{\pi}nft}\,\mathrm{d}t, \qquad(n=0,1,2,...) }[/math]

[math]\displaystyle{ Z_n }[/math] is called the complex Fourier series of [math]\displaystyle{ \zeta(t) }[/math]. This form is preferable and is the basis of algorithms like the Fast Fourier Transform

The spectrum [math]\displaystyle{ S(f) }[/math] of [math]\displaystyle{ \zeta(t) }[/math] is:

[math]\displaystyle{ S(nf)=Z_n Z_n^* }[/math]

where [math]\displaystyle{ Z_n^* }[/math] is the complex conjugate of [math]\displaystyle{ Z_n }[/math]. We will use these forms for the Fourier series and spectra when we describe the computation of ocean wave spectra.

We can expand the idea of a Fourier series to include series that represent surfaces [math]\displaystyle{ \zeta(x,y) }[/math] using similar techniques. Thus, any surface can be represented as an infinite series of sine and cosine functions oriented in all possible directions.

Now, let's apply these ideas to the sea surface. Suppose for a moment that the sea surface were frozen in time. Using the Fourier expansion, the frozen surface can be represented as an infinite series of sine and cosine functions of different wave numbers oriented in all possible directions. If we unfreeze the surface and let it evolve in time, we can represent the sea surface as an infinite series of sine and cosine functions of different wave-lengths moving in all directions. Because wave-lengths and wave frequencies are related through the dispersion relation, we can also represent the sea surface as an infinite sum of sine and cosine functions of different frequencies moving in all directions.

Note in our discussion of Fourier series that we assume the coefficients [math]\displaystyle{ (a_n,\mbox{ }b_n,\mbox{ } Z_n) }[/math] are constant. For times of perhaps an hour, and distances of perhaps tens of kilometers, the waves on the sea surface are sufficiently fixed that the assumption is true. Furthermore, non-linear interactions among waves are very weak. Therefore, we can represent a local sea surface by a linear super-position of real, sine waves having many different wave-lengths or frequencies and different phases traveling in many different directions. The Fourier series in not just a convenient mathematical expression, it states that the sea surface is really, truly composed of sine waves, each one propagating according to the equations in Linear Theory of Ocean Surface Waves.

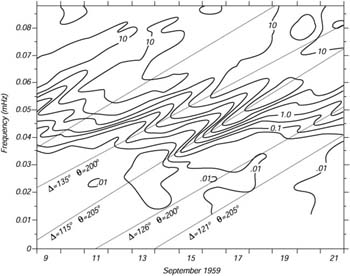
The concept of the sea surface being composed of independent waves can be carried further. Suppose I throw a rock into a calm ocean, and it makes a big splash. According to Fourier, the splash can be represented as a superposition of cosine waves all of nearly zero phase so the waves add up to a big splash at the origin. Furthermore, each individual Fourier wave then begins to travel away from the splash. The longest waves travel fastest, and eventually, far from the splash, the sea consists of a dispersed train of waves with the longest waves further from the splash and the shortest waves closest. This is exactly what we see in Figure 1. The storm makes the splash, and the waves disperse as seen in the figure.

Figure 1 Contours of wave energy on a frequency-time plot calculated from spectra of waves measured by pressure gauges offshore of southern California. The ridges of high wave energy show the arrival of dispersed wave trains from distant storms. The slope of the ridge is inversely proportional to distance to the storm. D is distance in degrees, [math]\displaystyle{ \theta }[/math] is direction of arrival of waves at California. From Munk et al. 1963. (this figure is discussed in detail in Linear Theory of Ocean Surface Waves).

Sampling the Sea Surface

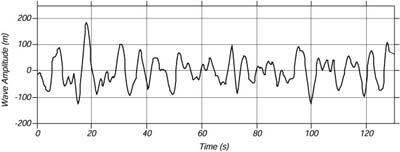
Calculating the Fourier series that represents the sea surface is perhaps impossible. It requires that we measure the height of the sea surface [math]\displaystyle{ \zeta(x,\,y,\,t) }[/math] everywhere in an area perhaps ten kilometers on a side for perhaps an hour. So, let's simplify. Suppose we install a wave staff somewhere in the ocean and record the height of the sea surface as a function of time [math]\displaystyle{ \zeta(t) }[/math]. We would obtain a record like that in Figure 2. All waves on the sea surface will be measured, but we will know nothing about the direction of the waves. This is a much more practical measurement, and it will give the frequency spectrum of the waves on the sea surface.

Figure 2. A short record of wave amplitude measured by a wave buoy in the North Atlantic.

Working with a trace of wave-height on say a piece of paper is difficult, so let's digitize the output of the wave staff to obtain

[math]\displaystyle{ \begin{matrix}\zeta_j\equiv\zeta(t_j), & \qquad & t_j \equiv j\triangle \\ \ & \qquad & j=0,1,2,...,N-1 \end{matrix} }[/math]

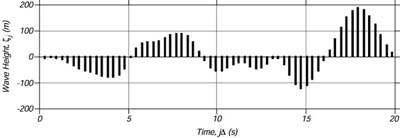
where [math]\displaystyle{ \Delta }[/math] is the time interval between the samples, and [math]\displaystyle{ N }[/math] is the total number of samples. The length [math]\displaystyle{ T }[/math] of the record is [math]\displaystyle{ T = N\Delta }[/math]. Figure 3 shows the first 20 seconds of wave-height from Figure 2 digitized at intervals of [math]\displaystyle{ \Delta }[/math] = 0.32 s.

Figure 3 The first 20 seconds of digitized data from Figure 2. [math]\displaystyle{ \Delta }[/math] = 0.32s.

Notice that [math]\displaystyle{ \zeta_j }[/math] is not the same as [math]\displaystyle{ \zeta(t) }[/math].We have absolutely no information about the height of the sea surface between samples. Thus we have converted from an infinite set of numbers which describes [math]\displaystyle{ \zeta(t) }[/math] to a finite set of numbers which describe [math]\displaystyle{ \zeta_j }[/math]. By converting from a continuous function to a digitized function, we have given up an infinite amount of information about the surface.

The sampling interval [math]\displaystyle{ \Delta }[/math] defines a Nyquist critical frequency (Press et al. 1992: 494) [math]\displaystyle{ N_y = 1/(2\Delta) }[/math].

The Nyquist critical frequency is important for two related, but distinct, reasons. One is good news, the other is bad news. First the good news. It is the remarkable fact known as the sampling theorem: If a continuous function [math]\displaystyle{ z(t) }[/math] , sampled at an interval [math]\displaystyle{ \Delta }[/math], happens to be bandwidth limited to frequencies smaller in magnitude than [math]\displaystyle{ N_y }[/math], i.e. if [math]\displaystyle{ S(f) = 0 }[/math] for all [math]\displaystyle{ |f| \gt N_y }[/math], then the function [math]\displaystyle{ z(t) }[/math] is completely determined by its samples [math]\displaystyle{ z_j }[/math]. This is a remarkable theorem for many reasons, among them that it shows that the "information content" of a bandwidth limited function is, in some sense, infinitely smaller than that of a general continuous function.

Now the bad news. The bad news concerns the effect of sampling a continuous function that is not bandwidth limited to less than the Nyquist critical frequency. In that case, it turns out that all of the power spectral density that lies outside the frequency range -Ny < nf < Ny is spuriously moved into that range. This phenomenon is called aliasing. Any frequency component outside of the range (-Ny, Ny ) is aliased (falsely translated) into that range by the very act of discrete sampling... There is little that you can do to remove aliased power once you have discretely sampled a signal. The way to overcome aliasing is to (i) know the natural bandwidth limit of the signal - or else enforce a known limit by analog filtering of the continuous signal, and then (ii) sample at a rate sufficiently rapid to give at least two points per cycle of the highest frequency present.

Figure 4 illustrates the aliasing problem. Notice how a high frequency signal is aliased into a lower frequency if the higher frequency is above the critical frequency. Fortunately, we can can easily avoid the problem: (i) use instruments that do not respond to very short, high frequency waves if we are interested in the bigger waves; and (ii) chose [math]\displaystyle{ \Delta }[/math] small enough that we lose little useful information. In the example shown in Figure 3, there are no waves in the signal to be digitized with frequencies higher than [math]\displaystyle{ N_y }[/math] = 1.5625 Hz.

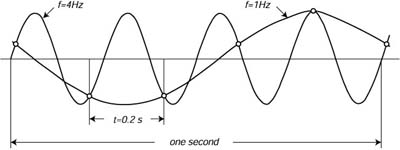
Figure 4 Sampling a 4 Hz sine wave (heavy Line) every 0.2 s aliases the frequency to 1 Hz (light line) The critical frequency is [math]\displaystyle{ 1/(2 \times 0.2 }[/math] s) = 2.5 Hz, which is less than 4 Hz.

Let's summarize. Digitized signals from a wave staff cannot be used to study waves with frequencies above the Nyquist critical frequency. Nor can the signal be used to study waves with frequencies less than the fundamental frequency determined by the duration T of the wave record. The digitized wave record contains information about waves in the frequency range:

[math]\displaystyle{ \frac{1}{T}\lt f\lt \frac{1}{2\triangle} }[/math]

where [math]\displaystyle{ T = N\Delta }[/math] is the length of the time series, and [math]\displaystyle{ f }[/math] is the frequency in Hertz.

Calculating The Wave Spectrum

The discrete Fourier transform [math]\displaystyle{ Z_n }[/math] of a wave record [math]\displaystyle{ \zeta_j }[/math] is:

[math]\displaystyle{ Z_n=\frac{1}{N}\sum_{j=0}^{N-1}\,\zeta_j\,\exp[-i2{\pi}jn/N] }[/math] [math]\displaystyle{ \zeta_j=\sum_{n=0}^{N-1}\,Z_j\,\exp[i2{\pi}jn/N]\, }[/math]

for [math]\displaystyle{ j \,=\, 0,\, 1, \dots,\, N\, -\, 1; \,n\, = \,0, \,1, \dots, \,N \,- \,1 }[/math]. These equations can be summed very quickly using the Fast Fourier Transform, especially if [math]\displaystyle{ N }[/math] is a power of 2 (Cooley, Lewis, and Welch 1970; Press et al. 1992: 542).

The simple spectrum [math]\displaystyle{ S_n }[/math] of [math]\displaystyle{ \zeta_j }[/math], which is called the periodogram, is:

[math]\displaystyle{ S_n=\frac{1}{N^2}[|Z_n| ^2+|Z_{N-n}|^2];\qquad n=1,2,...,(N/2-1) }[/math] [math]\displaystyle{ S_0=\frac{1}{N^2}|Z_0|^2 }[/math] [math]\displaystyle{ S_{N/2}=\frac{1}{N^2}|Z_{N/2}|^2 }[/math]

where [math]\displaystyle{ S_N }[/math] is normalized such that:

[math]\displaystyle{ \sum_{j=0}^{N-1}\,|\zeta_j|^2=\sum_{n=0}^{N/1}S_n }[/math]

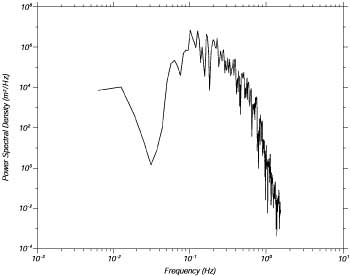
thus the variance of [math]\displaystyle{ \zeta_j }[/math] is the sum of the [math]\displaystyle{ (N/2\, + \,1) }[/math] terms in the periodogram. Note, the terms of [math]\displaystyle{ S_n }[/math] above the frequency [math]\displaystyle{ (N/2) }[/math] are symmetric about that frequency. Figure 5 shows the periodogram of the time series shown in Figure 2.

Figure 5 The periodogram calculated from the first 164s of data from Figure 2. The Nyquist frequency is 1.5625Hz.

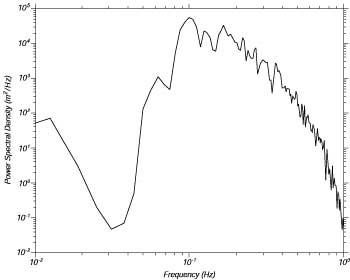
The periodogram is a very noisy function. The variance of each point is equal to the expected value at the point. By averaging together 10-30 periodograms we can reduce the uncertainty in the value at each frequency. The averaged periodogram is called the spectrum of the wave-height (Figure 6). It gives the distribution of the variance of sea-surface (the height the sea surface would be if there were no waves) height at the wave staff as a function of frequency. Because wave energy is proportional to the variance the spectrum is called the energy spectrum or the wave-height spectrum. Typically three hours of wave staff data are used to compute a spectrum of wave-height.

Figure 6 The spectrum of waves calculated from 11 minutes of data shown in Figure 2 by averaging four periodograms to reduce uncertainty in the spectral values. Spectral values below 0.04Hz are in error due to noise.

Summary

We can summarize the calculation of a spectrum into the following steps:

1. Digitize a segment of wave-height data to obtain useful limits according to out equations. For example, use 1024 samples from 8.53 minutes of data sampled at the rate of 2 samples/second.
2. Calculate the digital, fast Fourier transform [math]\displaystyle{ Z_n }[/math] of the time series.
3. Calculate the periodogram [math]\displaystyle{ S_n }[/math] from the sum of the squares of the real and imaginary parts of the Fourier transform.
4. Repeat to produce M = 20 periodograms.
5. Average the 20 periodograms to produce an averaged spectrum [math]\displaystyle{ S_M }[/math].
6. [math]\displaystyle{ S_M }[/math] has values that are [math]\displaystyle{ \chi^2 }[/math] distributed with [math]\displaystyle{ 2M }[/math] degrees of freedom.

This outline of the calculation of a spectrum ignores many details. For more complete information see, for example, Percival and Walden 1993, Press et al. 1992, Oppenheim and Schafer 1975, or other texts on digital signal processing.

Acknowledgement

The material in this page has come from Introduction to Physical Oceanography by Robert Stewart.