Difference between revisions of "Method of Characteristics for Linear Equations"
(→Part 1) |
|||
| (20 intermediate revisions by 3 users not shown) | |||
| Line 4: | Line 4: | ||
| previous chapter = | | previous chapter = | ||
}} | }} | ||
| + | |||
| + | {{complete pages}} | ||
We present here a brief account of the method of characteristic for linear waves. | We present here a brief account of the method of characteristic for linear waves. | ||
| Line 15: | Line 17: | ||
<center> | <center> | ||
<math> | <math> | ||
| − | \partial_t u + \partial_x u = 0,\,\,-\infty<x<\infty,\,\,t>0, | + | \partial_t u + \partial_x u = 0,\,\,-\infty < x < \infty,\,\,t>0, |
</math></center> | </math></center> | ||
subject to the initial conditions | subject to the initial conditions | ||
| Line 26: | Line 28: | ||
<center> | <center> | ||
<math> | <math> | ||
| − | \frac{d | + | \frac{\mathrm{d} }{\mathrm{d} t} u(X(t),t) = \partial_t u + \frac{\mathrm{d} X}{\mathrm{d}t}\partial_x u = \partial_x u \left(\frac{\mathrm{d} X}{\mathrm{d}t} - 1 \right) |
</math></center> | </math></center> | ||
| − | Therefore along the curve <math>\frac{d X}{ | + | Therefore along the curve <math>\frac{\mathrm{d} X}{\mathrm{d}t} = 1</math> <math>u(x,t)</math> must be a constant. |
These are nothing but the straight lines <math>x = t+c</math> | These are nothing but the straight lines <math>x = t+c</math> | ||
This means that we have | This means that we have | ||
<center> | <center> | ||
<math> | <math> | ||
| − | u(x,t) = u(-t+c,t) = u(c,0) = f(c) = f(x+t) | + | u(x,t) = u(t+c,t) = u(c,0) = f(c) = f(x-t)\, |
| + | </math></center> | ||
| + | Therefore the solution is <math>u(x,t) = f(x-t)\,</math>. | ||
| + | |||
| + | == General Form == | ||
| + | |||
| + | If we consider the equation | ||
| + | <center> | ||
| + | <math> | ||
| + | \partial_t u + a(x,t)\partial_x u = 0,\,\,-\infty < x < \infty,\,\,t>0, | ||
| + | </math></center> | ||
| + | then we can apply the method of characteristics. | ||
| + | We consider the solution along the curve <math>(x,t) = (X(t),t)</math>. We then have | ||
| + | <center> | ||
| + | <math> | ||
| + | \frac{\mathrm{d} }{\mathrm{d} t} u(X(t),t) = \partial_t u + \frac{\mathrm{d} X}{\mathrm{d}t}\partial_x u = \partial_x u \left(\frac{\mathrm{d} X}{\mathrm{d}t} - a(x,t) \right). | ||
| + | </math> | ||
| + | </center> | ||
| + | This gives us the following o.d.e. for the characteristic curves (along which the solution is a constant) | ||
| + | <center> | ||
| + | <math> | ||
| + | \frac{\mathrm{d} X}{\mathrm{d} t} = a(x,t) . | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | == Example 1 == | ||
| + | |||
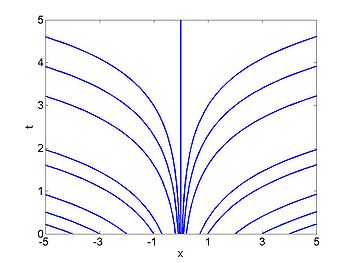
| + | [[Image:Characteristic_linear1.jpg|thumb|right|350px|Characteristic for Example 1]] | ||
| + | Consider the equation | ||
| + | <center> | ||
| + | <math> | ||
| + | \partial_t u + x \partial_x u = 0,\,\,-\infty < x < \infty,\,\,t>0, | ||
| + | </math></center> | ||
| + | subject to the initial conditions | ||
| + | <center> | ||
| + | <math> | ||
| + | \left. u \right|_{t=0} = f(x) | ||
| + | </math></center> | ||
| + | |||
| + | We consider the solution along the curve <math>(x,t) = (X(t),t)</math>. We then have | ||
| + | <center> | ||
| + | <math> | ||
| + | \frac{\mathrm{d} }{\mathrm{d} t} u(X(t),t) = \partial_t u + \frac{\mathrm{d}X}{\mathrm{d}t}\partial_x u = \partial_x u \left(\frac{\mathrm{d} X}{\mathrm{d}t} - x \right) | ||
| + | </math></center> | ||
| + | |||
| + | Therefore along the curve <math>\frac{\mathrm{d} X}{\mathrm{d}t} = x</math> <math>u(x,t)</math> must be a constant. | ||
| + | These are the curves <math>x = ce^t</math> | ||
| + | This means that we have | ||
| + | <center> | ||
| + | <math> | ||
| + | u(x,t) = u(ce^t,t) = u(c,0) = f(c) = f(xe^{-t})\, | ||
| + | </math></center> | ||
| + | Therefore the solution is given <math>u(x,t) = f(xe^{-t})\,</math>. | ||
| + | |||
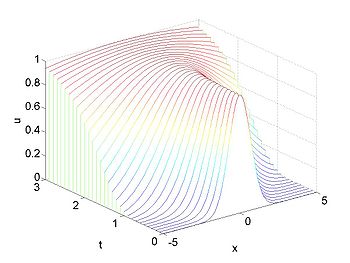
| + | [[Image:Waterfall_linear1.jpg|thumb|right|350px|Solution for Example 1 with <math>f(x) = e^{-x^2}</math>]] | ||
| + | |||
| + | == Example 2 == | ||
| + | |||
| + | Consider the equation | ||
| + | <center> | ||
| + | <math> | ||
| + | \partial_t u + t \partial_x u = 0,\,\,-\infty < x < \infty,\,\,t>0, | ||
| + | </math></center> | ||
| + | subject to the initial conditions | ||
| + | <center> | ||
| + | <math> | ||
| + | \left. u \right|_{t=0} = f(x) | ||
| + | </math></center> | ||
| + | |||
| + | We consider the solution along the curve <math>(x,t) = (X(t),t)</math>. We then have | ||
| + | <center> | ||
| + | <math> | ||
| + | \frac{\mathrm{d} }{\mathrm{d} t} u(X(t),t) = \partial_t u + \frac{\mathrm{d} X}{\mathrm{d}t}\partial_x u = \partial_x u \left(\frac{\mathrm{d} X}{\mathrm{d}t} - t \right) | ||
| + | </math></center> | ||
| + | |||
| + | Therefore along the curve <math>\frac{\mathrm{d} X}{\mathrm{d}t} = t</math> <math>u(x,t)</math> must be a constant. | ||
| + | These are the curves <math>x = t^2/2+c</math> | ||
| + | This means that we have | ||
| + | <center> | ||
| + | <math> | ||
| + | u(x,t) = u(t^2/2 + c,t) = u(c,0) = f(c) = f(x - t^2/2)\, | ||
| + | </math></center> | ||
| + | Therefore the solution is given <math>u(x,t) = f(x - t^2/2)\,</math>. | ||
| + | |||
| + | == Non-homogeneous Example == | ||
| + | |||
| + | We can also use the method of characteristics in the non-homogeneous case. We show this through an example | ||
| + | Consider the equation | ||
| + | <center> | ||
| + | <math> | ||
| + | \partial_t u + t \partial_x u = xt,\,\,-\infty < x < \infty,\,\,t>0, | ||
| + | </math></center> | ||
| + | subject to the initial conditions | ||
| + | <center> | ||
| + | <math> | ||
| + | \left. u \right|_{t=0} = f(x) | ||
| + | </math></center> | ||
| + | |||
| + | We consider the solution along the curve <math>(x,t) = (X(t),t)</math>. We then have | ||
| + | <center> | ||
| + | <math> | ||
| + | \frac{\mathrm{d} u}{\mathrm{d} t} = \partial_t u + \frac{\mathrm{d} X}{\mathrm{d}t}\partial_x u = \partial_x u \left(\frac{\mathrm{d}X}{\mathrm{d}t} - t \right) + xt | ||
| + | </math></center> | ||
| + | |||
| + | Therefore along the curve <math>\frac{\mathrm{d} X}{\mathrm{d}t} = t</math> which are the curves <math>x = t^2/2+c</math> | ||
| + | <center> | ||
| + | <math> | ||
| + | \frac{\mathrm{d}}{\mathrm{d}t}u(x,t) = xt = t^3/2 + c t | ||
| + | </math> | ||
| + | |||
| + | |||
| + | </center> | ||
| + | Therefore | ||
| + | <center> | ||
| + | <math> | ||
| + | u(t^2/2+c,t) = t^4/8 + c t^2/2 + c_2\, | ||
| + | </math> | ||
| + | </center> | ||
| + | Now | ||
| + | <center> | ||
| + | <math> | ||
| + | u(c,0) = c_2 = f(c) | ||
</math></center> | </math></center> | ||
| − | Therefore the solution is given | + | |
| + | Therefore the solution is given <math>u(x,t) = t^4/8 + (x -t^2/2) t^2/2 + f(x-t^2/2)\,</math> or | ||
| + | <math>u(x,t) = -t^4/8 + x t^2/2 + f(x-t^2/2)\,</math> | ||
| + | |||
| + | == Lecture Videos == | ||
| + | |||
| + | === Part 1 === | ||
| + | |||
| + | {{#ev:youtube|zXEvCJyHQSg}} | ||
| + | |||
| + | === Part 2 === | ||
| + | |||
| + | {{#ev:youtube|vRRVU4VrxV0}} | ||
| + | |||
| + | === Part 3 === | ||
| + | |||
| + | {{#ev:youtube|xkGdvFGit_c}} | ||
| + | |||
| + | |||
| + | === Part 4 === | ||
| + | |||
| + | {{#ev:youtube|rW-voMoG0KI}} | ||
Latest revision as of 05:25, 7 August 2020
| Nonlinear PDE's Course | |
|---|---|
| Current Topic | Method of Characteristics for Linear Equations |
| Next Topic | Traffic Waves |
| Previous Topic | |
We present here a brief account of the method of characteristic for linear waves.
Introduction
The method of characteristics is an important method for hyperbolic PDE's which applies to both linear and nonlinear equations.
We begin with the simplest wave equation
subject to the initial conditions
We consider the solution along the curve [math]\displaystyle{ (x,t) = (X(t),t) }[/math]. We then have
Therefore along the curve [math]\displaystyle{ \frac{\mathrm{d} X}{\mathrm{d}t} = 1 }[/math] [math]\displaystyle{ u(x,t) }[/math] must be a constant. These are nothing but the straight lines [math]\displaystyle{ x = t+c }[/math] This means that we have
Therefore the solution is [math]\displaystyle{ u(x,t) = f(x-t)\, }[/math].
General Form
If we consider the equation
then we can apply the method of characteristics. We consider the solution along the curve [math]\displaystyle{ (x,t) = (X(t),t) }[/math]. We then have
[math]\displaystyle{ \frac{\mathrm{d} }{\mathrm{d} t} u(X(t),t) = \partial_t u + \frac{\mathrm{d} X}{\mathrm{d}t}\partial_x u = \partial_x u \left(\frac{\mathrm{d} X}{\mathrm{d}t} - a(x,t) \right). }[/math]
This gives us the following o.d.e. for the characteristic curves (along which the solution is a constant)
[math]\displaystyle{ \frac{\mathrm{d} X}{\mathrm{d} t} = a(x,t) . }[/math]
Example 1
Consider the equation
subject to the initial conditions
We consider the solution along the curve [math]\displaystyle{ (x,t) = (X(t),t) }[/math]. We then have
Therefore along the curve [math]\displaystyle{ \frac{\mathrm{d} X}{\mathrm{d}t} = x }[/math] [math]\displaystyle{ u(x,t) }[/math] must be a constant. These are the curves [math]\displaystyle{ x = ce^t }[/math] This means that we have
Therefore the solution is given [math]\displaystyle{ u(x,t) = f(xe^{-t})\, }[/math].
Example 2
Consider the equation
subject to the initial conditions
We consider the solution along the curve [math]\displaystyle{ (x,t) = (X(t),t) }[/math]. We then have
Therefore along the curve [math]\displaystyle{ \frac{\mathrm{d} X}{\mathrm{d}t} = t }[/math] [math]\displaystyle{ u(x,t) }[/math] must be a constant. These are the curves [math]\displaystyle{ x = t^2/2+c }[/math] This means that we have
Therefore the solution is given [math]\displaystyle{ u(x,t) = f(x - t^2/2)\, }[/math].
Non-homogeneous Example
We can also use the method of characteristics in the non-homogeneous case. We show this through an example Consider the equation
subject to the initial conditions
We consider the solution along the curve [math]\displaystyle{ (x,t) = (X(t),t) }[/math]. We then have
Therefore along the curve [math]\displaystyle{ \frac{\mathrm{d} X}{\mathrm{d}t} = t }[/math] which are the curves [math]\displaystyle{ x = t^2/2+c }[/math]
[math]\displaystyle{ \frac{\mathrm{d}}{\mathrm{d}t}u(x,t) = xt = t^3/2 + c t }[/math]
Therefore
[math]\displaystyle{ u(t^2/2+c,t) = t^4/8 + c t^2/2 + c_2\, }[/math]
Now
Therefore the solution is given [math]\displaystyle{ u(x,t) = t^4/8 + (x -t^2/2) t^2/2 + f(x-t^2/2)\, }[/math] or [math]\displaystyle{ u(x,t) = -t^4/8 + x t^2/2 + f(x-t^2/2)\, }[/math]
Lecture Videos
Part 1
Part 2
Part 3