Difference between revisions of "Numerical Solution of the KdV"
| (20 intermediate revisions by 3 users not shown) | |||
| Line 5: | Line 5: | ||
}} | }} | ||
| − | + | == Introduction == | |
| − | |||
| − | |||
| − | |||
| − | = | ||
We present here a method to solve the KdV equation numerically. There are | We present here a method to solve the KdV equation numerically. There are | ||
many different methods to solve the KdV and we use here a spectral method | many different methods to solve the KdV and we use here a spectral method | ||
| − | which has been found to work well. | + | which has been found to work well. Spectral methods work by using the |
Fourier transform (or some varient of it) to calculate the derivative. | Fourier transform (or some varient of it) to calculate the derivative. | ||
| Line 35: | Line 31: | ||
\mathrm{e}^{-\mathrm{i}kx}\mathrm{d}x &=&-\int_{-\infty }^{\infty }f\left( x\right) | \mathrm{e}^{-\mathrm{i}kx}\mathrm{d}x &=&-\int_{-\infty }^{\infty }f\left( x\right) | ||
\left( \partial_{x}\mathrm{e}^{-\mathrm{i}kx}\right) \mathrm{d}x \\ | \left( \partial_{x}\mathrm{e}^{-\mathrm{i}kx}\right) \mathrm{d}x \\ | ||
| − | &=& | + | &=&ik\int_{-\infty }^{\infty }f\left( x\right) \mathrm{e}^{-\mathrm{i}kx}\mathrm{d}x |
\end{matrix} | \end{matrix} | ||
</math></center> | </math></center> | ||
where we have assumed that the function <math>f\left( x\right) </math> vanishes at <math>\pm | where we have assumed that the function <math>f\left( x\right) </math> vanishes at <math>\pm | ||
\infty .</math> This means that the Fourier transform converts differentiation to | \infty .</math> This means that the Fourier transform converts differentiation to | ||
| − | multiplication by <math>k</math>. | + | multiplication by <math>i k</math>. |
==Solution for the Linearized KdV== | ==Solution for the Linearized KdV== | ||
| Line 47: | Line 43: | ||
equation | equation | ||
<center><math> | <center><math> | ||
| − | \partial _{t}u+\partial _{x}^{3}u=0,\ \ -\infty <x<\infty | + | \partial _{t}u+\partial _{x}^{3}u=0,\ \ -\infty < x <\infty |
</math></center> | </math></center> | ||
subject to solve initial conditions | subject to solve initial conditions | ||
| Line 63: | Line 59: | ||
Therefore | Therefore | ||
<center><math> | <center><math> | ||
| − | u\left( x,t\right) =\int_{ | + | u\left( x,t\right) = \frac{1}{2\pi} |
| + | \int_{-\infty}^{\infty }\hat{f}\left( k\right) | ||
\mathrm{e}^{\mathrm{i}k^{3}t}\mathrm{e}^{\mathrm{i}kx}\mathrm{d}k | \mathrm{e}^{\mathrm{i}k^{3}t}\mathrm{e}^{\mathrm{i}kx}\mathrm{d}k | ||
</math></center> | </math></center> | ||
| Line 69: | Line 66: | ||
==Numerical Implementation Using the FFT== | ==Numerical Implementation Using the FFT== | ||
| − | The Fast Fourier Transform (FFT) | + | The Fast Fourier Transform (FFT) is a method to calculate the fourier |
transform efficiently for discrete sets of points. These points need to be | transform efficiently for discrete sets of points. These points need to be | ||
evenly spaced in the <math>x</math> plane and are given by | evenly spaced in the <math>x</math> plane and are given by | ||
| Line 144: | Line 141: | ||
\mathrm{e}^{\mathrm{i}k^{3}\Delta t} \\ | \mathrm{e}^{\mathrm{i}k^{3}\Delta t} \\ | ||
\hat{u}\left( k,t+\Delta t\right) &=&\hat{u}_{1}\left( k,t+\Delta t\right) | \hat{u}\left( k,t+\Delta t\right) &=&\hat{u}_{1}\left( k,t+\Delta t\right) | ||
| − | + | -3ik \Delta t\widehat{\left( u_{1}^{2}\right)} | |
\end{matrix}</math></center> | \end{matrix}</math></center> | ||
Note that we are using Euler's method to time step and that the solution | Note that we are using Euler's method to time step and that the solution | ||
| Line 157: | Line 154: | ||
\mathrm{e}^{\mathrm{i}k^{3}\Delta t} \\ | \mathrm{e}^{\mathrm{i}k^{3}\Delta t} \\ | ||
\hat{u}\left( k,t+\Delta t\right) &=&\hat{u}_{1}\left( k,t+\Delta t\right) | \hat{u}\left( k,t+\Delta t\right) &=&\hat{u}_{1}\left( k,t+\Delta t\right) | ||
| − | - 3ik\Delta t\left( \mathcal{F}\left( \left( \mathcal{F}^{-1}\left[ u\right] | + | - 3ik\Delta t\left( \mathcal{F}\left( \left( \mathcal{F}^{-1}\left[ \hat{u}_{1}\left( k,t+\Delta t\right)\right] |
\right) ^{2}\right) \right) | \right) ^{2}\right) \right) | ||
\end{matrix}</math></center> | \end{matrix}</math></center> | ||
| Line 196: | Line 193: | ||
end | end | ||
| + | |||
| + | == Example Calculations == | ||
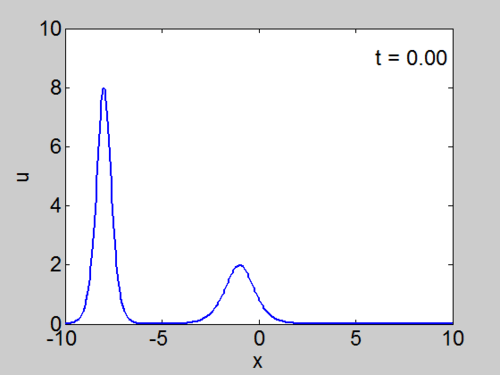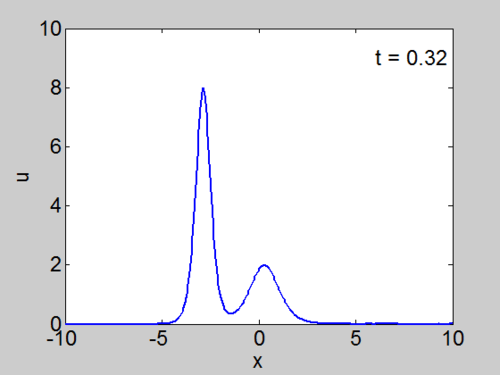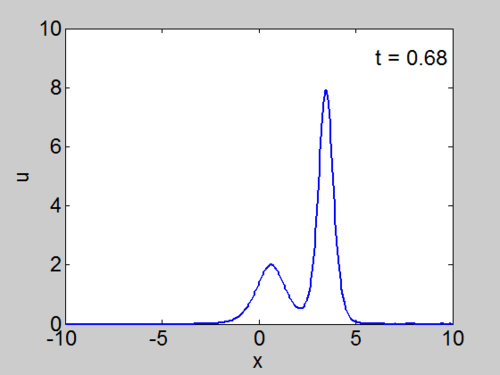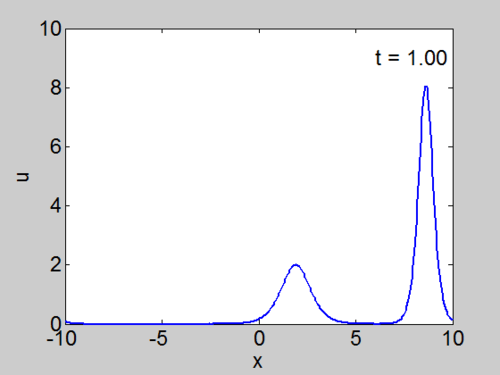
| + | We cosider the evolution of the KdV with two solitons as | ||
| + | initial condition as given below. | ||
| + | <center><math> | ||
| + | u(x,0) = 8\,\mathrm{sech}^{2}\left(2(x+8)\right) | ||
| + | + \, 2 \mathrm{sech}^{2}\left(\left( | ||
| + | x +1\right) \right)</math></center> | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | ! Animation | ||
| + | ! Three-dimensional plot. | ||
| + | |- | ||
| + | | [[Image:Two_soliton.gif|thumb|right|500px|Evolution of <math>u(x,t)</math> for two solitons.]] | ||
| + | | [[Image:Two_soliton.jpg|thumb|right|500px|Evolution of <math>u(x,t)</math> for two solitons. | ||
| + | Note the phase shift which occurs in the soliton interaction.]] | ||
| + | |||
| + | |} | ||
| + | |||
| + | |||
| + | == Lecture Videos == | ||
| + | |||
| + | === Part 1 === | ||
| + | |||
| + | {{#ev:youtube|ZjeuLNdxcRc}} | ||
| + | |||
| + | === Part 2 === | ||
| + | |||
| + | {{#ev:youtube|C7gI5PCKvFQ}} | ||
| + | |||
| + | === Part 3 === | ||
| + | |||
| + | {{#ev:youtube|X7-p8nBmKw4}} | ||
| + | |||
| + | === Part 4 === | ||
| + | |||
| + | {{#ev:youtube|xevnpuOoks0}} | ||
Latest revision as of 02:58, 17 August 2023
| Nonlinear PDE's Course | |
|---|---|
| Current Topic | Numerical Solution of the KdV |
| Next Topic | Conservation Laws for the KdV |
| Previous Topic | Introduction to KdV |
Introduction
We present here a method to solve the KdV equation numerically. There are many different methods to solve the KdV and we use here a spectral method which has been found to work well. Spectral methods work by using the Fourier transform (or some varient of it) to calculate the derivative.
Fourier Transform
Recall that the Fourier transform is given by
and the inverse Fourier transform is given by
(note that there are other ways of writing this transform). The most important property of the Fourier transform is that
where we have assumed that the function [math]\displaystyle{ f\left( x\right) }[/math] vanishes at [math]\displaystyle{ \pm \infty . }[/math] This means that the Fourier transform converts differentiation to multiplication by [math]\displaystyle{ i k }[/math].
Solution for the Linearized KdV
We begin with a simple example. Suppose we want to solve the linearized KdV equation
subject to solve initial conditions
We can solve this equation by taking the Fourier transform. and obtain
So that
Therefore
Numerical Implementation Using the FFT
The Fast Fourier Transform (FFT) is a method to calculate the fourier transform efficiently for discrete sets of points. These points need to be evenly spaced in the [math]\displaystyle{ x }[/math] plane and are given by
(note they can start at any [math]\displaystyle{ x }[/math] value). For the FFT to be as efficient as possible [math]\displaystyle{ N }[/math] should be a power of [math]\displaystyle{ 2. }[/math] Corresponding to the discrete set of points in the [math]\displaystyle{ x }[/math] domain is a discrete set of points in the [math]\displaystyle{ k }[/math] plane given by
where [math]\displaystyle{ \Delta k=2\pi /(N\Delta x). }[/math] Note that this numbering seems slighly odd and is due to aliasing. We are not that interested in the frequency domain solution but we need to make sure that we select the correct values of [math]\displaystyle{ k }[/math] for our numerical code.
Numerical Code for the Linear KdV
Here is the code to solve the linear KdV using MATLAB
N = 1024;
t=0.1;
x = linspace(-10,10,N);
delta_x = x(2) - x(1);
delta_k = 2*pi/(N*delta_x);
k = [0:delta_k:N/2*delta_k,-(N/2-1)*delta_k:delta_k:-delta_k];
f = exp(-x.^2);
f_hat = fft(f);
u = real(ifft(f_hat.*exp(i*k.^3*t)));
Numerical Solution of the KdV
It turns out that a method to solve the KdV equation can be derived using spectral methods. We begin with the KdV equation written as
The Fourier transform of the KdV is therefore
We solve this equation by a split step method. We write the equation as
We can solve
exactly while the equation
needs to be solved by time stepping. The idea of the split step method is to solve alternatively each of these equations when stepping from [math]\displaystyle{ t }[/math] to [math]\displaystyle{ t+\Delta t. }[/math] Therefore we solve
Note that we are using Euler's method to time step and that the solution could be improved by using a better method, such as the Runge-Kutta 4 method.
The only slighly tricky thing is that we have both [math]\displaystyle{ u }[/math] and [math]\displaystyle{ \hat{u} }[/math] in the equation, but we can simply use the Fourier transform to connect these. The equation then becomes
Numerical Code to solve the KdV by the split step method
Here is some code to solve the KdV using MATLAB
N = 256;
x = linspace(-10,10,N);
delta_x = x(2) - x(1);
delta_k = 2*pi/(N*delta_x);
k = [0:delta_k:N/2*delta_k,-(N/2-1)*delta_k:delta_k:-delta_k];
c=16;
u = 1/2*c*(sech(sqrt(c)/2*(x+8))).^2;
delta_t = 0.4/N^2;
tmax = 0.1; nmax = round(tmax/delta_t);
U = fft(u);
for n = 1:nmax
% first we solve the linear part
U = U.*exp(1i*k.^3*delta_t);
%then we solve the non linear part
U = U - delta_t*(3i*k.*fft(real(ifft(U)).^2));
end
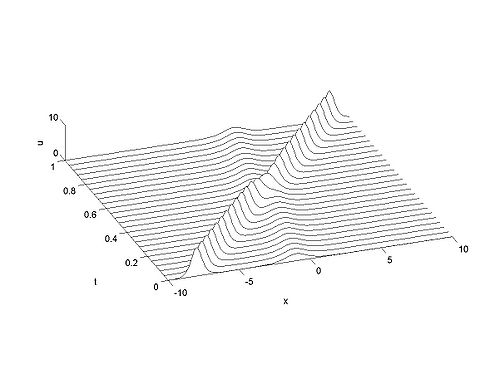
Example Calculations
We cosider the evolution of the KdV with two solitons as initial condition as given below.
| Animation | Three-dimensional plot. |
|---|---|