Difference between revisions of "Introduction to KdV"
| (10 intermediate revisions by the same user not shown) | |||
| Line 48: | Line 48: | ||
where <math>A</math> is a constant of integration. | where <math>A</math> is a constant of integration. | ||
| − | If think about this equation as Newton's second law in a potential well <math> | + | If we think about this equation as Newton's second law in a potential well <math> |
| − | V(f) </math> | + | V(f) </math> then the equation is |
<center><math> | <center><math> | ||
\frac{\mathrm{d}^{2}f}{\mathrm{d}\zeta^{2}}= -\frac{\mathrm{d}V}{\mathrm{d}f} | \frac{\mathrm{d}^{2}f}{\mathrm{d}\zeta^{2}}= -\frac{\mathrm{d}V}{\mathrm{d}f} | ||
| Line 69: | Line 69: | ||
f^{^{\prime }}=v.</math> This gives us | f^{^{\prime }}=v.</math> This gives us | ||
<center><math>\begin{matrix} | <center><math>\begin{matrix} | ||
| − | \frac{\mathrm{d} | + | \frac{\mathrm{d}f}{\mathrm{d}\zeta} &=&v \\ |
| − | \frac{\mathrm{d} | + | \frac{\mathrm{d}v}{\mathrm{d}\zeta} &=&A_{1}+cf-3f^{2} |
\end{matrix}</math></center> | \end{matrix}</math></center> | ||
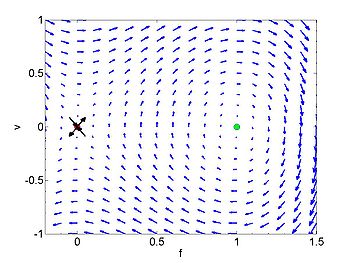
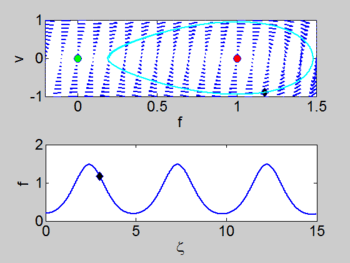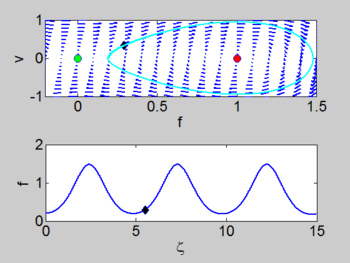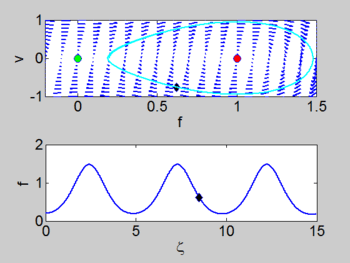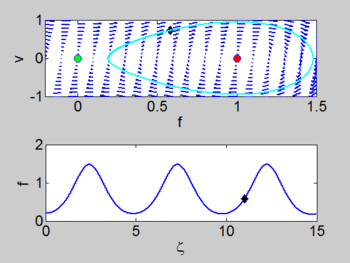
If we chose <math>A_{1}=0</math> then we obtain two equilibria at <math>(f,v)=\left( | If we chose <math>A_{1}=0</math> then we obtain two equilibria at <math>(f,v)=\left( | ||
0,0\right) </math> and <math>(3/c,0).</math> If we analysis these equilibria we find the | 0,0\right) </math> and <math>(3/c,0).</math> If we analysis these equilibria we find the | ||
first is a saddle and the second is a nonlinear center (it is neither repelling nor | first is a saddle and the second is a nonlinear center (it is neither repelling nor | ||
| − | attracting). There is a | + | attracting). |
| + | The Jacobian matrix for the saddle point is | ||
| + | <center><math> | ||
| + | J_{\left( 0,0\right) }=\left( | ||
| + | \begin{array}{cc} | ||
| + | 0 & 1 \\ | ||
| + | c & 0 | ||
| + | \end{array} | ||
| + | \right) | ||
| + | </math></center> | ||
| + | which has eigenvalues at <math>\pm \sqrt{c}</math> and the incident directions are | ||
| + | <center><math> | ||
| + | \left( | ||
| + | \begin{array}{c} | ||
| + | 1\\ | ||
| + | \sqrt{c} | ||
| + | \end{array} | ||
| + | \right) \leftrightarrow \sqrt{c},\left( | ||
| + | \begin{array}{c} | ||
| + | -1 \\ | ||
| + | \sqrt{c} | ||
| + | \end{array} | ||
| + | \right) \leftrightarrow -\sqrt{c} | ||
| + | </math></center> | ||
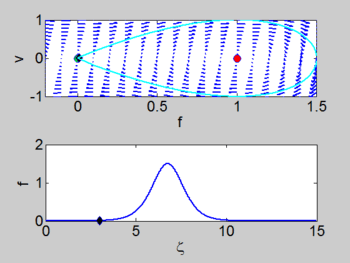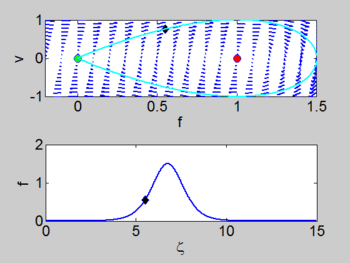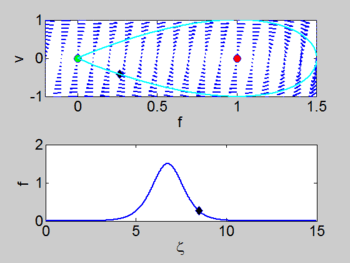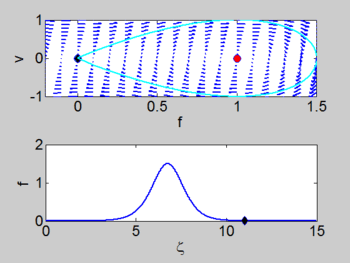
| + | There is a | ||
homoclinic connection which connects the equilibrium point at the origin. This holoclinic | homoclinic connection which connects the equilibrium point at the origin. This holoclinic | ||
connection represents the solitary wave. Within this homoclinic connection | connection represents the solitary wave. Within this homoclinic connection | ||
lie periodic orbits which represent the cnoidal waves. | lie periodic orbits which represent the cnoidal waves. | ||
| − | + | {| class="wikitable" | |
| + | |- | ||
| + | ! Phase portrait | ||
| + | ! Solitary Wave | ||
| + | ! Cnoidal Wave | ||
| + | |- | ||
| + | | [[Image:Kdv phase portrait.jpg|thumb|350px|Phase portrait]] | ||
| + | | [[Image:Kdv wave solitary2.gif|thumb|350px|Solitary Wave]] | ||
| + | | [[Image:Kdv wave cn.gif|thumb|350px|Cnoidal Wave]] | ||
| + | |} | ||
We can also integrate the equation | We can also integrate the equation | ||
<center><math> | <center><math> | ||
| − | -cf+3f^{2}+\frac{\mathrm{d}^{2}f}{\mathrm{d} | + | -cf+3f^{2}+\frac{\mathrm{d}^{2}f}{\mathrm{d}\zeta^{2}}=A_{1} |
</math></center> | </math></center> | ||
by multiplying by <math>f^{\prime }</math>and integrating. This gives us | by multiplying by <math>f^{\prime }</math>and integrating. This gives us | ||
| Line 97: | Line 130: | ||
This is a separable equation and the only challenge is to integrate | This is a separable equation and the only challenge is to integrate | ||
<center><math> | <center><math> | ||
| − | \int \frac{1}{\sqrt{- | + | \int \frac{1}{\sqrt{-2V(f)}} \mathrm{d}f. |
</math></center> | </math></center> | ||
| Line 132: | Line 165: | ||
This gives us | This gives us | ||
<center><math> | <center><math> | ||
| − | -\frac{2}{\sqrt{ | + | -\frac{2}{\sqrt{c}}s=\zeta+a |
</math></center> | </math></center> | ||
Therefore | Therefore | ||
| Line 149: | Line 182: | ||
[http://en.wikipedia.org/wiki/John_Scott_Russell John Scott Russell]. | [http://en.wikipedia.org/wiki/John_Scott_Russell John Scott Russell]. | ||
| − | ==Formula for the | + | ==Formula for the cnoidal wave== |
| − | If we consider the case when the solution oscillates between two values <math>F_2<F_3</math> | + | If we consider the case when the solution oscillates between two values <math>F_2 < F_3</math> |
(which we can assume are also roots of <math>V(f)</math> without loss of generality) then | (which we can assume are also roots of <math>V(f)</math> without loss of generality) then | ||
we can integrate the equation to obtain | we can integrate the equation to obtain | ||
| Line 169: | Line 202: | ||
In the limit the two solutions agree. We also obtain a sinusoidal solution in the limit of | In the limit the two solutions agree. We also obtain a sinusoidal solution in the limit of | ||
small amplitude. | small amplitude. | ||
| + | |||
| + | == Lecture Videos == | ||
| + | |||
| + | === Part 1 === | ||
| + | |||
| + | {{#ev:youtube|SzZ-KhvvPio}} | ||
| + | |||
| + | === Part 2 === | ||
| + | |||
| + | {{#ev:youtube|QltlSQQBtrs}} | ||
| + | |||
| + | === Part 3 === | ||
| + | |||
| + | {{#ev:youtube|NJ7h3Z9QtvU}} | ||
| + | |||
| + | === Part 4 === | ||
| + | |||
| + | {{#ev:youtube|NictSlSgRbM}} | ||
Latest revision as of 03:57, 10 August 2023
| Nonlinear PDE's Course | |
|---|---|
| Current Topic | Introduction to KdV |
| Next Topic | Numerical Solution of the KdV |
| Previous Topic | Nonlinear Shallow Water Waves |
The KdV (Korteweg-De Vries) equation is one of the most important non-linear pde's. It was originally derived to model shallow water waves with weak nonlinearities, but it has a wide variety of applications. The derivation of the KdV is given in KdV Equation Derivation. The KdV equation is written as
More information about it can be found at Korteweg de Vries equation
Travelling Wave Solution
The KdV equation posesses travelling wave solutions. One particular travelling wave solution is called a soltion and it was discovered experimentally by John Scott Russell in 1834. However, it was not understood theoretically until the work of Korteweg and de Vries in 1895.
We begin with the assumption that the wave travels with contant form, i.e. is of the form
Note that in this equation the parameter [math]\displaystyle{ c }[/math] is an unknown as is the function [math]\displaystyle{ f. }[/math] Only very special values of [math]\displaystyle{ c }[/math] and [math]\displaystyle{ f }[/math] will give travelling waves. We introduce the coordinate [math]\displaystyle{ \zeta = x - ct }[/math]. If we substitute this expression into the KdV equation we obtain
We can integrate this with respect to [math]\displaystyle{ \zeta }[/math] to obtain
where [math]\displaystyle{ A }[/math] is a constant of integration.
If we think about this equation as Newton's second law in a potential well [math]\displaystyle{ V(f) }[/math] then the equation is
then the potential well is given by
Therefore our equation for [math]\displaystyle{ f }[/math] may be thought of as the motion of a particle in a cubic well.
The constant [math]\displaystyle{ A_0 }[/math] has no effect on our solution so we can set it to be zero. We can choose the constant [math]\displaystyle{ A_{1}=0 }[/math] and then we have a maximum at [math]\displaystyle{ f=0 }[/math]. There is a solution which rolls from this at [math]\displaystyle{ t=-\infty }[/math] and then runs up the other side and finally returns to the maximum at [math]\displaystyle{ t=\infty . }[/math] This corresponds to a solitary wave solution.
We can also think about the equation as a first order system using [math]\displaystyle{ f^{^{\prime }}=v. }[/math] This gives us
If we chose [math]\displaystyle{ A_{1}=0 }[/math] then we obtain two equilibria at [math]\displaystyle{ (f,v)=\left( 0,0\right) }[/math] and [math]\displaystyle{ (3/c,0). }[/math] If we analysis these equilibria we find the first is a saddle and the second is a nonlinear center (it is neither repelling nor attracting). The Jacobian matrix for the saddle point is
which has eigenvalues at [math]\displaystyle{ \pm \sqrt{c} }[/math] and the incident directions are
There is a homoclinic connection which connects the equilibrium point at the origin. This holoclinic connection represents the solitary wave. Within this homoclinic connection lie periodic orbits which represent the cnoidal waves.
| Phase portrait | Solitary Wave | Cnoidal Wave |
|---|---|---|
We can also integrate the equation
by multiplying by [math]\displaystyle{ f^{\prime } }[/math]and integrating. This gives us
It is no coincidence that the right hand side is the potential energy, because this is nothing more that the equation for conservation of energy (or the first integral of the Lagrangian system) which does not depend on [math]\displaystyle{ \zeta }[/math].
This is a separable equation and the only challenge is to integrate
Formula for the solitary wave
We know that the solitary wave solution is found when [math]\displaystyle{ A_{0}=A_{1}=0. }[/math] This gives us
This can be solved by separation of variables to give
We then substitute
and note that
and that
This means that
This gives us
Therefore
Of course we assumed that [math]\displaystyle{ x=x-ct }[/math] so the formula for the solitary wave is given by
Note that a solution exists for each [math]\displaystyle{ c }[/math], and that the amplitude is proportional to [math]\displaystyle{ c. }[/math] All of this was discovered experimentally by John Scott Russell.
Formula for the cnoidal wave
If we consider the case when the solution oscillates between two values [math]\displaystyle{ F_2 \lt F_3 }[/math] (which we can assume are also roots of [math]\displaystyle{ V(f) }[/math] without loss of generality) then we can integrate the equation to obtain
where [math]\displaystyle{ cn }[/math] is a Jacobi Elliptic function and [math]\displaystyle{ \gamma }[/math] and [math]\displaystyle{ k }[/math] are constants which depend on [math]\displaystyle{ c }[/math]. Derivation of this equation is found KdV Cnoidal Wave Solutions. We can write this equation as
where [math]\displaystyle{ a=k^2\gamma^2 }[/math] and [math]\displaystyle{ c = 6b + 4(2k^2 -1)\gamma^2 }[/math]. These waves are known as cnoidal waves.
In the limit the two solutions agree. We also obtain a sinusoidal solution in the limit of small amplitude.