Difference between revisions of "Linear Wave-Body Interaction"
| (147 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | {{Ocean Wave Interaction with Ships and Offshore Structures | |
| − | + | | chapter title = Linear Wave-Body Interaction | |
| + | | next chapter = [[Long Wavelength Approximations]] | ||
| + | | previous chapter = [[Ship Kelvin Wake]] | ||
| + | }} | ||
| − | + | {{incomplete pages}} | |
| − | + | [[Image:Rigid_body.jpg|thumb|right|600px|Rigid body motions]] | |
| − | + | We consider a [[Linear Plane Progressive Regular Waves|Linear Plane Progressive Regular Wave]] in the | |
| + | [[Frequency Domain Problem|Frequency Domain]] interacting with a floating body in two dimensions (the main concepts survive almost with no change in the more practical three-dimensional problem). | ||
| − | + | == Introduction == | |
| − | + | We derive here the equations of motion for a body in [[Linear Plane Progressive Regular Waves]] in the frequency domain in | |
| + | two dimensions. We begin with the equations in the time domian. The simplest problems is [[Waves reflecting off a vertical wall]] | ||
| − | + | == Equations for a Floating Body in the Time Domain == | |
| − | |||
| − | + | We begin with the equations for a floating two-dimensional body in the time domain. | |
| − | + | {{equations of motion time domain without body condition}} | |
| − | + | {{two dimensional floating body time domain}} | |
| − | + | More details can be found in [[:Category:Time-Dependent Linear Water Waves|Time-Dependent Linear Water Waves]] | |
| − | + | == Equations for a Floating Body in the Frequency Domain == | |
| − | + | The dynamic condition is the equation of motion for the structure in the [[Frequency Domain Problem|frequency domain]] | |
| + | can be found from the time domain equations and we introduce the following notation | ||
| + | <center><math> | ||
| + | \xi_{\nu} = \zeta_{\nu}e^{-\mathrm{i}\omega t}\, | ||
| + | </math></center> | ||
| + | This give us | ||
| + | {{standard linear wave scattering equations without body condition}} | ||
| + | <center><math> | ||
| + | -\omega^2 \sum_{\nu} M_{\mu\nu}\zeta_{\nu}=\mathrm{i}\omega\rho\iint_{\partial\Omega}\phi n_{\mu}\, \mathrm{d}S | ||
| + | - \sum_{\nu} C_{\mu\nu}\zeta_{\nu},\quad \textrm{for} \qquad \mu=1,3,5, | ||
| + | </math></center> | ||
| + | The equations of motion for <math> \zeta_\nu\,</math> follow from Newton's law applied to each mode in two dimensions. The same principles apply with very minor changes in three dimensions. We use the standard numbering of the modes of motion. | ||
| − | + | == Equations for a Fixed Body in Frequency Domain == | |
| − | + | The equations for a fixed body are | |
| − | + | {{standard linear wave scattering equations without body condition}} | |
| + | {{frequency domain equations for a rigid body}} | ||
| + | plus the radiation conditions. | ||
| − | + | We decompose the potential as | |
| + | <math> | ||
| + | \phi = \phi^{\mathrm{I}} + \phi^{\mathrm{D}} \,, | ||
| + | </math> | ||
| + | where <math>\phi^{\mathrm{I}}</math> is the incident potential and <math>\phi^{\mathrm{D}}</math> | ||
| + | is the diffracted potential. The boundary condition for the diffracted potential is | ||
| + | <center><math> | ||
| + | \begin{align} | ||
| + | \Delta\phi^{\mathrm{D}}&=0, &-h<z<0,\,\,\mathbf{x} \in \Omega \\ | ||
| + | \partial_n\phi^{\mathrm{D}} &= 0, &z=-h, \\ | ||
| + | \partial_n \phi^{\mathrm{D}} &= \alpha \phi, &z=0,\,\,\mathbf{x} \in \partial\Omega_{F}, | ||
| + | \end{align} | ||
| + | </math></center> | ||
| + | plus | ||
| + | <center><math> | ||
| + | \partial_n \phi^{\mathrm{D}} = - \partial_n \phi^{\mathrm{I}},\,\, \mathbf{x} \in \partial\Omega_{B}, | ||
| + | </math></center> | ||
| − | + | Code to calculate the solution (using a slighly modified method) can be found in | |
| + | [[Boundary Element Method for a Fixed Body in Finite Depth]] | ||
| − | + | == Equations for the Radiation Potential in Frequency Domain == | |
| − | + | We decompose the body motion into the rigid body modes of motion. Associated with | |
| + | each of these modes is a potential which must be solved for. | ||
| + | The equations for the radiation potential in the frequency domain are | ||
| − | + | {{standard linear wave scattering equations without body condition}} | |
| + | {{frequency domain equations for the radiation modes}} | ||
| − | + | {{sommerfeld radiation condition two dimensions for radiation}} | |
| − | + | Code to calculate the radiation potential can be found in | |
| + | [[Boundary Element Method for the Radiation Potential in Finite Depth]] | ||
| − | + | We denote the solution for each of the radiation potentials by | |
| + | <math>\phi_\nu^{\mathrm{R}}</math> and the total potential is written as | ||
| + | <center><math> | ||
| + | \phi = \phi^{\mathrm{I}} + \phi^{\mathrm{D}} - \mathrm{i} \omega | ||
| + | \sum_\nu \zeta_\nu \phi_\nu^{\mathrm{R}} | ||
| + | </math> | ||
| + | </center> | ||
| − | + | == Final System of Equations == | |
| − | + | We substitute the expansion for the potential into the equations in the frequency domain and we obtain | |
| + | <center><math> | ||
| + | -\omega^2 \sum_{\nu} M_{\mu\nu}\zeta_{\nu}=\mathrm{i}\omega\rho\iint_{\partial\Omega_{B}} | ||
| + | \left(\phi^{\mathrm{I}} + \phi^{\mathrm{D}} - \mathrm{i}\omega | ||
| + | \sum_{\nu} \zeta_\nu \phi_{\nu}^{\mathrm{R}}\right) \mathbf{n}_{\mu}\, dS | ||
| + | - \sum_{\nu} C_{\mu\nu}\xi_{\nu},\quad \textrm{for} \qquad \mu=1,3,5, | ||
| + | </math></center> | ||
| − | + | {{added mass damping and force matrices definition}} | |
| − | <center><math> \mathbf{M} \ | + | Then the equations can be expressed as follows. |
| + | <center><math> \left[-\omega^2 \left(\mathbf{M} + \mathbf{A} \right) - | ||
| + | \mathrm{i}\omega \mathbf{B} + \mathbf{C} \right] \vec{\zeta} = \mathbf{f} </math></center> | ||
| + | where <math>\mathbf{M}</math> is the mass matrix, <math>\mathbf{A}</math> is the added mass matrix, | ||
| + | <math>\mathbf{B}</math> is the damping matrix, <math>\mathbf{C}</math> is the hydrostatic matrix, | ||
| + | <math>\vec{\zeta}</math> is the vector of body displacements and <math>\mathbf{f}</math> is the force. | ||
| − | |||
| − | + | The extension of these equations to six degrees of freedom is straightforward. However before discussing the general case we will study specific properties of the two dimensional problem for the sake of clarity. | |
| − | + | == Symmetric body == | |
| − | + | For a body which is [[:Category:Symmetry in Two Dimensions|Symmetric in Two Dimensions]] | |
| + | the Heave is decoupled from Surge and Roll. | ||
| + | In other words the Surge and Roll motions do not influence Heave and vice versa. | ||
| − | + | == Matlab Code == | |
| − | |||
| − | + | *A program to solve for pitch and heave and only for two geometries can be found here [http://www.math.auckland.ac.nz/~meylan/code/boundary_element/rigid_body_motion.m rigid_body_motion.m] | |
| − | + | * a program to calculate the solution for a specific geometry (with plot as output as shown) can be found here [http://www.math.auckland.ac.nz/~meylan/code/boundary_element/wave_bem_example_floating.m wave_bem_example_floating.m] | |
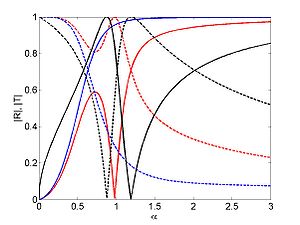
| − | + | [[Image:Wave_bem_example_floating_RT2.jpg|300px|right|thumb|The reflection (solid line) and transmission (dashed line) | |
| + | for a dock for heave and pitch (red), heave only (blue) and pitch only (black)]] | ||
| − | + | === Additional code === | |
| − | + | This program requires | |
| + | * A program to calculate the geometery [http://www.math.auckland.ac.nz/~meylan/code/boundary_element/circlebody_twod.m circlebody_twod.m] | ||
| + | * {{fixed body bem code}} | ||
| + | * {{floating body radiation code}} | ||
| + | * {{free surface dispersion equation code}} | ||
| + | * {{boundary element code}} | ||
| − | + | == Symmetry-reciprocity relations == | |
| − | <center><math> | + | It will be shown that |
| + | <center><math> A_{ij}(\omega) = A_{ji}(\omega) \,</math></center> | ||
| + | <center><math> B_{ij}(\omega) = B_{ji}(\omega) \,</math></center> | ||
| + | Along the same lines it will be shown that the exciting force <math>\mathbf{X}_j\,</math> can be expressed in terms of <math> \psi_j\,</math> circumventing the solution for the diffraction potential. | ||
| + | The core result needed for the proof of the above properties is [http://en.wikipedia.org/wiki/Green's_identities Green's second identity] | ||
| + | <center><math> \iint_S \left( \psi_1 \frac{\partial\psi_2}{\partial n} - \psi_2 \frac{\partial\psi_1}{\partial n} \right) \mathrm{d}S = 0 \,</math></center> | ||
| + | where <math>\nabla^2 \psi_i=0</math>. | ||
| − | + | {{energy_region_plates}} | |
| − | + | [[Image:Symmetry_boundary.jpg|thumb|right|600px|Boundary]] | |
| − | + | In the surface wave-body problem define the closed surfaces as shown in figure on the right. | |
| + | Let <math> \phi_j\,</math> be rediation or diffraction potentials. Over the boundaries <math>S^\pm\,</math> we have: | ||
| − | + | <center><math> S^+: \quad \phi_j \ \sim \ \frac{igA_j^+}{\omega} e^{Kz-iKx} \,</math></center> | |
| − | <center><math> | + | <center><math> \frac{\partial\phi_j}{\partial n} = \frac{\partial \phi_j}{\partial x} \ \sim \ -iK\phi_j \,</math></center> |
| − | + | <center><math> S^-: \quad \phi_j \ \sim \ \frac{igA_j^-}{\omega} e^{Kz+iKx} \,</math></center> | |
| − | + | <center><math> \frac{\partial\phi_j}{\partial n} = - \frac{\partial \phi_j}{\partial x} \ \sim \ - iK\phi_j \,</math></center> | |
| − | < | + | On <math> S_F: \qquad \frac{\partial\phi_j}{\partial z} = K\phi_j, \qquad \frac{\partial \Phi_j}{\partial n} = \frac{\partial \phi_j}{\partial z} </math> |
| − | + | On <math> S_\infty: \qquad \left| \phi_j \right|, \quad \left| \nabla \phi_j \right| \to 0 </math>. | |
| − | < | + | Applying Green's identity to any pair of the radiation potentials <math> \psi_i, \psi_j \,</math>: |
| − | <center><math> \ | + | <center><math> \iint_{S_B} \left[ \psi_i \frac{\partial\psi_j}{\partial n} - \psi_j \frac{\partial\psi_i}{\partial n} \right] \mathrm{d}S = - \iint_{S_F} \left[ \psi_i \frac{\partial\psi_j}{\partial z} - \psi_j \frac{\partial\psi_i}{\partial z} \right] \mathrm{d}S </math></center> |
| − | < | + | <center><math> - \iint_{S_+} \left[ \psi_i \frac{\partial\psi_j}{\partial x} - \psi_j \frac{\partial\psi_i}{\partial x} \right] \mathrm{d}S |
| + | + \iint_{S_-} \left[ \psi_i \frac{\partial\psi_j}{\partial x} - \psi_j \frac{\partial\psi_i}{\partial x} \right] \mathrm{d}S = 0 </math></center> | ||
| − | + | It follows that: | |
| − | + | <center><math> \iint_{S_B} \psi_i \frac{\partial\psi_j}{\partial n} \mathrm{d}S = \iint_{S_B} \psi_j \frac{\partial\psi_i}{\partial n} \mathrm{d}S </math></center> | |
| + | or | ||
| + | <center><math> A_{ij}(\omega) = A_{ji}(\omega), \qquad B_{ij}(\omega) = B_{ji}(\omega). \,</math></center> | ||
| − | + | == Haskind relations of exciting forces == | |
| − | + | <center><math> | |
| + | \begin{align} | ||
| + | \mathbf{X}_i(\omega) &= - i\omega\rho\iint_{S_B} (\phi_I + \phi_7) n_i \mathrm{d}S \\ | ||
| + | &= - \rho \iint_{S_B} (\phi_I + \phi_7) \frac{\partial \phi_i}{\partial n} \mathrm{d}S | ||
| + | \end{align} | ||
| + | </math></center> | ||
| − | + | where the radiation velocity potential <math> \phi_i \,</math> is known to satisfy: | |
| − | + | <center><math> \frac{\partial\phi_i}{\partial n} = i\omega n_i, \quad \mbox{on} \ S_B </math></center> | |
| − | + | and | |
| − | + | <center><math> \frac{\partial\phi_7}{\partial n} = \frac{\partial\phi_I}{\partial n}, \quad \mbox{on} \ S_B </math></center> | |
| − | + | Both <math> \phi_i\,</math> and <math> \phi_7\,</math> satisfy the condition of outgoing waves at infinity. By virtue of [http://en.wikipedia.org/wiki/Green's_identities Green's second identity] | |
| − | < | + | <center><math> \iint_{S_B} \phi_7 \frac{\partial\phi_i}{\partial n} \mathrm{d}S = \iint_{S_B} \phi_i \frac{\partial\phi_7}{\partial n} \mathrm{d}S = -\iint_{S_B} \phi_i \frac{\partial\phi_I}{\partial n} \mathrm{d}S </math></center> |
| − | + | The Haskind expression for the exciting force follows: | |
| − | + | <center><math> \mathbf{X}_i(\omega) = \rho \iint_{S_B} \left[ \phi_I \frac{\partial\phi_i}{\partial n} - \phi_i \frac{\partial\phi_I}{\partial n} \right] \mathrm{d}S </math></center> | |
| − | + | The symmetry of the <math> A_{ij}(\omega), B_{ij}(\omega) \,</math> matrices applies in 2D and 3D. The application of Green's Theorem in 3D is very similar using the far-field representation for the potential <math> \phi_j\,</math> | |
| − | + | <center><math> \phi_j \sim \frac{A_j(\theta)}{\sqrt{R}} e^{KZ-iKR} + O\left(\frac{1}{R^{3/2}}\right) </math></center> | |
| − | + | <center><math> \frac{\partial\phi_j}{\partial n} = \frac{\partial\phi_j}{\partial R} \sim - i K \phi_j + O\left(\frac{1}{R^{3/2}}\right) </math></center> | |
| − | + | where <math> R \,</math> is a radius from the body out to infinity and the <math> R^{-\frac{1}{2}} \,</math> decay arises from the energy conservation principle. Details of the 3D proof may be found in [[Mei 1983]] and [[Wehausen and Laitone 1960]] | |
| − | + | The use of the Haskind relations for the exciting forces does not require the solution of the diffraction problem. This is convenient and often more accurate. | |
| − | + | The Haskind relations take other forms which will not be presented here but are detailed in [[Wehausen and Laitone 1960]]. The ones that are used in practice relate the exciting forces to the damping coefficients. | |
| − | + | These take the form: | |
| − | < | + | <u>2D</u>: <math> B_{ii} = \frac{\left| \mathbf{X}_i \right|^2}{2\rho g V_g}, \quad V_g = \frac{g}{2\omega}, </math> Deep water |
| − | |||
| − | < | + | <u>3D</u>: <math> B_{33} = \frac{K}{4\rho g V_g} \left| \mathbf{X}_3 \right|^2 \,</math> --- Heave |
| + | (Axisymmetric bodies) <math> B_{22} = \frac{K}{8\rho g V_g} \left| \mathbf{X}_2 \right|^2 \,</math> --- Sway | ||
| − | [ | + | So knowledge of <math> \mathbf{X}_i(\omega)\,</math> allows the direct evaluation of the diagonal damping coefficients. These expressions are useful in deriving theoretical results in wave-body interactions to be discussed later. |
| + | |||
| + | The two-dimensional theory of wave-body interactions in the frequency domain extends to three dimencions very directly with little difficulty. | ||
| + | |||
| + | The statement of the 6 d.o.f. seakeeping problem is: | ||
| + | |||
| + | <center><math> \sum_{j=1}^6 \left[ - \omega^2 \left( M_{ij} + A_{ij} \right) + i \omega B_{ij} + C_{ij} \right] \Pi_j = \mathbf{X}_j, \quad i=1,\cdots,6 </math></center> | ||
| + | |||
| + | where | ||
| + | |||
| + | <center><math> M_{ij}: \mbox{Body inertia matrix including moments of inertia for rotational modes. For details refer to MH} \, </math></center> | ||
| + | |||
| + | <center><math> A_{ij}(\omega): \mbox{Added mass matrix} \,</math></center> | ||
| + | |||
| + | <center><math> B_{ij}(\omega): \mbox{Damping matrix} \, </math></center> | ||
| + | |||
| + | <center><math> C_{ij}: \mbox{Hydrostatic and static inertia restoring matrix. For details refer to MH} \, </math></center> | ||
| + | |||
| + | <center><math> \mathbf{X}_i(\omega): \mbox{Wave exciting forces and moments} </math></center> | ||
| + | |||
| + | At zero speed the definitions of the added-mass, damping matrices and exciting forces are identical to those in two dimensions. | ||
| + | |||
| + | The boundary value problems satisfied by the radiation potentials <math>\phi_j, \ j=1,\cdots,6 \,</math> and the diffraction potential <math> \phi_7 \,</math> are as follows: | ||
| + | |||
| + | Free-surface condition: | ||
| + | |||
| + | <center><math> -\omega^2 \phi_j + g \frac{\partial\phi_j}{\partial Z} = 0, \quad z=0 \quad j=1,\cdots,7 </math></center> | ||
| + | |||
| + | Body-boundary conditions: | ||
| + | |||
| + | <center><math> | ||
| + | \begin{align} | ||
| + | \frac{\partial\phi_7}{\partial n} &= -\frac{\partial\phi_I}{\partial n}, \quad \mbox{on} \quad S_B \\ | ||
| + | \phi_I &= \frac{i g A}{\omega} e^{Kz-iKx\cos\beta-iKy\sin\beta+i\omega t} \\ | ||
| + | \frac{\partial\phi_j}{\partial n} &= i\omega n_j, \quad j=1,\cdots,6 \, \\ | ||
| + | n_j &= \begin{cases} | ||
| + | n_j, & j=1,2,3 \\ | ||
| + | \left( \vec{x} \times \vec{n} \right), & j=4,5,6 | ||
| + | \end{cases} | ||
| + | \end{align} | ||
| + | </math></center> | ||
| + | |||
| + | <center><math> j=1: \ \mbox{Surge} \qquad j=2: \ \mbox{Sway} \qquad j=3: \ \mbox{Heave} </math></center> | ||
| + | <center><math> j=4: \ \mbox{Roll} \qquad j=5: \ \mbox{Pitch} \qquad j=6: \ \mbox{Yaw} </math></center> | ||
| + | |||
| + | At large distances from the body the velocity potentials satisfy the radiation condition: | ||
| + | |||
| + | <center><math> \phi_j (R,\theta) \sim \frac{A_j(\theta)}{\sqrt{R}} e^{Kz-iKR} + O \left( \frac{1}{R^{3/2}} \right) </math></center> | ||
| + | |||
| + | with | ||
| + | |||
| + | <center><math> K = \frac{\omega^2}{g}. \,</math></center> | ||
| + | |||
| + | This radiation condition is essential for the formulation and solution of the boundary value problems for <math>\phi_j\,</math> using panel methods which are the standard solution technique at zero and forward speed. | ||
| + | |||
| + | Qualitative behaviour of the forces, coefficients and motions of floating bodies | ||
| + | |||
| + | <center><math> - \omega^2 \phi + g \phi_Z =0 \quad \begin{cases} | ||
| + | \phi_Z=0,\quad \omega=0 \\ | ||
| + | \phi=0, \quad \omega \to \infty | ||
| + | \end{cases} </math></center> | ||
| + | |||
| + | <center><math> B_{33}(\omega), \sim \omega, \mbox{at low} \ \omega \,</math></center> | ||
| + | |||
| + | The 2D Heave added mass is singular at low frequencies. It is finite in 3D | ||
| + | |||
| + | The 2D Heave damping coefficient is decaying to zero linearly in 2D and superlinearly in 3D. A two-dimensional section is a better wavemaker than a three-dimensional one | ||
| + | |||
| + | A 2D section oscillating in Sway is less effective a wavemaker at low frequencies than the same section oscillating in Heave | ||
| + | |||
| + | The zero-frequency limit of the Sway added mass is finite and similar to the infinite frequency limit of the Heave added mass. | ||
| + | |||
| + | In long waves the Heave exciting force tends to the Heave restoring coefficient times the ambient wave amplitude the free surface behaves like a flat surface moving up and down. | ||
| + | |||
| + | In long waves the Sway exciting force tends to zero. Proof will follow | ||
| + | |||
| + | In short waves all forces tend to zero. | ||
| + | |||
| + | Pitch exciting moment (same applies to Roll) tends to zero. Long waves have a small slope which is proportional to <math> KA</math>, where <math> K\,</math> is the wave number and <math> A\,</math> is the wave amplitude. | ||
| + | |||
| + | Prove that to leading order for <math>KA\to 0 \,</math>: | ||
| + | |||
| + | <center><math> \left| X_S(\omega) \right| \sim KA C_{55}\,</math></center> | ||
| + | |||
| + | where <math>C_{55}\,</math> is the Pitch (<math> C_{44} \,</math> for Roll) hydrostatic restoring coefficient. [NB: very long waves look like a flat surface inclined at <math> KA\,</math> ]. | ||
| + | |||
| + | == Body motions in regular waves == | ||
| + | |||
| + | Heave: | ||
| + | |||
| + | <center><math> \Pi_3 = \frac{\mathbf{X}_3(\omega)}{-\omega^2(A_{33} + M) + i\omega B_{33} +C_{33} } </math></center> | ||
| + | |||
| + | Resonance: | ||
| + | |||
| + | <center><math> \omega^2 = \frac{C_{33}}{M+A_{33}} = \frac{\rho g A \omega}{M + A_{33} (\omega)} </math></center> | ||
| + | |||
| + | In principle the above equation is nonlinear for <math>\omega\,</math>. Will be approximated below | ||
| + | |||
| + | At resonance: | ||
| + | <center><math> \Pi_3 = \frac{\mathbf{X}_3(\omega^*)}{i\omega^* B_{33}(\omega^*)} \,</math></center> | ||
| + | |||
| + | Invoking the relation between the damping coefficient and the exicting force in 3D: | ||
| + | |||
| + | <center><math> \frac{\left| \Pi_3 \right|}{A} = \frac{\left| \mathbf{X}_3(\omega) \right|}{\omega \frac{K}{4\rho g V_g} \left| \mathbf{X}_3 \right|^2}, \quad V_g=\frac{g}{2\omega} </math></center> | ||
| + | |||
| + | <center><math> =\frac{2\rho g}{\omega^3 \left|\mathbf{X}_3(\omega)\right|}, \quad \mbox{at resonance} </math></center> | ||
| + | |||
| + | This counter-intuitive result shows that for a body undergoing a pure Heave oscillation, the modulus of the Heave response at resonance is inversely proportional to the modulus of the Heave exciting force. | ||
| + | |||
| + | Viscous effects not discussed here may affect Heave response at resonance | ||
| + | |||
| + | The behavior of the Sway response can be found in an analagous manner, | ||
| + | |||
| + | |||
| + | ----- | ||
| + | |||
| + | This article is based on the MIT open course notes and the original articles can be found | ||
| + | [http://ocw.mit.edu/NR/rdonlyres/Mechanical-Engineering/2-24Spring-2002/666E84F4-5679-47FD-BD7B-9D39877DE5A1/0/lecture9.pdf here] and | ||
| + | [http://ocw.mit.edu/NR/rdonlyres/Mechanical-Engineering/2-24Spring-2002/C5323823-0180-45EA-B165-15856948A0A2/0/lecture10.pdf here] | ||
Latest revision as of 12:58, 26 April 2011
| Wave and Wave Body Interactions | |
|---|---|
| Current Chapter | Linear Wave-Body Interaction |
| Next Chapter | Long Wavelength Approximations |
| Previous Chapter | Ship Kelvin Wake |
We consider a Linear Plane Progressive Regular Wave in the Frequency Domain interacting with a floating body in two dimensions (the main concepts survive almost with no change in the more practical three-dimensional problem).
Introduction
We derive here the equations of motion for a body in Linear Plane Progressive Regular Waves in the frequency domain in two dimensions. We begin with the equations in the time domian. The simplest problems is Waves reflecting off a vertical wall
Equations for a Floating Body in the Time Domain
We begin with the equations for a floating two-dimensional body in the time domain.
The equations of motion in the time domain are Laplace's equation through out the fluid
At the bottom surface we have no flow
At the free surface we have the kinematic condition
and the dynamic condition (the linearized Bernoulli equation)
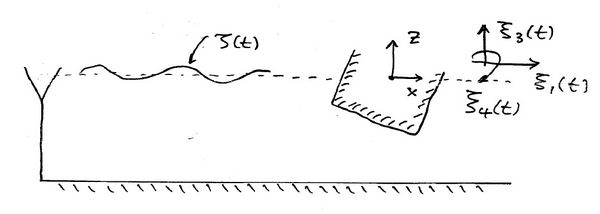
The body boundary condition for a floating body is given in terms of the 3 rigid body motions, namely surge, heave and pitch which are indexed as [math]\displaystyle{ \nu=1,3,5 }[/math] in order to be consistent with the three-dimensional problem. We have a kinematic condition
where [math]\displaystyle{ \xi_{\nu} }[/math] is the motion of the [math]\displaystyle{ \mu }[/math]th mode and [math]\displaystyle{ \mathbf{n}_{\nu} }[/math] is the normal associated with this mode. Note that we define all normal derivatives to point out of the fluid. The dynamic condition is the equation of motion for the structure:
In this equation, [math]\displaystyle{ M_{\mu\nu} }[/math] are the elements of the mass matrix
for the structure and [math]\displaystyle{ c_{\mu\nu} }[/math] are the elements of the buoyancy matrix
The terms [math]\displaystyle{ I^b_{11} }[/math], [math]\displaystyle{ I^b_{33} }[/math] are the moments of inertia of the body about the [math]\displaystyle{ x }[/math] and [math]\displaystyle{ z }[/math] axes and the terms [math]\displaystyle{ I_1^{A} }[/math], [math]\displaystyle{ I^{A}_{11} }[/math] are the first and second moments of the waterplane (the waterplane area is denoted [math]\displaystyle{ W }[/math]) about the [math]\displaystyle{ x }[/math]-axis (see Chapter 7, Mei 1983). In addition, [math]\displaystyle{ (x^c,z^c) }[/math] and [math]\displaystyle{ (X^R,Z^R) }[/math] are the positions of the centre of mass and centre of rotation of the body and [math]\displaystyle{ I^{V}_{3} }[/math] is [math]\displaystyle{ z }[/math]-component centre of buoyancy of the structure. Thus, the coupled equations of motion for a floating structure have been derived. (N.B. if is assumed that the centre of rotation and the centre of mass of the structure coincide, i.e. if it is assumed that the body is semi-submerged, the mass and buoyancy matrices become diagonal). Any wave incidence is assumed to be propagating in the positive [math]\displaystyle{ x }[/math] direction.) The scattering and radiation problems are simpler than the coupled problem because the motion of the the structure is then prescribed.
More details can be found in Time-Dependent Linear Water Waves
Equations for a Floating Body in the Frequency Domain
The dynamic condition is the equation of motion for the structure in the frequency domain can be found from the time domain equations and we introduce the following notation
This give us
(note that the last expression can be obtained from combining the expressions:
where [math]\displaystyle{ \alpha = \omega^2/g \, }[/math])
The equations of motion for [math]\displaystyle{ \zeta_\nu\, }[/math] follow from Newton's law applied to each mode in two dimensions. The same principles apply with very minor changes in three dimensions. We use the standard numbering of the modes of motion.
Equations for a Fixed Body in Frequency Domain
The equations for a fixed body are
(note that the last expression can be obtained from combining the expressions:
where [math]\displaystyle{ \alpha = \omega^2/g \, }[/math]) The body boundary condition for a rigid body is just
plus the radiation conditions.
We decompose the potential as [math]\displaystyle{ \phi = \phi^{\mathrm{I}} + \phi^{\mathrm{D}} \,, }[/math] where [math]\displaystyle{ \phi^{\mathrm{I}} }[/math] is the incident potential and [math]\displaystyle{ \phi^{\mathrm{D}} }[/math] is the diffracted potential. The boundary condition for the diffracted potential is
plus
Code to calculate the solution (using a slighly modified method) can be found in Boundary Element Method for a Fixed Body in Finite Depth
Equations for the Radiation Potential in Frequency Domain
We decompose the body motion into the rigid body modes of motion. Associated with each of these modes is a potential which must be solved for. The equations for the radiation potential in the frequency domain are
(note that the last expression can be obtained from combining the expressions:
where [math]\displaystyle{ \alpha = \omega^2/g \, }[/math]) The body boundary condition for a radiation mode [math]\displaystyle{ m }[/math] is just
where [math]\displaystyle{ \mathbf{n}_{\nu} }[/math] is the normal derivative of the [math]\displaystyle{ \nu }[/math] mode on the body surface directed out of the fluid.
In two-dimensions the Sommerfeld Radiation Condition is
Code to calculate the radiation potential can be found in Boundary Element Method for the Radiation Potential in Finite Depth
We denote the solution for each of the radiation potentials by [math]\displaystyle{ \phi_\nu^{\mathrm{R}} }[/math] and the total potential is written as
Final System of Equations
We substitute the expansion for the potential into the equations in the frequency domain and we obtain
We define the added mass matrix by
and the damping matrix by
and the forcing vector by
Then the equations can be expressed as follows.
where [math]\displaystyle{ \mathbf{M} }[/math] is the mass matrix, [math]\displaystyle{ \mathbf{A} }[/math] is the added mass matrix, [math]\displaystyle{ \mathbf{B} }[/math] is the damping matrix, [math]\displaystyle{ \mathbf{C} }[/math] is the hydrostatic matrix, [math]\displaystyle{ \vec{\zeta} }[/math] is the vector of body displacements and [math]\displaystyle{ \mathbf{f} }[/math] is the force.
The extension of these equations to six degrees of freedom is straightforward. However before discussing the general case we will study specific properties of the two dimensional problem for the sake of clarity.
Symmetric body
For a body which is Symmetric in Two Dimensions the Heave is decoupled from Surge and Roll. In other words the Surge and Roll motions do not influence Heave and vice versa.
Matlab Code
- A program to solve for pitch and heave and only for two geometries can be found here rigid_body_motion.m
- a program to calculate the solution for a specific geometry (with plot as output as shown) can be found here wave_bem_example_floating.m
Additional code
This program requires
- A program to calculate the geometery circlebody_twod.m
- A program to solve for a fixed body fixed_body_twod.m
- A program to solve the radiation problem for a floating body can be found here forced_body_twod.m
- dispersion_free_surface.m
- A program to calculate the matrices [math]\displaystyle{ G }[/math] and [math]\displaystyle{ G_{n} }[/math] bem_constant_panel.m
Symmetry-reciprocity relations
It will be shown that
Along the same lines it will be shown that the exciting force [math]\displaystyle{ \mathbf{X}_j\, }[/math] can be expressed in terms of [math]\displaystyle{ \psi_j\, }[/math] circumventing the solution for the diffraction potential. The core result needed for the proof of the above properties is Green's second identity
where [math]\displaystyle{ \nabla^2 \psi_i=0 }[/math].
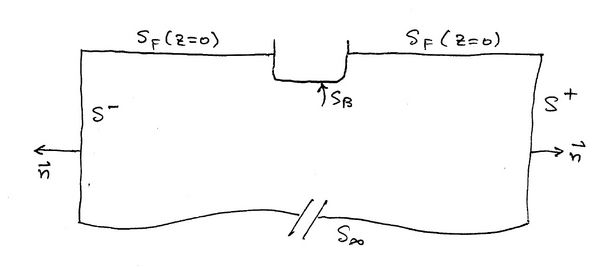
In the surface wave-body problem define the closed surfaces as shown in figure on the right. Let [math]\displaystyle{ \phi_j\, }[/math] be rediation or diffraction potentials. Over the boundaries [math]\displaystyle{ S^\pm\, }[/math] we have:
On [math]\displaystyle{ S_F: \qquad \frac{\partial\phi_j}{\partial z} = K\phi_j, \qquad \frac{\partial \Phi_j}{\partial n} = \frac{\partial \phi_j}{\partial z} }[/math]
On [math]\displaystyle{ S_\infty: \qquad \left| \phi_j \right|, \quad \left| \nabla \phi_j \right| \to 0 }[/math].
Applying Green's identity to any pair of the radiation potentials [math]\displaystyle{ \psi_i, \psi_j \, }[/math]:
It follows that:
or
Haskind relations of exciting forces
where the radiation velocity potential [math]\displaystyle{ \phi_i \, }[/math] is known to satisfy:
and
Both [math]\displaystyle{ \phi_i\, }[/math] and [math]\displaystyle{ \phi_7\, }[/math] satisfy the condition of outgoing waves at infinity. By virtue of Green's second identity
The Haskind expression for the exciting force follows:
The symmetry of the [math]\displaystyle{ A_{ij}(\omega), B_{ij}(\omega) \, }[/math] matrices applies in 2D and 3D. The application of Green's Theorem in 3D is very similar using the far-field representation for the potential [math]\displaystyle{ \phi_j\, }[/math]
where [math]\displaystyle{ R \, }[/math] is a radius from the body out to infinity and the [math]\displaystyle{ R^{-\frac{1}{2}} \, }[/math] decay arises from the energy conservation principle. Details of the 3D proof may be found in Mei 1983 and Wehausen and Laitone 1960
The use of the Haskind relations for the exciting forces does not require the solution of the diffraction problem. This is convenient and often more accurate.
The Haskind relations take other forms which will not be presented here but are detailed in Wehausen and Laitone 1960. The ones that are used in practice relate the exciting forces to the damping coefficients.
These take the form:
2D: [math]\displaystyle{ B_{ii} = \frac{\left| \mathbf{X}_i \right|^2}{2\rho g V_g}, \quad V_g = \frac{g}{2\omega}, }[/math] Deep water
3D: [math]\displaystyle{ B_{33} = \frac{K}{4\rho g V_g} \left| \mathbf{X}_3 \right|^2 \, }[/math] --- Heave
(Axisymmetric bodies) [math]\displaystyle{ B_{22} = \frac{K}{8\rho g V_g} \left| \mathbf{X}_2 \right|^2 \, }[/math] --- Sway
So knowledge of [math]\displaystyle{ \mathbf{X}_i(\omega)\, }[/math] allows the direct evaluation of the diagonal damping coefficients. These expressions are useful in deriving theoretical results in wave-body interactions to be discussed later.
The two-dimensional theory of wave-body interactions in the frequency domain extends to three dimencions very directly with little difficulty.
The statement of the 6 d.o.f. seakeeping problem is:
where
At zero speed the definitions of the added-mass, damping matrices and exciting forces are identical to those in two dimensions.
The boundary value problems satisfied by the radiation potentials [math]\displaystyle{ \phi_j, \ j=1,\cdots,6 \, }[/math] and the diffraction potential [math]\displaystyle{ \phi_7 \, }[/math] are as follows:
Free-surface condition:
Body-boundary conditions:
At large distances from the body the velocity potentials satisfy the radiation condition:
with
This radiation condition is essential for the formulation and solution of the boundary value problems for [math]\displaystyle{ \phi_j\, }[/math] using panel methods which are the standard solution technique at zero and forward speed.
Qualitative behaviour of the forces, coefficients and motions of floating bodies
The 2D Heave added mass is singular at low frequencies. It is finite in 3D
The 2D Heave damping coefficient is decaying to zero linearly in 2D and superlinearly in 3D. A two-dimensional section is a better wavemaker than a three-dimensional one
A 2D section oscillating in Sway is less effective a wavemaker at low frequencies than the same section oscillating in Heave
The zero-frequency limit of the Sway added mass is finite and similar to the infinite frequency limit of the Heave added mass.
In long waves the Heave exciting force tends to the Heave restoring coefficient times the ambient wave amplitude the free surface behaves like a flat surface moving up and down.
In long waves the Sway exciting force tends to zero. Proof will follow
In short waves all forces tend to zero.
Pitch exciting moment (same applies to Roll) tends to zero. Long waves have a small slope which is proportional to [math]\displaystyle{ KA }[/math], where [math]\displaystyle{ K\, }[/math] is the wave number and [math]\displaystyle{ A\, }[/math] is the wave amplitude.
Prove that to leading order for [math]\displaystyle{ KA\to 0 \, }[/math]:
where [math]\displaystyle{ C_{55}\, }[/math] is the Pitch ([math]\displaystyle{ C_{44} \, }[/math] for Roll) hydrostatic restoring coefficient. [NB: very long waves look like a flat surface inclined at [math]\displaystyle{ KA\, }[/math] ].
Body motions in regular waves
Heave:
Resonance:
In principle the above equation is nonlinear for [math]\displaystyle{ \omega\, }[/math]. Will be approximated below
At resonance:
Invoking the relation between the damping coefficient and the exicting force in 3D:
This counter-intuitive result shows that for a body undergoing a pure Heave oscillation, the modulus of the Heave response at resonance is inversely proportional to the modulus of the Heave exciting force.
Viscous effects not discussed here may affect Heave response at resonance
The behavior of the Sway response can be found in an analagous manner,
This article is based on the MIT open course notes and the original articles can be found here and here