Green Function Method for a Finite Dock

This is an incomplete page

Introduction

The problem of a two-dimensional finite dock is solved using a green function. The same problem is solved using eigenfunction matching in Eigenfunction Matching for a Finite Dock.

Equations for a Dock in the Frequency Domain

Wave scattering by a finite dock

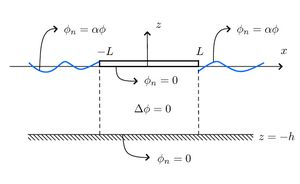
We consider here the Frequency Domain Problem for a finite dock which occupies the region [math]\displaystyle{ -L\lt x\lt L }[/math] (we assume [math]\displaystyle{ e^{i\omega t} }[/math] time dependence). The water is assumed to have constant finite depth [math]\displaystyle{ h }[/math] and the [math]\displaystyle{ z }[/math]-direction points vertically upward with the water surface at [math]\displaystyle{ z=0 }[/math] and the sea floor at [math]\displaystyle{ z=-h }[/math]. The boundary value problem can therefore be expressed as

[math]\displaystyle{ \Delta\phi=0, \,\, -h\lt z\lt 0, }[/math]

[math]\displaystyle{ \phi_{z}=0, \,\, z=-h, }[/math]

[math]\displaystyle{ \partial_z\phi=\alpha\phi, \,\, z=0,\,x \lt -L, {\rm or} \, x\gt L }[/math]

[math]\displaystyle{ \partial_z\phi=0, \,\, z=0,\,-L\lt x\lt L, }[/math]

We must also apply the Sommerfeld Radiation Condition as [math]\displaystyle{ |x|\rightarrow\infty }[/math]. This essentially implies that the only wave at infinity is propagating away and at negative infinity there is a unit incident wave and a wave propagating away.

Equation in Terms of the Modes of the Plate

Under these assumptions, the equations become

[math]\displaystyle{ \Delta\phi =0,\,\,-h\lt z\lt 0, }[/math] [math]\displaystyle{ \partial_{z}\phi =0,\,\,z=-h, }[/math] [math]\displaystyle{ \alpha\phi =\partial_{z}\phi,\,\,x\notin(-L,L),\ \ z=0, }[/math] [math]\displaystyle{ i\omega\sum_{n=0}^{\infty}\zeta_{n}X_{n} =\partial_{z}\phi,\,\,x\in (-L,L),\,\, z=0, }[/math] [math]\displaystyle{ \sum_{n=0}^{\infty}\zeta_{n}\left( 1+\beta\lambda_{n}^{4}\right) X_{n}-\alpha\gamma\sum_{n=0}^{\infty}\zeta_{n}X_{n} = -i\omega \phi,\,\,x\in(-L,L),\,\, z=0. }[/math]

We solve for the potential (and displacement) as the sum of the diffracted and radiation potentials in the standard way, as for a rigid body.

[math]\displaystyle{ \phi=\phi^{\mathrm{D}}+\phi^{\mathrm{R}} ,\, }[/math]

We begin with the diffraction potential [math]\displaystyle{ \phi^{\mathrm{D}} }[/math] which satisfies the following equations

[math]\displaystyle{ \Delta\phi^{\mathrm{D}} =0,\,\,-h\lt z\lt 0, }[/math] [math]\displaystyle{ \partial_{z}\phi^{\mathrm{D}} =0,\,\,z=-h, }[/math] [math]\displaystyle{ \partial_{z}\phi^{\mathrm{D}} =\alpha \phi^{\mathrm{D}},\,\,x\notin(-L,L),\,\, z=0, }[/math] [math]\displaystyle{ \partial_{z}\phi^{\mathrm{D}} =0,\,\,x\in(-L,L),\,\,z=0. }[/math]

Furthermore, [math]\displaystyle{ \phi^{\mathrm{D}} }[/math] satisfies the Sommerfeld Radiation Condition

[math]\displaystyle{ \frac{\partial}{\partial x} \left(\phi^{\mathrm{D}}-\phi^{\rm I} \right) \pm ik\left( \phi^{\mathrm{D}}-\phi^{\rm I}\right) = 0 ,\,\,\mathrm{as} \,\,x\rightarrow\pm\infty, }[/math]

where [math]\displaystyle{ k ,\, }[/math] is the wavenumber, which is the positive real solution of the Dispersion Relation for a Free Surface

[math]\displaystyle{ k\tanh(kh)=\omega^{2} \, }[/math]

and [math]\displaystyle{ \phi^{\rm I} }[/math] is the incident wave given by

[math]\displaystyle{ \phi^{\rm I} = \frac{\cosh(k(z+h))}{\cosh(kh)} e^{-i kx} \, }[/math]

(which has unit amplitude in potential) and is travelling towards positive infinity.

As the plate is floating on the surface, we can denote it as follows:

[math]\displaystyle{ \phi^{\rm I}|_{z=0} = e^{-i kx} \, }[/math]

We now consider the scattered potentials [math]\displaystyle{ \phi^{\mathrm{S}} }[/math]. The relationship between scattered potentials, diffracted potentials and the incident wave are as follows:

[math]\displaystyle{ \phi^{\mathrm{D}}=\phi^{\mathrm{I}}+\phi^{\mathrm{S}} \, }[/math]

from this, we can construct the following conditions:

[math]\displaystyle{ \Delta\phi^{\mathrm{S}} =0,\,\,-h\lt z\lt 0, }[/math] [math]\displaystyle{ \partial_{z}\phi^{\mathrm{S}} =0,\,\,z=-h, }[/math] [math]\displaystyle{ \partial_{z}\phi^{\mathrm{S}} =\alpha\phi^{\mathrm{S}},\,\,x\notin(-L,L),\, \, z=0 }[/math] [math]\displaystyle{ \partial_{z}\phi^{\mathrm{S}} = -\partial_{z}\phi^{\mathrm{I}},\,\,x\in(-L,L),\,\,z=0. }[/math]

We now consider the radiation potentials [math]\displaystyle{ \phi^{\mathrm{R}} }[/math]. We can express the radiation potential as:

[math]\displaystyle{ \phi^{\mathrm{R}}=\sum_{n=0}^{\infty}\zeta_n \phi_n^{\mathrm{R}} }[/math]

which satisfy the following equations

[math]\displaystyle{ \Delta\phi_n^{\mathrm{R}} =0,\,\,-h\lt z\lt 0, }[/math] [math]\displaystyle{ \partial_{z}\phi_n^{\mathrm{R}} =0,\,\,z=-h, }[/math] [math]\displaystyle{ \partial_{z}\phi_n^{\mathrm{R}} =\alpha\phi_n^{\mathrm{R}},\,\,x\notin(-L,L),\, \, z=0 }[/math] [math]\displaystyle{ \partial_{z}\phi_n^{\mathrm{R}} = i\omega X_{n},\,\,x\in(-L,L),\,\,z=0. }[/math]

The radiation condition for the radiation potential is

[math]\displaystyle{ \frac{\partial\phi_n^{\mathrm{R}}}{\partial x}\pm ik\phi_n^{\mathrm{R}}=0,\,\,\mathrm{as} \,\,x\rightarrow\pm\infty. }[/math]

Therefore we find the potential as

[math]\displaystyle{ \phi=\phi^{\mathrm{D}} +\sum_{n=0}^{\infty}\zeta_{n}\phi_n^{\mathrm{R}}, }[/math]

so that

[math]\displaystyle{ \sum_{n=0}^{\infty}\left( 1+\beta\lambda_{n}^{4} - \alpha\gamma\right) \zeta_{n}X_{n}=-i\omega \left( \phi^{\mathrm{D}}+\sum_{n=0}^{\infty}\zeta_{n}\phi_n^{\mathrm{R}} \right). }[/math]

If we multiply by [math]\displaystyle{ X_m }[/math] and take an inner product over the plate we obtain

[math]\displaystyle{ \left( 1+\beta\lambda_{n}^{4} - \alpha\gamma\right) \zeta_{n}=-i\omega \int_{-L}^{L}\phi^{\mathrm{D}} X_{n}\mathrm{d}x + \sum_{m=0}^{\infty}\left(\omega^2 a_{mn}(\omega) - i\omega b_{mn}(\omega)\right) \zeta_{m}, }[/math]

where the functions [math]\displaystyle{ a_{mn}(\omega) }[/math] and [math]\displaystyle{ b_{mn}(\omega) }[/math] are given by

[math]\displaystyle{ \omega^2 a_{mn}(\omega) -i\omega b_{mn}(\omega) = - i\omega\int_{-L}^{L}\phi_m^{\mathrm{R}}X_{n}\mathrm{d}x, }[/math]

and they are referred to as the added mass and damping coefficients (see Added-Mass, Damping Coefficients And Exciting Forces for the equivalent definition for a rigid body). respectively. This equation is solved by truncating the number of modes.

Solution for the Radiation and Diffracted Potential

We use the Free-Surface Green Function for two-dimensional waves, with singularity at the water surface since we are only interested in its value at [math]\displaystyle{ z=0. }[/math] Using this we can transform the system of equations to

[math]\displaystyle{ \phi^{\mathrm{D}}(x) = \phi^{\mathrm{I}}(x) + \int_{-L}^{L}G(x,\xi) \alpha\phi^{\mathrm{S}}(\xi) \mathrm{d} \xi }[/math]

and

[math]\displaystyle{ \phi_n^{\mathrm{R}}(x) = \int_{-L}^{L}G(x,\xi) \left( \alpha\phi_n^{\mathrm{R}}(\xi) - i\omega X_n(\xi) \right)\mathrm{d} \xi }[/math]

Details about this method can be found in Integral Equation for the Finite Depth Green Function at Surface.

Reflection and Transmission Coefficients

The Reflection and Transmission Coefficients represent the ratio of the amplitude of the reflected or transmitted wave to the amplitude of the incident wave. They hold the property that [math]\displaystyle{ |R|^2+|T|^2=1\, }[/math] (and may often contain an imaginery element).

A diagram depicting the area [math]\displaystyle{ \Omega\, }[/math] which is bounded by the rectangle [math]\displaystyle{ \partial \Omega \, }[/math]. The rectangle [math]\displaystyle{ \partial \Omega \, }[/math] is bounded by [math]\displaystyle{ -h \leq z \leq 0 \, }[/math] and [math]\displaystyle{ -\infty \leq x \leq \infty \, }[/math] or [math]\displaystyle{ -N \leq x \leq N\, }[/math]

We can calculate the Reflection and Transmission coefficients as follows: Applying Green's theorem to [math]\displaystyle{ \phi\, }[/math] and [math]\displaystyle{ \phi^{\mathrm{I}}\, }[/math] gives:

[math]\displaystyle{ 0 = \iint_{\Omega}(\phi\nabla^2\phi^{\mathrm{I}} - \phi^{\mathrm{I}}\nabla^2\phi)\mathrm{d}x\mathrm{d}z = \int_{\partial\Omega}(\phi\frac{\partial\phi^{\rm I}}{\partial n} - \phi^{\rm I}\frac{\partial\phi}{\partial n})\mathrm{d}l, }[/math] [math]\displaystyle{ = \phi_0(0) \int_{-L}^{L} e^{k_0 x} \left(\alpha \phi(x) - \partial_n \phi(x)\right)\mathrm{d}x - 2k_0 R \int_{-h}^{0} \left(\phi_0(z)\right)^2 \mathrm{d}z. }[/math]

<br\>

where [math]\displaystyle{ k_0 \, }[/math] is the first imaginery root of the dispersion equation and the incident wave is of the form: [math]\displaystyle{ \phi^I=\phi_0(z)e^{-ikx} \, }[/math]<br\><br\> Therefore, in the case of a floating plate (where z=0):

[math]\displaystyle{ R = \frac{\int_{-L}^{L} e^{k_0 x} \left(\alpha \phi(x) - \partial_n \phi(x)\right)\mathrm{d}x } {2 k_0 \int_{-h}^{0} \left(\phi_0(z)\right)^2 \mathrm{d}z}. }[/math]

and using a wave incident from the right we obtain

[math]\displaystyle{ 1 + T = \frac{\int_{-L}^{L} e^{-k_0 x} \left(\alpha \phi(x) - \partial_n \phi(x)\right)\mathrm{d}x } {2 k_0 \int_{-h}^{0} \left(\phi_0(z)\right)^2 \mathrm{d}z}. }[/math]

Matlab Code

A program to calculate the solution in elastic modes can be found here A program to calculate the solution in elastic modes can be found here

elastic_plate_modes.m

Additional code

This program requires

• matrix_G_surface.m
• two_d_finite_depth_Green_surface.m
• dispersion_free_surface.m
• beam_ev.m
• beam_em.m

Additional code

This program requires

• matrix_G_surface.m
• two_d_finite_depth_Green_surface.m
• dispersion_free_surface.m
• beam_ev.m
• beam_em.m

Alternative Solution Method using Green Functions for a Uniform Plate

We can also solve the equation by a closely related method which was given in Meylan and Squire 1994. We can transform the equations to

[math]\displaystyle{ \phi(x) = \phi^{\rm I}(x) + \int_{-L}^{L}G(x,\xi) \left( \alpha\phi(\xi) - \partial_z\phi(\xi) \right)\mathrm{d} \xi }[/math]

Expanding as before

[math]\displaystyle{ \partial_z \phi = i\omega \sum \xi_n X_n }[/math]

we obtain

[math]\displaystyle{ -i\omega \phi = \sum \left(\beta\lambda_n^4 - \gamma\alpha + 1\right)\xi_n X_n }[/math]

This leads to the following equation

[math]\displaystyle{ \partial_z\phi(x) = \frac{1}{\alpha} \int_{-L}^{L} \frac{X_n(x)X_n(\xi)}{\beta\lambda_n^4 - \gamma\alpha + 1} \phi(\xi)\mathrm{d}\xi }[/math]

or

[math]\displaystyle{ \partial_z\phi(x) = \frac{1}{\alpha} \int_{-L}^{L} g(x,\xi) \phi(\xi)\mathrm{d}\xi }[/math]

where

[math]\displaystyle{ g(x,\xi) = \frac{X_n(x)X_n(\xi)}{\beta\lambda_n^4 - \gamma\alpha + 1} }[/math]

which is the Green function for the plate.