Linear Wave-Body Interaction

Introduction

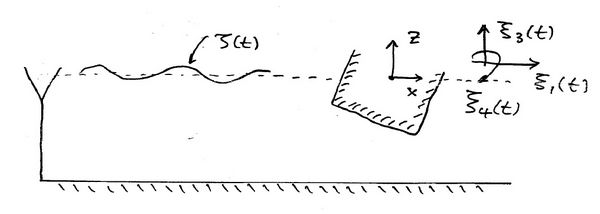
We derive here the equations of motion for a floating body in Linear Plane Progressive Regular Waves in two dimensions.

Linear wave-body interactions

Rigid body motions

Consider a Linear Plane Progressive Regular Wave interacting with a floating body in two dimensions (the main concepts survive almost with no change in the more practical three-dimensional problem). We begin by defining the following,

[math]\displaystyle{ \zeta(t): \quad \mbox{ambient wave elevation. Regular or random with definitions to be given below}. \, }[/math] [math]\displaystyle{ \xi_1(t): \quad \mbox{Body surge displacement} \, }[/math] [math]\displaystyle{ \xi_3(t): \quad \mbox{Body heave displacement} \, }[/math] [math]\displaystyle{ \xi_4(t): \quad \mbox{Body roll displacement} \, }[/math]

where the surge, heave and roll and the three rigid body motions which are possible in two dimensions.

Linear theory

We assume that we can apply linear theory to the motions, which are an extension of the linear equations for a free-surface. We assume that

[math]\displaystyle{ \left| \frac{\partial\zeta}{\partial x} \right| = O(\varepsilon) \ll 1 \, }[/math]

This is an assumption of small wave steepness which is a reasonable assumption for gravity waves in most cases, except when waves are near breaking conditions. Further more we assume

[math]\displaystyle{ \left| \frac{\xi_1}{A} \right| = O(\varepsilon) \ll 1 \, }[/math] [math]\displaystyle{ \left| \frac{\xi_3}{A} \right| = O(\varepsilon) \ll 1 \, }[/math] [math]\displaystyle{ \left| \xi_4 \right| = O(\varepsilon) \ll 1 \, }[/math]

These assumptions are valid in most cases and most bodies of practical interest, unless the vessel response at resonance is highly tuned or lightly damped. This is often the case for roll when a small amplitude wave interacts with a vessel weakly damped in roll.

Linear Systems theory

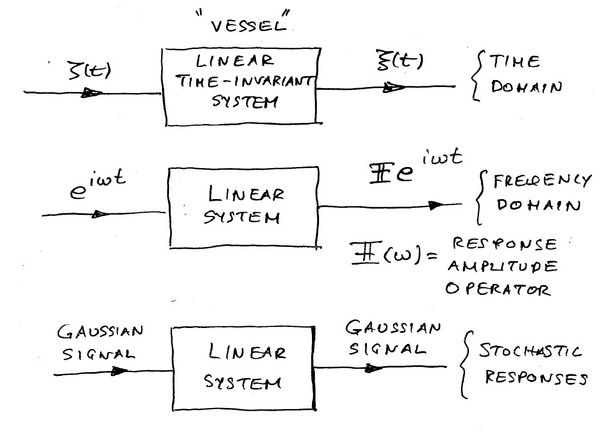
Linear systems theory

The vessel dynamic responses in waves may be modelled according to linear system theory. By virtue of linearity, a random seastate may be represented as the linear super position of Linear Plane Progressive Regular Waves (see Waves and the Concept of a Wave Spectrum)

[math]\displaystyle{ \zeta(x,t) = \sum_j A_j \cos ( K_j x - \omega_j t + \epsilon_j ) \, }[/math]

where in deep water: [math]\displaystyle{ K_j = \frac{\omega_j^2}{g} \, }[/math]. Note that the sum here can be replace by an integral in many formulations. According to the theory of St. Denis and Pierson, the phases [math]\displaystyle{ \epsilon\, }[/math], are random and uniformly distributed between [math]\displaystyle{ ( - \pi, \pi ] \, }[/math]. For now we assume them known constants:

At [math]\displaystyle{ X=0\, }[/math]:

[math]\displaystyle{ \zeta(t) = \sum_j A_j \cos ( \omega_j t - \epsilon_j ) \, }[/math] [math]\displaystyle{ = \mathfrak{Re} \sum_j A_j e^{i\omega_j t - i \epsilon_j} }[/math]

The corresponding vessel responses follow from linearity in the form:

[math]\displaystyle{ \xi_K (t) = \mathfrak{Re} \sum_j \Pi_K (\omega_j) e^{i\omega_j t - i\epsilon_j}, \qquad K = 1, 3, 4 }[/math]

Where [math]\displaystyle{ \Pi_K (\omega) \, }[/math] is the complex RAO (Response Amplitude Operator) for mode [math]\displaystyle{ K\, }[/math]. It is the object of linear seakeeping theory to derive equations for [math]\displaystyle{ \Pi\omega)\, }[/math] the frequency domain. The treatment in the stochastic case is then a simple exercise in linear systems.

Calculation of the RAO

The equations of motion for [math]\displaystyle{ \xi_K(t)\, }[/math] follow from Newton's law applied to each mode in two dimensions. The same principles apply with very minor changes in three dimensions

We begin by considering the equation in surge.

[math]\displaystyle{ \mathbf{M} \frac{d^2\xi_1}{dt^2} = F_{1\omega} ( \xi_1, \dot\xi_1, \ddot\xi_1, t) }[/math]

where [math]\displaystyle{ \frac{d\xi_1}{dt} = \dot\xi_1 \, }[/math] and [math]\displaystyle{ F_{1\omega} \, }[/math] is the force on the body due to the fluid pressures, by virtue of linearity, [math]\displaystyle{ F_{1\omega} \, }[/math] will be assumed to be a linear functional of [math]\displaystyle{ \xi_1, \dot\xi_1, \ddot\xi_1 \, }[/math]. Memory effects exist when surface waves are generated on the free surface, so [math]\displaystyle{ F_{1\omega} \, }[/math] depends in principle on the entire history of the vessel displacement. We adopt here the frequency domain formulation where the vessel motion has been going on over an infinite time interval, [math]\displaystyle{ (-\infty, t)\, }[/math] with [math]\displaystyle{ e^{i\omega t}\, }[/math] dependence.

We will therefore set:

[math]\displaystyle{ \xi_K(t) = \mathfrak{Re} \left\{ \Pi_K e^{i\omega t} \right\}, \qquad K=1,3,4 }[/math]

In this case we can linearize the water induced force on the body as follows:

[math]\displaystyle{ F_{1\omega}(t) = X_1(t) - A_{11} \ddot \xi_1 - A_{13} \ddot \xi_3 - A_{14} \ddot \xi_4 }[/math] [math]\displaystyle{ - B_{11} \dot \xi_1 - B_{13} \dot \xi_3 - B_{14} \dot \xi_4 }[/math] [math]\displaystyle{ - C_{11} \xi_1 - C_{13} \xi_3 - C_{14} \xi_4 \, }[/math] [math]\displaystyle{ = X_1(t) - \sum_j \left[ A_{1j} \ddot \xi_j + B_{1j} \dot \xi_j + C_{1j} \xi_j \right] }[/math]

The same expansion applies for other modes, namely Heave ([math]\displaystyle{ K = 3 \, }[/math]) and Roll ([math]\displaystyle{ K=4 \, }[/math]). In sum:

[math]\displaystyle{ F_{K\omega} (t) = X_K - \sum_j \left[ A_{Kj} \ddot \xi_j + B_{Kj} \dot \xi_j + C_{Kj} \xi_j \right], \qquad K = 1,3,4 }[/math]

• The added-mass matrix [math]\displaystyle{ A_{Kj} \, }[/math] represents the added inertia due to the acceleration of the body in water with acceleration [math]\displaystyle{ \ddot\xi_j\, }[/math].

• The damping matrix [math]\displaystyle{ B_{Kj}\, }[/math] governs the energy dissipation into the fluid domain in the form of surface waves.

• The hydrostatic restoring matrix [math]\displaystyle{ C_{Kj} \, }[/math] represents the system stifness due to the hydrostatic restoring forces and moments.

For harmonic motions, the matrices [math]\displaystyle{ A_{Kj} \, }[/math] and [math]\displaystyle{ B_{Kj} \, }[/math] are functions of [math]\displaystyle{ \omega\, }[/math], so we write [math]\displaystyle{ A_{Kj} (\omega), \ B_{Kj} (\omega)\, }[/math]. This functional form will be discussed below. The hydrostatic matrix [math]\displaystyle{ C_{Kj} \, }[/math] is independent of [math]\displaystyle{ \omega\, }[/math] and many of its elements are identically equal to zero. Collecting terms in the left-hand side and denoting by [math]\displaystyle{ M_{Kj}\, }[/math] the body inertia matrix:

Surge

[math]\displaystyle{ \sum_j \left[ -\omega^2 \left( M_{1j} + A_{1j} \right) + i\omega B_{1j} + C_{1j} \right] \Pi_j = \mathbf{X}_1 (\omega), \quad j=1,3,4 }[/math]

Heave

[math]\displaystyle{ \sum_j \left[ -\omega^2 \left( M_{3j} + A_{3j} \right) + i\omega B_{3j} + C_{3j} \right] \Pi_j = \mathbf{X}_3 (\omega), \quad j=1,3,4 }[/math]

Roll

[math]\displaystyle{ \sum_j \left[ -\omega^2 \left( I_G + A_{4j} \right) + i\omega B_{4j} + C_{4j} \right] \Pi_j = \mathbf{X}_4 (\omega) }[/math]

The extension of these equations to six degrees of freedom is straightforward. However before discussing the general case we will study specific properties of the 2D Problem for the sake of clarity.

Symmetric body

Consider a body symmetric about the [math]\displaystyle{ X = 0\, }[/math] axis.

Exercises

For a body symmetric port/starboard:

• Verify that Heave is decoupled from Surge and Roll. In other words the Surge and Roll motions do not influence Heave and vice versa:

[math]\displaystyle{ \left[ -\omega^2 \left( M + A_{33} \right) + i\omega B_{33} + C_{33} \right] \Pi_3 = A }[/math]

• The only nonzero hydrostatic coefficients are [math]\displaystyle{ C_{33} \, }[/math] and [math]\displaystyle{ C_{44} \, }[/math]. Verify that this is the case even for non-symmetric sections.

• Surge and Roll are coupled for symmetric and non-symmetric bodies. The coupled equation of motion becomes:

Surge-Roll

[math]\displaystyle{ \sum_{j=1,4} \left[ -\omega^2 \left( M_{ij} + A_{ij} \right) + i\omega B_{ij} + C_{ij} \right] \Pi_j = \mathbf{X}_i, \quad i,j = 1,4 }[/math]

• When Newton's law is expressed about the center of gravity:

[math]\displaystyle{ M_{14} = M_{41} = 0, \ M_{11} = M, \ M_{44} = I_G }[/math]

where [math]\displaystyle{ I_G\, }[/math] is the body moment of inertia about the center of gravity. If the equations are to be expressed about the origin of the coordinate system, then the formulation must start with respect to [math]\displaystyle{ G\, }[/math] and expressions derived w.r.t. [math]\displaystyle{ O \, }[/math], via a coordinate transformation.

• The exciting forces [math]\displaystyle{ \mathbf{X}_1, \mathbf{X}_3 \, }[/math] are defined in an obvious manner along the X- and Z-axis. The Roll moment [math]\displaystyle{ \mathbf{X}_4 \, }[/math] is defined initially about [math]\displaystyle{ G\, }[/math].

Need to derive definitions for the coefficients that enter the Heave & Surge-Roll equations of motion:

[math]\displaystyle{ M = \rho \forall, \qquad \forall = \ }[/math] volume of water displaced by body archimedian principle of buoyancy </math> [math]\displaystyle{ C_{33} = \rho g A_\omega = \rho g B, \qquad A_\omega = }[/math] body waterplane area </math> [math]\displaystyle{ = B \, \ }[/math] (Beam in two dimensions) [math]\displaystyle{ \left( C_{44} \right)_G = \rho g \frac{B^3}{12} = \ }[/math] Roll restoring moment due to a small angular displacement about the center of gravity. Verify for all wall and non-wall sided sections [math]\displaystyle{ C_{44} \equiv \left( C_{44} \right)+G \ne \left( C_{44} \right)_O; \quad }[/math] Derive an expression for [math]\displaystyle{ \ \left( C_{44} \right)_O \ }[/math] in terms of [math]\displaystyle{ \ \left( C_{44} \right)_G. }[/math]

---

This article is based on the MIT open course notes and the original article can be found here

Ocean Wave Interaction with Ships and Offshore Energy Systems