Difference between revisions of "Introduction to KdV"
(Created page with '{{nonlinear waves course | chapter title = Introduction to KdV | next chapter = Numerical Solution of the KdV | previous chapter = Nonlinear Shallow Water Waves }} {…') |
|||
| (40 intermediate revisions by 2 users not shown) | |||
| Line 10: | Line 10: | ||
The KdV (Korteweg-De Vries) equation is one of the most important non-linear | The KdV (Korteweg-De Vries) equation is one of the most important non-linear | ||
pde's. It was originally derived to model shallow water waves with weak | pde's. It was originally derived to model shallow water waves with weak | ||
| − | nonlinearities, but it has a wide variety of applications. The KdV equation | + | nonlinearities, but it has a wide variety of applications. The derivation of |
| + | the KdV is given in [[KdV Equation Derivation]]. The KdV equation | ||
is written as | is written as | ||
<center><math> | <center><math> | ||
\partial _{t}u+6u\partial _{x}u+\partial _{x}^{3}u=0. | \partial _{t}u+6u\partial _{x}u+\partial _{x}^{3}u=0. | ||
</math></center> | </math></center> | ||
| + | |||
| + | More information about it can be found at [http://en.wikipedia.org/wiki/Korteweg%E2%80%93de_Vries_equation Korteweg de Vries equation] | ||
==Travelling Wave Solution== | ==Travelling Wave Solution== | ||
| Line 20: | Line 23: | ||
The KdV equation posesses travelling wave solutions. One particular | The KdV equation posesses travelling wave solutions. One particular | ||
travelling wave solution is called a soltion and it was discovered | travelling wave solution is called a soltion and it was discovered | ||
| − | experimentally by John Scott Russell in 1834 | + | experimentally by [http://en.wikipedia.org/wiki/John_Scott_Russell John Scott Russell] |
| − | theoretically until the work of Korteweg and | + | in 1834. However, it was not understood |
| + | theoretically until the work of [http://en.wikipedia.org/wiki/Diederik_Korteweg Korteweg] and | ||
| + | [http://en.wikipedia.org/wiki/Gustav_de_Vries de Vries] in 1895. | ||
We begin with the assumption that the wave travels with contant form, i.e. | We begin with the assumption that the wave travels with contant form, i.e. | ||
| Line 28: | Line 33: | ||
u\left( x,t\right) =f\left( x-ct\right) | u\left( x,t\right) =f\left( x-ct\right) | ||
</math></center> | </math></center> | ||
| − | Note that in this equation the parameter <math>c</math> is an unknown as | + | Note that in this equation the parameter <math>c</math> is an unknown as is the |
| − | function <math>f.</math> Only very special values of <math>c</math> and <math>f</math> will give travelling | + | function <math>f.</math> |
| − | waves. If we substitute this expression into the KdV equation we obtain | + | Only very special values of <math>c</math> and <math>f</math> will give travelling |
| + | waves. | ||
| + | We introduce the coordinate <math>\zeta = x - ct</math>. | ||
| + | If we substitute this expression into the KdV equation we obtain | ||
<center><math> | <center><math> | ||
| − | -c\frac{ | + | -c\frac{\mathrm{d}f}{\mathrm{d}\zeta}+6f\frac{\mathrm{d}f}{\mathrm{d}\zeta}+\frac{\mathrm{d}^{3}f}{\mathrm{d}\zeta^{3}}=0 |
</math></center> | </math></center> | ||
| − | We can integrate this with respect to <math> | + | We can integrate this with respect to <math>\zeta</math> to obtain |
<center><math> | <center><math> | ||
| − | -cf+3f^{2}+\frac{d^{2}f}{ | + | -cf+3f^{2}+\frac{\mathrm{d}^{2}f}{\mathrm{d}\zeta^{2}}=A_{1} |
</math></center> | </math></center> | ||
where <math>A</math> is a constant of integration. | where <math>A</math> is a constant of integration. | ||
| − | If think about this equation as Newton's second law in a potential well <math> | + | If we think about this equation as Newton's second law in a potential well <math> |
V(f) </math> then the equation is | V(f) </math> then the equation is | ||
<center><math> | <center><math> | ||
| − | \frac{d^{2}f}{ | + | \frac{\mathrm{d}^{2}f}{\mathrm{d}\zeta^{2}}= -\frac{\mathrm{d}V}{\mathrm{d}f} |
| − | |||
| − | |||
| − | |||
| − | \ | ||
</math></center> | </math></center> | ||
| − | + | then the potential well is given by | |
<center><math> | <center><math> | ||
| − | + | V\left( f\right) =-A_{0}-A_{1}f-c\frac{f^{2}}{2}+f^{3} | |
| − | |||
| − | |||
| − | |||
| − | V\left( f\right) =-A_{0}-A_{1}f-\frac{2} | ||
</math></center> | </math></center> | ||
Therefore our equation for <math>f</math> may be thought of as the motion of a particle | Therefore our equation for <math>f</math> may be thought of as the motion of a particle | ||
in a cubic well. | in a cubic well. | ||
| − | + | The constant <math>A_0</math> has no effect on our solution so we can set it to be zero. | |
| − | + | We can choose the constant <math>A_{1}=0</math> and then we have a | |
| − | We can choose the | ||
maximum at <math>f=0</math>. There is a solution which rolls from this at <math>t=-\infty </math> | maximum at <math>f=0</math>. There is a solution which rolls from this at <math>t=-\infty </math> | ||
and then runs up the other side and finally returns to the maximum at <math> | and then runs up the other side and finally returns to the maximum at <math> | ||
| Line 70: | Line 69: | ||
f^{^{\prime }}=v.</math> This gives us | f^{^{\prime }}=v.</math> This gives us | ||
<center><math>\begin{matrix} | <center><math>\begin{matrix} | ||
| − | \frac{ | + | \frac{\mathrm{d}f}{\mathrm{d}\zeta} &=&v \\ |
| − | + | \frac{\mathrm{d}v}{\mathrm{d}\zeta} &=&A_{1}+cf-3f^{2} | |
\end{matrix}</math></center> | \end{matrix}</math></center> | ||
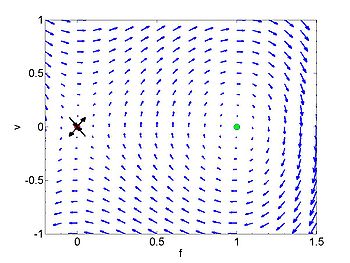
If we chose <math>A_{1}=0</math> then we obtain two equilibria at <math>(f,v)=\left( | If we chose <math>A_{1}=0</math> then we obtain two equilibria at <math>(f,v)=\left( | ||
| − | 0,0\right) <math> and < | + | 0,0\right) </math> and <math>(3/c,0).</math> If we analysis these equilibria we find the |
| − | first is a saddle and the second is | + | first is a saddle and the second is a nonlinear center (it is neither repelling nor |
| − | homoclinic connection which connects the equilibrium point at the origin. | + | attracting). |
| + | The Jacobian matrix for the saddle point is | ||
| + | <center><math> | ||
| + | J_{\left( 0,0\right) }=\left( | ||
| + | \begin{array}{cc} | ||
| + | 0 & 1 \\ | ||
| + | c & 0 | ||
| + | \end{array} | ||
| + | \right) | ||
| + | </math></center> | ||
| + | which has eigenvalues at <math>\pm \sqrt{c}</math> and the incident directions are | ||
| + | <center><math> | ||
| + | \left( | ||
| + | \begin{array}{c} | ||
| + | 1\\ | ||
| + | \sqrt{c} | ||
| + | \end{array} | ||
| + | \right) \leftrightarrow \sqrt{c},\left( | ||
| + | \begin{array}{c} | ||
| + | -1 \\ | ||
| + | \sqrt{c} | ||
| + | \end{array} | ||
| + | \right) \leftrightarrow -\sqrt{c} | ||
| + | </math></center> | ||
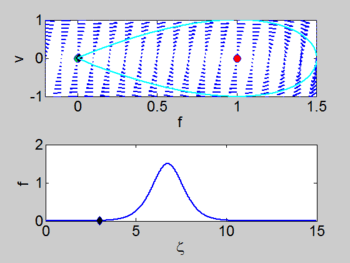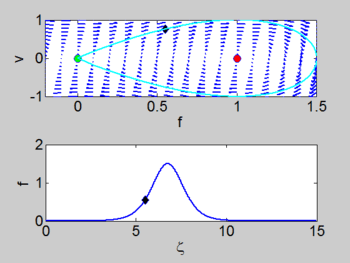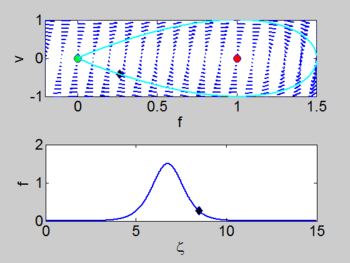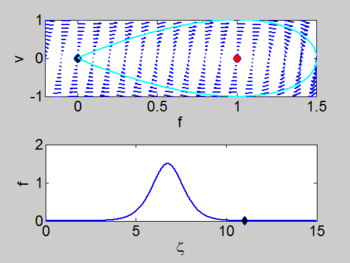
| + | There is a | ||
| + | homoclinic connection which connects the equilibrium point at the origin. This holoclinic | ||
| + | connection represents the solitary wave. Within this homoclinic connection | ||
| + | lie periodic orbits which represent the cnoidal waves. | ||
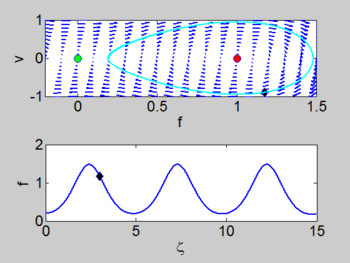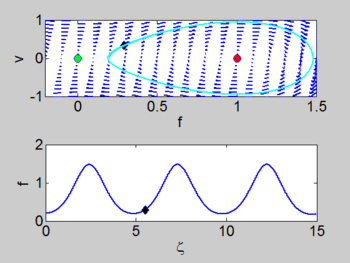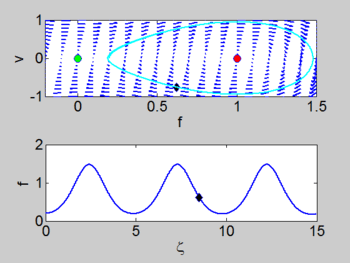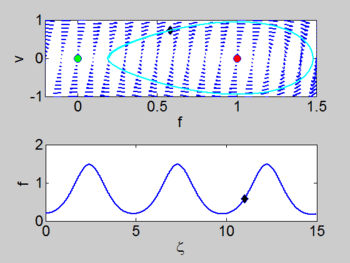
| − | = | + | {| class="wikitable" |
| + | |- | ||
| + | ! Phase portrait | ||
| + | ! Solitary Wave | ||
| + | ! Cnoidal Wave | ||
| + | |- | ||
| + | | [[Image:Kdv phase portrait.jpg|thumb|350px|Phase portrait]] | ||
| + | | [[Image:Kdv wave solitary2.gif|thumb|350px|Solitary Wave]] | ||
| + | | [[Image:Kdv wave cn.gif|thumb|350px|Cnoidal Wave]] | ||
| + | |} | ||
We can also integrate the equation | We can also integrate the equation | ||
<center><math> | <center><math> | ||
| − | -cf+3f^{2}+\frac{d^{2}f}{ | + | -cf+3f^{2}+\frac{\mathrm{d}^{2}f}{\mathrm{d}\zeta^{2}}=A_{1} |
</math></center> | </math></center> | ||
by multiplying by <math>f^{\prime }</math>and integrating. This gives us | by multiplying by <math>f^{\prime }</math>and integrating. This gives us | ||
<center><math> | <center><math> | ||
| − | \frac{\left( f^{^{\prime }}\right) ^{2}}{2}=A_{0}+A_{1}f | + | \frac{\left( f^{^{\prime }}\right) ^{2}}{2}=A_{0}+A_{1}f + c\frac{ |
| + | f^{2}}{2}-f^{3} = -V(f) | ||
</math></center> | </math></center> | ||
| − | + | It is no coincidence that the right hand side is the potential energy, because this | |
| + | is nothing more that the equation for conservation of energy (or the first | ||
| + | integral of the Lagrangian system) which does not depend on <math>\zeta</math>. | ||
| + | |||
| + | This is a separable equation and the only challenge is to integrate | ||
<center><math> | <center><math> | ||
| − | \frac{\ | + | \int \frac{1}{\sqrt{-2V(f)}} \mathrm{d}f. |
| − | |||
</math></center> | </math></center> | ||
| − | + | ||
| − | + | ==Formula for the solitary wave== | |
| + | |||
| + | We know that the solitary wave solution is found when <math> | ||
A_{0}=A_{1}=0.</math> This gives us | A_{0}=A_{1}=0.</math> This gives us | ||
<center><math> | <center><math> | ||
| Line 101: | Line 142: | ||
This can be solved by separation of variables to give | This can be solved by separation of variables to give | ||
<center><math> | <center><math> | ||
| − | \int \frac{ | + | \int \frac{\mathrm{d}f}{f\sqrt{c-2f}}=\int \mathrm{d}\zeta |
</math></center> | </math></center> | ||
We then substitute | We then substitute | ||
<center><math> | <center><math> | ||
| − | f=\frac{1}{2}c\ | + | f=\frac{1}{2}c\,\mathrm{sech}^{2}\left( s\right) |
</math></center> | </math></center> | ||
and note that | and note that | ||
<center><math> | <center><math> | ||
| − | c-2f=c\left( 1-\ | + | c-2f=c\left( 1-\mathrm{sech}^{2}\left( s\right) \right) =c\tanh ^{2}\left( f\right) |
</math></center> | </math></center> | ||
and that | and that | ||
<center><math> | <center><math> | ||
| − | \frac{ | + | \frac{\mathrm{d}f}{\mathrm{d}s}=-c\frac{\sinh \left( f\right) }{\cosh ^{3}\left( f\right) } |
</math></center> | </math></center> | ||
This means that | This means that | ||
<center><math>\begin{matrix} | <center><math>\begin{matrix} | ||
| − | \int \frac{ | + | \int \frac{\mathrm{d}f}{f\sqrt{c-2f}} &=&-\frac{2}{\sqrt{c}}\int \frac{\sinh \left( |
| − | f\right) }{\ | + | f\right) }{\mathrm{sech}^{2}\left( s\right) \tanh \left( f\right) \cosh ^{3}\left( |
| − | f\right) } | + | f\right) }\mathrm{d}s \\ |
| − | &=&-\frac{2}{\sqrt}s | + | &=&-\frac{2}{\sqrt{c}}s |
\end{matrix}</math></center> | \end{matrix}</math></center> | ||
This gives us | This gives us | ||
<center><math> | <center><math> | ||
| − | -\frac{2}{\sqrt}s= | + | -\frac{2}{\sqrt{c}}s=\zeta+a |
</math></center> | </math></center> | ||
Therefore | Therefore | ||
<center><math> | <center><math> | ||
| − | f=\frac{1}{2}c\ | + | f=\frac{1}{2}c\,\mathrm{sech}^{2}\left( \frac{\sqrt{c}}{2}\left( \zeta+a\right) \right) |
</math></center> | </math></center> | ||
Of course we assumed that <math>x=x-ct</math> so the formula for the solitary wave is | Of course we assumed that <math>x=x-ct</math> so the formula for the solitary wave is | ||
given by | given by | ||
| − | |||
<center><math> | <center><math> | ||
| − | f\left( x-ct\right) =\frac{1}{2}c\ | + | f\left( x-ct\right) =\frac{1}{2}c\,\mathrm{sech}^{2}\left[ \frac{\sqrt{c}}{2}\left( |
x-ct+a\right) \right] | x-ct+a\right) \right] | ||
</math></center> | </math></center> | ||
| − | + | Note that a solution exists for each | |
| − | the | + | <math>c</math>, and that the amplitude is proportional to <math>c.</math> All of this was |
| − | + | discovered experimentally by | |
| − | + | [http://en.wikipedia.org/wiki/John_Scott_Russell John Scott Russell]. | |
| + | |||
| + | ==Formula for the cnoidal wave== | ||
| + | |||
| + | If we consider the case when the solution oscillates between two values <math>F_2 < F_3</math> | ||
| + | (which we can assume are also roots of <math>V(f)</math> without loss of generality) then | ||
| + | we can integrate the equation to obtain | ||
<center><math> | <center><math> | ||
| − | f\left( | + | f\left( \zeta\right) =F_2+(F_3 - F_2) \mathrm{cn}^{2}\left( \gamma \zeta ;k\right) |
| − | |||
</math></center> | </math></center> | ||
| − | + | where <math>cn</math> is a Jacobi Elliptic function and | |
| − | <math> | + | <math>\gamma</math> and <math>k</math> are constants which depend on <math>c</math>. |
| − | + | Derivation of this equation is found [[KdV Cnoidal Wave Solutions]]. | |
| − | + | We can write this equation as | |
<center><math> | <center><math> | ||
| − | f\left( x-ct\right) =a+ | + | f\left( x-ct\right) =a+b \mathrm{cn}^{2}\left( \gamma (x-ct);k\right) |
</math></center> | </math></center> | ||
| − | where <math> | + | where <math>a=k^2\gamma^2</math> and <math>c = 6b + 4(2k^2 -1)\gamma^2</math>. |
| − | + | These waves are known as [http://en.wikipedia.org/wiki/Cnoidal_wave cnoidal waves]. | |
| + | |||
| + | In the limit the two solutions agree. We also obtain a sinusoidal solution in the limit of | ||
| + | small amplitude. | ||
| + | |||
| + | == Lecture Videos == | ||
| + | |||
| + | === Part 1 === | ||
| + | |||
| + | {{#ev:youtube|SzZ-KhvvPio}} | ||
| + | |||
| + | === Part 2 === | ||
| + | |||
| + | {{#ev:youtube|QltlSQQBtrs}} | ||
| + | |||
| + | === Part 3 === | ||
| + | |||
| + | {{#ev:youtube|NJ7h3Z9QtvU}} | ||
| + | |||
| + | === Part 4 === | ||
| + | |||
| + | {{#ev:youtube|NictSlSgRbM}} | ||
Latest revision as of 03:57, 10 August 2023
| Nonlinear PDE's Course | |
|---|---|
| Current Topic | Introduction to KdV |
| Next Topic | Numerical Solution of the KdV |
| Previous Topic | Nonlinear Shallow Water Waves |
The KdV (Korteweg-De Vries) equation is one of the most important non-linear pde's. It was originally derived to model shallow water waves with weak nonlinearities, but it has a wide variety of applications. The derivation of the KdV is given in KdV Equation Derivation. The KdV equation is written as
More information about it can be found at Korteweg de Vries equation
Travelling Wave Solution
The KdV equation posesses travelling wave solutions. One particular travelling wave solution is called a soltion and it was discovered experimentally by John Scott Russell in 1834. However, it was not understood theoretically until the work of Korteweg and de Vries in 1895.
We begin with the assumption that the wave travels with contant form, i.e. is of the form
Note that in this equation the parameter [math]\displaystyle{ c }[/math] is an unknown as is the function [math]\displaystyle{ f. }[/math] Only very special values of [math]\displaystyle{ c }[/math] and [math]\displaystyle{ f }[/math] will give travelling waves. We introduce the coordinate [math]\displaystyle{ \zeta = x - ct }[/math]. If we substitute this expression into the KdV equation we obtain
We can integrate this with respect to [math]\displaystyle{ \zeta }[/math] to obtain
where [math]\displaystyle{ A }[/math] is a constant of integration.
If we think about this equation as Newton's second law in a potential well [math]\displaystyle{ V(f) }[/math] then the equation is
then the potential well is given by
Therefore our equation for [math]\displaystyle{ f }[/math] may be thought of as the motion of a particle in a cubic well.
The constant [math]\displaystyle{ A_0 }[/math] has no effect on our solution so we can set it to be zero. We can choose the constant [math]\displaystyle{ A_{1}=0 }[/math] and then we have a maximum at [math]\displaystyle{ f=0 }[/math]. There is a solution which rolls from this at [math]\displaystyle{ t=-\infty }[/math] and then runs up the other side and finally returns to the maximum at [math]\displaystyle{ t=\infty . }[/math] This corresponds to a solitary wave solution.
We can also think about the equation as a first order system using [math]\displaystyle{ f^{^{\prime }}=v. }[/math] This gives us
If we chose [math]\displaystyle{ A_{1}=0 }[/math] then we obtain two equilibria at [math]\displaystyle{ (f,v)=\left( 0,0\right) }[/math] and [math]\displaystyle{ (3/c,0). }[/math] If we analysis these equilibria we find the first is a saddle and the second is a nonlinear center (it is neither repelling nor attracting). The Jacobian matrix for the saddle point is
which has eigenvalues at [math]\displaystyle{ \pm \sqrt{c} }[/math] and the incident directions are
There is a homoclinic connection which connects the equilibrium point at the origin. This holoclinic connection represents the solitary wave. Within this homoclinic connection lie periodic orbits which represent the cnoidal waves.
| Phase portrait | Solitary Wave | Cnoidal Wave |
|---|---|---|
We can also integrate the equation
by multiplying by [math]\displaystyle{ f^{\prime } }[/math]and integrating. This gives us
It is no coincidence that the right hand side is the potential energy, because this is nothing more that the equation for conservation of energy (or the first integral of the Lagrangian system) which does not depend on [math]\displaystyle{ \zeta }[/math].
This is a separable equation and the only challenge is to integrate
Formula for the solitary wave
We know that the solitary wave solution is found when [math]\displaystyle{ A_{0}=A_{1}=0. }[/math] This gives us
This can be solved by separation of variables to give
We then substitute
and note that
and that
This means that
This gives us
Therefore
Of course we assumed that [math]\displaystyle{ x=x-ct }[/math] so the formula for the solitary wave is given by
Note that a solution exists for each [math]\displaystyle{ c }[/math], and that the amplitude is proportional to [math]\displaystyle{ c. }[/math] All of this was discovered experimentally by John Scott Russell.
Formula for the cnoidal wave
If we consider the case when the solution oscillates between two values [math]\displaystyle{ F_2 \lt F_3 }[/math] (which we can assume are also roots of [math]\displaystyle{ V(f) }[/math] without loss of generality) then we can integrate the equation to obtain
where [math]\displaystyle{ cn }[/math] is a Jacobi Elliptic function and [math]\displaystyle{ \gamma }[/math] and [math]\displaystyle{ k }[/math] are constants which depend on [math]\displaystyle{ c }[/math]. Derivation of this equation is found KdV Cnoidal Wave Solutions. We can write this equation as
where [math]\displaystyle{ a=k^2\gamma^2 }[/math] and [math]\displaystyle{ c = 6b + 4(2k^2 -1)\gamma^2 }[/math]. These waves are known as cnoidal waves.
In the limit the two solutions agree. We also obtain a sinusoidal solution in the limit of small amplitude.