Waves on a Variable Beam
Introduction
We consider here the equations for a non-uniform free beam. We begin by presenting the theory for a uniform beam.<br\>
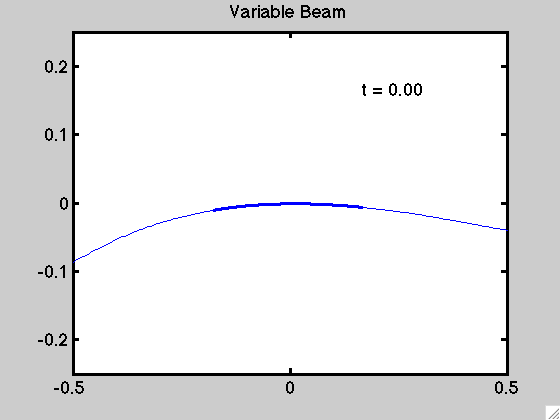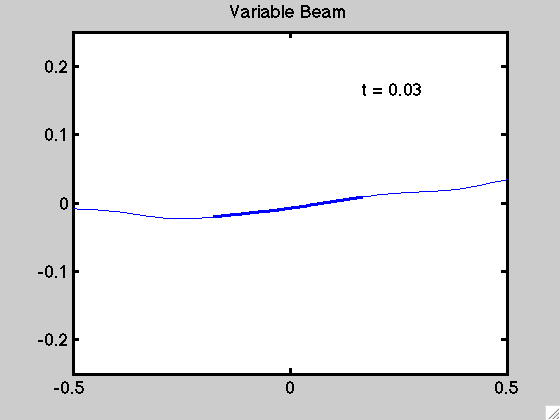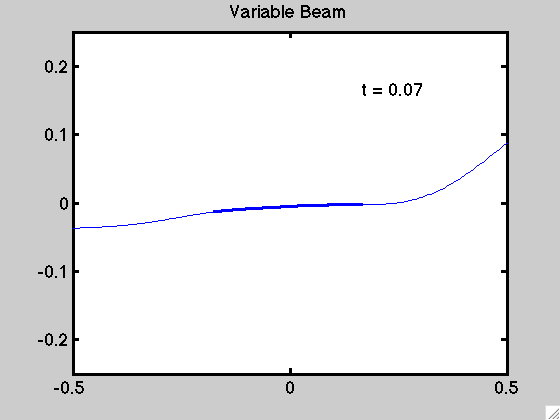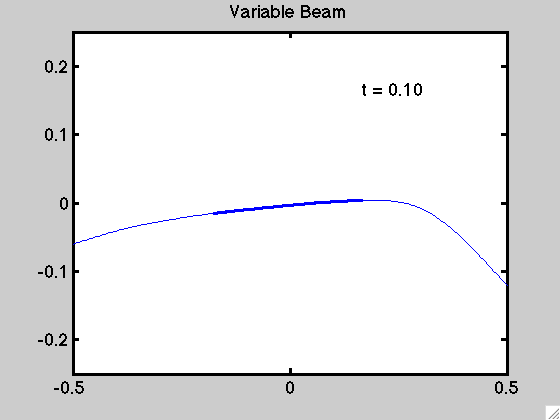
An example of the motion for a non-uniform beam is demonstrated below:
Equations for a beam
There are various beam theories that can be used to describe the motion of the beam. The simplest theory is the Bernoulli-Euler Beam theory (other beam theories include the Timoshenko Beam theory and Reddy-Bickford Beam theory where shear deformation of higher order is considered). For a Bernoulli-Euler Beam, the equation of motion is given by the following
where [math]\displaystyle{ \beta(x) }[/math] is the non dimensionalised flexural rigidity, and [math]\displaystyle{ \gamma }[/math] is non-dimensionalised linear mass density function. Note that this equations simplifies if the plate has constant properties (and that [math]\displaystyle{ h }[/math] is the thickness of the plate, [math]\displaystyle{ p }[/math] is the pressure and [math]\displaystyle{ \zeta }[/math] is the plate vertical displacement) .
The edges of the plate can satisfy a range of boundary conditions. The natural boundary condition (i.e. free-edge boundary conditions).
at the edges of the plate.
The problem is subject to the initial conditions
- [math]\displaystyle{ \zeta(x,0)=f(x) \,\! }[/math]
- [math]\displaystyle{ \partial_t \zeta(x,0)=g(x) }[/math]
Solution for a uniform beam in eigenfunctions with no pressure
If the beam is uniform the equations can be written as
We can express the deflection as the series
where [math]\displaystyle{ X_n }[/math] are the Eigenfunctions for a Uniform Free Beam and [math]\displaystyle{ k_m = \lambda^2_n \sqrt{\beta/\gamma} }[/math] where [math]\displaystyle{ \lambda_n }[/math] are the eigenfunctions.
Then [math]\displaystyle{ A_n \,\! }[/math] and [math]\displaystyle{ B_n \,\! }[/math] can be found using orthogonality properties:
- [math]\displaystyle{ A_n=\frac{\int_{-L}^{L}f(x)X_n(x)\mathrm{d}x}{\int_{-L}^{L}X_n(x)X_n(x)\mathrm{d}x} \,\! }[/math]
- [math]\displaystyle{ B_n=\frac{\int_{-L}^{L}g(x)X_n(x)\mathrm{d}x}{\int_{-L}^{L}X_n(x)X_n(x)\mathrm{d}x} }[/math]
Note that we cannot give the plate an initial velocity that contains a rigid body motions which is why the sum starts at [math]\displaystyle{ n=2 }[/math] for time derivative.
Variational Techniques
As an alternative to solving the eigenvalue problem, we can equivalently minimise the Rayleigh Quotient (Linton and McIver 2001):
where [math]\displaystyle{ \varepsilon[\zeta] \,\! }[/math] is known as the energy functional, and [math]\displaystyle{ H[\zeta] \,\! }[/math] is some constraint.
In the case of a uniform beam with zero transverse load, our energy functional is (Lanczos 1949):
If we choose
Then minimizing the Rayleigh Quotient can be expressed as a variational problem
min [math]\displaystyle{ R[\zeta]=\frac{\beta}{2}\int_{-L}^{L}\left(\frac{\partial^2 \zeta}{\partial x^2} \right)^2 \mathrm{d}x }[/math]
subject to [math]\displaystyle{ \int_{-L}^{L}\gamma \zeta^2 \mathrm{d}x=1 }[/math]which will in turn, also solve our eigenvalue problem.
Rayleigh-Ritz method
We can essentially replace the variational problem of finding a [math]\displaystyle{ y(x) \,\! }[/math] that extremises [math]\displaystyle{ J[y] \,\! }[/math] to finding a set of constants [math]\displaystyle{ a_1, a_2, ..., a_N \,\! }[/math] which extremise [math]\displaystyle{ J[a_1, a_2, ..., a_N] \,\! }[/math], through using the Rayleigh-Ritz method.
We solve
for all [math]\displaystyle{ k=1,2,...,N \,\! }[/math].
In our example of non-uniform beams, the assumption is made that we are able to approximate the eigenfunctions for a non-uniform beam as a linear combination of the eigenfunctions for a linear beam:
Solution for a Non-uniform free beam in eigenfunctions
In the case of a non-uniform free beam, the Euler-Bernoulli beam equation becomes:
Using separation of variables, where [math]\displaystyle{ \zeta(x,t)=\widehat{X}(x)\widehat{T}(t) \,\! }[/math], we obtain a corresponding eigenfunction problem (with eigenvalues denoted by [math]\displaystyle{ \mu_n=\widehat{k}_n^4 \,\! }[/math]):
which leads us to the following variational expression:
min [math]\displaystyle{ J[\widehat{X}_n]=\frac{1}{2}\int_{-L}^{L} \bigg\{\beta(x)(\widehat{X}_n^{''})^2 -\mu_n \gamma(x) \widehat{X}_n^2 \bigg\}\mathrm{d}x }[/math]
We can approximate this using Rayleigh-Ritz and obtain:
Then extremising [math]\displaystyle{ J[\vec{a}] \,\! }[/math] as follows
for all [math]\displaystyle{ k=1,2,...,N \,\! }[/math], allows us to obtain:
for all [math]\displaystyle{ k=1,2,...N \,\! }[/math] (here [math]\displaystyle{ \mu_i \,\! }[/math] denotes both the Lagrange multiplier and eigenvalues of a non-uniform beam)
Converting to Matrix Form
If we define
- [math]\displaystyle{ K_{ik}=\int_{-L}^{L}\beta(x) {X}_{i}^{''} {X}_{k}^{''}\mathrm{d}x \,\! }[/math]
- [math]\displaystyle{ M_{ik}=\int_{-L}^{L} \gamma(x){X}_{i}{X}_{k}\mathrm{d}x \,\! }[/math]
then for all [math]\displaystyle{ k=1,2,...N \,\! }[/math]:
Let us create the matrix [math]\displaystyle{ K \,\! }[/math], with elements [math]\displaystyle{ K_{ik} \,\! }[/math], the matrix [math]\displaystyle{ M \,\! }[/math], with elements [math]\displaystyle{ M_{ik} \,\! }[/math], the sparse matrix [math]\displaystyle{ \Lambda \,\! }[/math] with [math]\displaystyle{ \mu_i \,\! }[/math] terms on the diagonal, and the vector [math]\displaystyle{ \mathbf{a} \,\! }[/math]. We can consequently express the above sum in the following way:
So we can solve for [math]\displaystyle{ \mathbf{a} \,\! }[/math] in any of the problems below to obtain coefficients [math]\displaystyle{ a_i \,\! }[/math]:
- [math]\displaystyle{ (K-\Lambda M)\mathbf{a} = 0 \,\! }[/math]
- [math]\displaystyle{ K\mathbf{a}=\Lambda M\mathbf{a} \,\! }[/math]
- [math]\displaystyle{ (M^{-1}K)\mathbf{a}=\Lambda \mathbf{a} \,\! }[/math]
Quadrature
Rather than tediously evaluating an integral for each element of the matrices [math]\displaystyle{ K \,\! }[/math] and [math]\displaystyle{ M \,\! }[/math], we can break up the integral into subintervals with weights [math]\displaystyle{ w_h \,\! }[/math] using Composite Simpson's Rule:
- [math]\displaystyle{ \int_a^b f(x) dx \approx \frac{h}{3} \left[ f(x_0)+2 \sum_{j=1}^{n/2-1}f(x_{2j})+4\sum_{j=1}^{n/2}f(x_{2j-1})+f(x_n)\right] \,\! }[/math]
- [math]\displaystyle{ \approx \frac{h}{3}\left[ f(x_0)+4f(x_1)+2f(x_2)+4f(x_3)+2f(x_4)+...+4f(x_{n-1})+f(x_n)\right] \,\! }[/math]
So we can express [math]\displaystyle{ K_{ik} \,\! }[/math] as follows:
- [math]\displaystyle{ K_{ik}=\int_{-L}^{L}\beta(x) {X}_{i}^{''} {X}_{k}^{''}\mathrm{d}x \,\! }[/math]
- [math]\displaystyle{ \approx \sum \beta(x_h){X}_{i}^{''}(x_h) {X}_{k}^{''}(x_h)w_h \,\! }[/math]
- [math]\displaystyle{ \approx \vec{X}_{i}^{''} H \vec{X}_{k}^{''T} \,\! }[/math]
where
[math]\displaystyle{ H = \begin{bmatrix} \beta(x_1)w_1 & 0 & ... &0 \\ 0 & \beta(x_2)w_2 & ... &0 \\ \vdots & & \ddots&\vdots \\ 0 & ... & ...&\beta(x_h)w_h \end{bmatrix} \,\! }[/math]
and weights [math]\displaystyle{ w_h \,\! }[/math] are defined as: [math]\displaystyle{ w_1=h/3, w_2=4h/3, ... , w_h=h/3 \,\! }[/math].
We can extend this concept to the the full matrix [math]\displaystyle{ K \,\! }[/math] if we form:
where
[math]\displaystyle{ X^{''}_{mat} = \begin{bmatrix} {X}_{1}^{''}(x_1) & {X}_{1}^{''}(x_2) & ... & {X}^{''}_{1}(x_h) \\ {X}_{2}^{''}(x_1) & {X}_{2}^{''}(x_2) & ... & {X}^{''}_{2}(x_h) \\ \vdots & \vdots & & \vdots \\ {X}_{N}^{''}(x_1) & {X}_{N}^{''}(x_2) & ... & {X}^{''}_{N}(x_h) \end{bmatrix} \,\! }[/math]
For [math]\displaystyle{ M \,\! }[/math] we use an identical approach:
where
[math]\displaystyle{ J = \begin{bmatrix} \gamma(x_1)w_1 & 0 & ... &0 \\ 0 & \gamma(x_2)w_2 & ... &0 \\ \vdots & & \ddots&\vdots \\ 0 & ... & ...&\gamma(x_h)w_h \end{bmatrix} \,\! }[/math]
[math]\displaystyle{ X_{mat} = \begin{bmatrix} {X}_{1}(x_1) & {X}_{1}(x_2) & ... & {X}_{1}(x_h) \\ {X}_{2}(x_1) & {X}_{2}(x_2) & ... & {X}_{2}(x_h) \\ \vdots & \vdots & & \vdots \\ {X}_{N}(x_1) & {X}_{N}(x_2) & ... & {X}_{N}(x_h) \end{bmatrix} \,\! }[/math]
Evaluation
Using the MATLAB program eig.m, we can solve the eigenvalue problem
using the either of the commands
[Ai_values,nonuniform_eigvals] = eig(M^(-1)*K)
[Ai_values,nonuniform_eigvals] = eig(K,M)
Where the diagonal of nonuniform_eigvals denotes the eigenvalues for the nonuniform beam ([math]\displaystyle{ \mu_n \,\! }[/math]), and each column of the matrix Ai_values represents the coefficients [math]\displaystyle{ a_1, a_2,... \,\! }[/math] corresponding to [math]\displaystyle{ \widehat{X}_n \,\! }[/math]:
We can obtain the matrix [math]\displaystyle{ \widehat{X}_{mat} \,\! }[/math] by taking Xhat_mat= Ai_valuesTX_mat.
Non-uniform beam revisited
We have already solved the eigenfunction problem. We now turn our attention to the time component arising from separation of variables:
which has solutions of the form
Introducing the initial conditions
- [math]\displaystyle{ v(x,0)=f(x) \,\! }[/math]
- [math]\displaystyle{ \frac{\partial v(x,0)}{\partial t}=g(x)\,\! }[/math]
Then using the the first of these initial conditions we obtain:
multiplying by [math]\displaystyle{ m(x)\widehat{X}_n(x) \,\! }[/math] and integrating allows us to obtain:
Then using the second initial condition, and applying the same technique yields
Consequently,
where [math]\displaystyle{ \widehat{X}_0(x) \,\! }[/math] and [math]\displaystyle{ \widehat{X}_2(x) \,\! }[/math] are the two rigid modes of the non-uniform beam. Note that [math]\displaystyle{ B_0 \,\! }[/math] and [math]\displaystyle{ B_1 \,\! }[/math] do not exist.
Matlab Code
A program to solve for a variable beam can be found here variable_beam.m
Additional code
This program requires