Difference between revisions of "Category:Eigenfunction Matching Method"
| (10 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | = Introduction = | + | {{complete pages}} |
| + | |||
| + | == Introduction == | ||
A method for solving wave scattering problems in which the solution can be solve | A method for solving wave scattering problems in which the solution can be solve | ||
| Line 15: | Line 17: | ||
The method is also called the mode matching method. | The method is also called the mode matching method. | ||
| − | = Typical Problems = | + | == Typical Problems == |
There is no end to the problems which an be solved by this method, and we try to present here the solutions for some of | There is no end to the problems which an be solved by this method, and we try to present here the solutions for some of | ||
| Line 22: | Line 24: | ||
to the circular problem. | to the circular problem. | ||
| − | == Dock == | + | === Dock === |
[[Image:semiinfinite_dock.jpg|thumb|right|200px|Wave scattering by a semi-infinite dock]] | [[Image:semiinfinite_dock.jpg|thumb|right|200px|Wave scattering by a semi-infinite dock]] | ||
| Line 32: | Line 34: | ||
* [[Eigenfunction Matching for a Semi-Infinite Dock]] | * [[Eigenfunction Matching for a Semi-Infinite Dock]] | ||
* [[Eigenfunction Matching for a Finite Dock]] | * [[Eigenfunction Matching for a Finite Dock]] | ||
| + | * [[Eigenfunction Matching for a Finite Dock using Symmetry]] | ||
* [[Two Identical Docks using Symmetry]] | * [[Two Identical Docks using Symmetry]] | ||
* [[Eigenfunction Matching for a Circular Dock]] | * [[Eigenfunction Matching for a Circular Dock]] | ||
| − | + | === Submerged Dock === | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | == Submerged Dock == | ||
[[Image:submerged_inf_dock.jpg|thumb|right|200px|Wave scattering by a submerged semi-infinite dock]] | [[Image:submerged_inf_dock.jpg|thumb|right|200px|Wave scattering by a submerged semi-infinite dock]] | ||
| Line 53: | Line 51: | ||
* [[Eigenfunction Matching for a Submerged Circular Dock]] | * [[Eigenfunction Matching for a Submerged Circular Dock]] | ||
| − | + | === [[:Category:Floating Elastic Plate|Floating Elastic Plate]] === | |
| − | |||
| − | |||
| − | == [[:Category:Floating Elastic Plate|Floating Elastic Plate]] == | ||
[[Image:Semiinfinite plate.jpg|thumb|right|200px|Wave scattering by a submerged semi-infinite elastic plate]] | [[Image:Semiinfinite plate.jpg|thumb|right|200px|Wave scattering by a submerged semi-infinite elastic plate]] | ||
| Line 68: | Line 63: | ||
* [[Eigenfunction Matching Method for Floating Elastic Plates]] | * [[Eigenfunction Matching Method for Floating Elastic Plates]] | ||
* [[Eigenfunction Matching for a Circular Floating Elastic Plate]] | * [[Eigenfunction Matching for a Circular Floating Elastic Plate]] | ||
| + | |||
| + | === Submerged Rectangle === | ||
| + | |||
| + | * [[Eigenfunction Matching for a Semi-Infinite Rectangle]] | ||
| + | |||
| + | === Change in Depth === | ||
| + | |||
| + | * [[Eigenfunction Matching for a Semi-Infinite Change in Depth]] | ||
| + | * [[Eigenfunction Matching for a Finite Change in Depth]] | ||
| + | |||
| + | === Vertical Fixed Plate === | ||
| + | |||
| + | * [[Eigenfunction Matching for a Vertical Fixed Plate]] | ||
[[Category:Linear Water-Wave Theory]] | [[Category:Linear Water-Wave Theory]] | ||
[[Category:Numerical Methods]] | [[Category:Numerical Methods]] | ||
Latest revision as of 12:08, 20 June 2011
Introduction
A method for solving wave scattering problems in which the solution can be solve in various regions using separation of variables. The solution in these regions are then matched at various boundaries. The simplest problem is in Wavemaker Theory, but the separation of variables is also described in Dispersion Relation for a Free Surface
The method is described in Linton and McIver 2001. All that is required is that the domain consists of water of constant depth and that there are suitable conditions that we can separate variables. For each problem considered, the simplest case is the semi-infinite domain on one side and open water on the other, and it is this problem that we focus on in particular. The problem can then be extended to a finite domain, using Symmetry in Two Dimensions and the problem can also be extended to circular regions in three-dimensions.
The method is also called the mode matching method.
Typical Problems
There is no end to the problems which an be solved by this method, and we try to present here the solutions for some of the typical problems. As stated previously, we begin with the semi-infinite problem with open water on the left and waves incident from the left and extend this problem to the finite depth problem by Symmetry in Two Dimensions and to the circular problem.
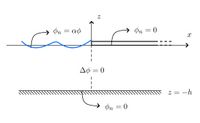
Dock
The semi-infinite problem is shown on the right.
We have the following solutions for this case.
- Eigenfunction Matching for a Semi-Infinite Dock
- Eigenfunction Matching for a Finite Dock
- Eigenfunction Matching for a Finite Dock using Symmetry
- Two Identical Docks using Symmetry
- Eigenfunction Matching for a Circular Dock
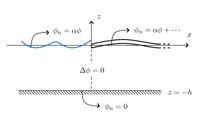
Submerged Dock
The submerged semi-infinite problem is shown on the right.
We have the following solutions for this case.
- Eigenfunction Matching for a Submerged Semi-Infinite Dock
- Eigenfunction Matching for a Submerged Finite Dock
- Two Identical Submerged Docks using Symmetry
- Eigenfunction Matching for a Submerged Circular Dock
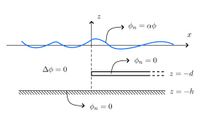
Floating Elastic Plate
The submerged semi-infinite problem is shown on the right.
We have the following solutions for this case.
- Eigenfunction Matching for a Semi-Infinite Floating Elastic Plate
- Eigenfunction Matching for a Finite Floating Elastic Plate using Symmetry
- Eigenfunction Matching Method for Floating Elastic Plates
- Eigenfunction Matching for a Circular Floating Elastic Plate
Submerged Rectangle
Change in Depth
- Eigenfunction Matching for a Semi-Infinite Change in Depth
- Eigenfunction Matching for a Finite Change in Depth
Vertical Fixed Plate
Pages in category "Eigenfunction Matching Method"
The following 22 pages are in this category, out of 22 total.
B
E
- Eigenfunction Matching for a Circular Dock
- Eigenfunction Matching for a Circular Floating Elastic Plate
- Eigenfunction Matching for a Finite Change in Depth
- Eigenfunction Matching for a Finite Dock
- Eigenfunction Matching for a Finite Dock using Symmetry
- Eigenfunction Matching for a Finite Floating Elastic Plate using Symmetry
- Eigenfunction Matching for a Finite Rectangle using Symmetry
- Eigenfunction Matching for a Semi-Infinite Change in Depth
- Eigenfunction Matching for a Semi-Infinite Dock
- Eigenfunction Matching for a Semi-Infinite Floating Elastic Plate
- Eigenfunction Matching for a Semi-Infinite Rectangle
- Eigenfunction Matching for a Submerged Circular Dock
- Eigenfunction Matching for a Submerged Finite Dock
- Eigenfunction Matching for a Submerged Semi-Infinite Dock
- Eigenfunction Matching for a Vertical Fixed Plate
- Eigenfunction Matching Method for Floating Elastic Plates